Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$. Tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(AD\). Tính khoảng cách từ điểm \(D\) đến mặt phẳng $\left( {SCN} \right)$ theo \(a\).
Trả lời bởi giáo viên
Đáp án đúng: c
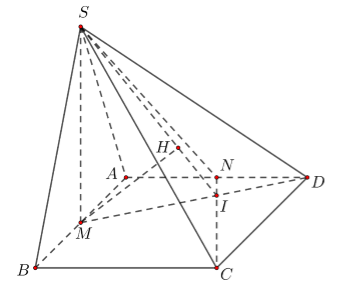
\(M\) là trung điểm của \(AB\) thì \(SM \bot \left( {ABCD} \right)\). Ta có \(SM = \dfrac{{a\sqrt 3 }}{2}\).
Gọi \(I\) là giao điểm của \(NC\) và \(MD\). Ta có \(d\left( {D;\left( {SCN} \right)} \right) = \dfrac{{ID}}{{IM}}d\left( {M;\left( {SCN} \right)} \right)\).
Vì \(ABCD\) là hình vuông nên \(NC \bot DM\) tại \(I\). \(ID.CN = DN.DC\) \( \Leftrightarrow ID = \dfrac{{DN.DC}}{{CN}} = \dfrac{{\dfrac{a}{2}.a}}{{\dfrac{{a\sqrt 5 }}{2}}} = \dfrac{{a\sqrt 5 }}{5}\) \( \Rightarrow IM = DM - ID = \dfrac{{a\sqrt 5 }}{2} - \dfrac{{a\sqrt 5 }}{5} = \dfrac{{3a\sqrt 5 }}{{10}}\) \( \Rightarrow \dfrac{{ID}}{{IM}} = \dfrac{2}{3}\).
Do \(\left\{ \begin{array}{l}IM \bot CN\\CN \bot SM\end{array} \right.\) \( \Rightarrow CN \bot \left( {SMI} \right)\). Kẻ \(MH \bot SI\), vì \(CN \bot MH\) nên \(MH \bot \left( {SCN} \right)\) \( \Rightarrow MH = d\left( {M;\left( {SCN} \right)} \right)\).
Trong tam giác \(SMI\) có \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{M{I^2}}}\) \( = \dfrac{4}{{3{a^2}}} + \dfrac{{20}}{{9{a^2}}} = \dfrac{{32}}{{9{a^2}}}\).
Vậy \(MH = \dfrac{{3a\sqrt 2 }}{8}\)\( \Rightarrow d\left( {D;\left( {SCN} \right)} \right) = \dfrac{{a\sqrt 2 }}{4}\).
Hướng dẫn giải:
Sử dụng mối quan hệ tỉ lệ giữa các khoảng cách từ các điểm đến cùng một mặt phẳng tính khoảng cách.
