Câu hỏi:
2 năm trước
Cho hình chóp tam giác đều \(S.ABC\) cạnh đáy bằng \(2a\) và chiều cao bằng \(a\sqrt 3 \). Tính khoảng cách từ tâm \(O\) của đáy \(ABC\) đến một mặt bên.
Trả lời bởi giáo viên
Đáp án đúng: c
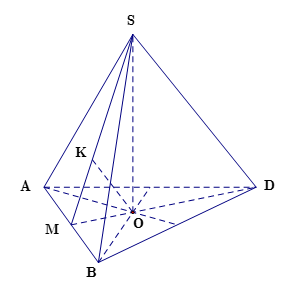
Gọi \(M\) là trung điểm \(AB\), dựng \(OK \bot SM\), ta chứng minh \(OK \bot mp\left( {SAB} \right)\).
Do \(S.ABC\) là hình chóp đều và \(O\) là tâm của đáy \(ABC\) nên \(SO \bot \left( {ABC} \right) \Rightarrow SO \bot AB\).
Do tam giác \(ABC\) đều và \(M\) là trung điểm \(AB\)nên \(AB \bot CM\).
Từ \(SO \bot AB\) và \(AB \bot CM\)suy ra \(AB \bot \left( {SCM} \right) \Rightarrow AB \bot OK\).
Từ \(OK \bot SM\) và \(AB \bot OK\)suy ra \(OK \bot mp\left( {SAB} \right)\). Bởi vậy \(d\left( {O;\left( {SAB} \right)} \right) = OK\).
Ta có \(OM = \dfrac{1}{3}CM = \dfrac{1}{3}.\dfrac{{\left( {2a} \right)\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
Trong tam giác \(SOM\) vuông tại \(O\) ta có:
\(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{S{O^2}}} = \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}} + \dfrac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} = \dfrac{{10}}{{3{a^2}}} \Rightarrow OK = a\sqrt {\dfrac{3}{{10}}} \).
Vậy \(d\left( {O;\left( {SAB} \right)} \right) = a\sqrt {\dfrac{3}{{10}}} \).
Hướng dẫn giải:
Dựng đoạn vuông góc kẻ từ \(O\) đến mặt bên, sử dụng kiến thức hình học đã biết để tính toán
