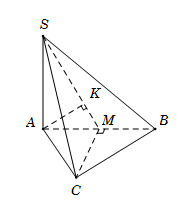
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\); \(AB = AD = 2a\), \(DC = a\). Điểm \(I\) là trung điểm đoạn \(AD\), mặt phẳng \(\left( {SIB} \right)\) và \(\left( {SIC} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Mặt phẳng \(\left( {SBC} \right)\) tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc \(60^\circ \). Tính khoảng cách từ \(D\) đến \(\left( {SBC} \right)\) theo \(a\).
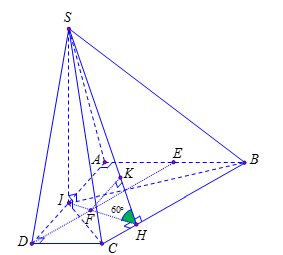
Ta có \(\left\{ \begin{array}{l}\left( {SIB} \right) \bot \left( {ABCD} \right)\\\left( {SIC} \right) \bot \left( {ABCD} \right)\\\left( {SIB} \right) \bot \left( {SIC} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\).
Trong mp\(\left( {ABCD} \right)\), kẻ \(IH \bot BC\) thì \(BC \bot \left( {SIH} \right)\) \( \Rightarrow \left( {\widehat {\left( {SBC} \right),\,\left( {ABCD} \right)}} \right) = \widehat {SHI}\).
Mặt khác:
\({S_{IBC}} = {S_{ABCD}} - {S_{ICD}} - {S_{IAB}}\) \( \Leftrightarrow {S_{IBC}} = \dfrac{1}{2}AD\left( {AB + CD} \right) - \dfrac{1}{2}ID.DC - \dfrac{1}{2}IA.AB\) \( \Leftrightarrow {S_{IBC}} = \dfrac{{3{a^2}}}{2}\).
Lại có \({S_{IBC}} = \dfrac{1}{2}IH.BC\) \( \Rightarrow IH = \dfrac{{2{S_{IBC}}}}{{BC}}\) \( \Leftrightarrow IH = \dfrac{{2{S_{IBC}}}}{{\sqrt {A{B^2} + D{E^2}} }}\)\( \Leftrightarrow IH = \dfrac{{3a}}{{\sqrt 5 }}\).
Tam giác \(SHI\) vuông tại \(I\) có \(SI = IH.\tan 60^\circ = \dfrac{{3a\sqrt 3 }}{{\sqrt 5 }}\) và \(SH = \dfrac{{6a}}{{\sqrt 5 }}\).
Gọi \(E\) là trung điểm cạnh \(AB\) và \(F\) là giao điểm của \(DF\) và \(IH\)
Vì \(BCDF\) là hình bình hành nên \(DF\,{\rm{//}}\,BC\) \( \Rightarrow d\left( {D,\,\left( {SBC} \right)} \right) = d\left( {F,\,\left( {SBC} \right)} \right) = KF\).
Hai tam giác \(DFI\) và \(DAE\) đồng dạng nên $IF = \dfrac{{DI.AE}}{{DE}} = \dfrac{a}{{\sqrt 5 }}$ \( \Rightarrow FH = \dfrac{{2a}}{{\sqrt 5 }}\).
Hai tam giác \(HKF\) và $HIS$ đồng dạng nên \(KF = \dfrac{{SI.HF}}{{SH}} = \dfrac{{a\sqrt {15} }}{5}\).
Vậy \(d\left( {D,\,\left( {SBC} \right)} \right) = \dfrac{{a\sqrt {15} }}{5}\).
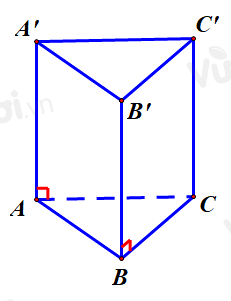
Cho hình lăng trụ đứng \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy $A B C$ là tam giác vuông cân tại \(B\) và \(AB = 4\) (tham khảo hình bên). Khoảng cách từ \(C\) đến mặt phẳng \(\left( {AB{B^\prime }{A^\prime }} \right)\) bằng
Ta có
\(\left. {\begin{array}{*{20}{l}}{CB \bot B{B^\prime }}\\{CB \bot AB}\end{array}} \right\} \Rightarrow CB \bot \left( {AB{B^\prime }{A^\prime }} \right)\)
Vậy \(d\left( {C;\left( {AB{B^\prime }{A^\prime }} \right)} \right) = CB = AB = 4\)
Đề thi THPT QG 2019 – mã đề 104
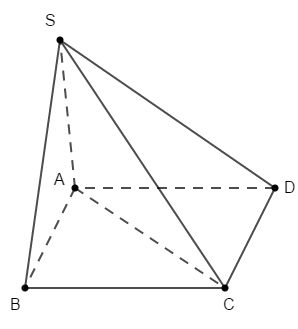
Cho hình chóp \(Oxy\) có đáy là hình vuông cạnh \(a\), mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên).
Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\) bằng
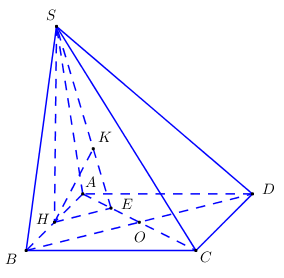
Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot AB\) (do tam giác \(SAB\) đều).
Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SH \bot AB\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\).
Ta có \(BH \cap \left( {SAC} \right) = A \Rightarrow \dfrac{{d\left( {B;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{BA}}{{HA}} = 2\) \( \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)\).
Gọi \(O = AC \cap BD\), gọi \(E\) là trung điểm của \(OA\).
Vì \(ABCD\) là hình vuông nên \(AC \bot BD\). Mà \(HE//OB \Rightarrow HE//BD\) (\(HE\) là đường trung bình của tam giác \(OAB\)) \( \Rightarrow HE \bot AC\).
Ta có \(\left\{ \begin{array}{l}AC \bot SH\,\,\left( {SH \bot \left( {ABCD} \right)} \right)\\AC \bot HE\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow AC \bot \left( {SHE} \right)\).
Trong \(\left( {SHE} \right)\) kẻ \(HK \bot SE\,\,\left( {K \in SE} \right)\) ta có \(\left\{ \begin{array}{l}HK \bot SE\\HK \bot AC\,\,\left( {AC \bot \left( {SHK} \right)} \right)\end{array} \right. \Rightarrow HK \bot \left( {SAC} \right)\).
Ta có \(HE = \dfrac{1}{2}OB = \dfrac{1}{4}BD = \dfrac{{a\sqrt 2 }}{4}\); \(SH = \dfrac{{a\sqrt 3 }}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SHE\) có: \(HK = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{4}.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {\dfrac{{2{a^2}}}{{16}} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{a\sqrt {21} }}{{14}}\).
Vậy \(d\left( {B;\left( {SAC} \right)} \right) = 2HK = \dfrac{{a\sqrt {21} }}{7}\).
Cho hình chóp tam giác đều \(S.ABC\) có \(SA = 2a,AB = 3a.\) Gọi \(M\) là trung điểm \(SC.\) Tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {SAB} \right)\).
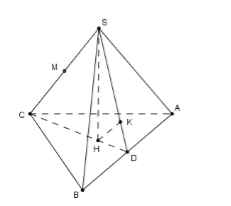
Gọi \(D\) là trung điểm của \(AB,\,\,H\) là trọng tâm tam giác \(ABC\).
Khi đó \(SH \bot \left( {ABC} \right)\) do \(S.ABC\) là hình chóp đều.
Kẻ \(HK \bot SD\) tại \(K.\)
Ta có \(\left\{ \begin{array}{l}AB \bot CD\,\,\left( {do\,\,\Delta ABC\,\,deu} \right)\\AB \bot SH\left( {do\,SH \bot \left( {ABC} \right)} \right)\end{array} \right. \Leftrightarrow AB \bot \left( {SDC} \right) \Rightarrow AB \bot HK\)
Mà \(HK \bot SD \Rightarrow HK \bot \left( {SAB} \right)\) tại \(K \Rightarrow d\left( {H,\left( {SAB} \right)} \right) = HK\)
+) Vì tam giác \(ABC\) đều cạnh \(3a\) nên
\(CD = \dfrac{{\sqrt 3 }}{2}.3a = \dfrac{{3\sqrt 3 a}}{2} \Rightarrow HD = \dfrac{1}{3}CD = \dfrac{{\sqrt 3 }}{2}a;\,\,HC = \dfrac{2}{3}CD = \sqrt 3 a\)
Vì \(S.ABC\) là chóp đều nên \(SC = SA = 2a\) .
Xét tam giác \(SHC\) vuông tại \(C,\) theo định lý Pytago ta có \(SH = \sqrt {S{C^2} - H{C^2}} = \sqrt {4{a^2} - 3{a^2}} = a\).
+) Xét tam giác \(SHD\) vuông tại \(H,\) ta có \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{D^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{\dfrac{3}{4}{a^2}}} = \dfrac{7}{{3{a^2}}} \Rightarrow HK = \dfrac{{a\sqrt {21} }}{7}\)
+) Ta có \(\dfrac{{d\left( {C,\left( {SAB} \right)} \right)}}{{d\left( {H,\left( {SAB} \right)} \right)}} = \dfrac{{CD}}{{HD}} = 3 \Leftrightarrow d\left( {C;\left( {SAB} \right)} \right) = 3.d\left( {H;\left( {SAB} \right)} \right) = \dfrac{{3a\sqrt {21} }}{7}\).
Lại có \(\dfrac{{d\left( {M,\left( {SAB} \right)} \right)}}{{d\left( {C,\left( {SAB} \right)} \right)}} = \dfrac{{MA}}{{CA}} = \dfrac{1}{2} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \dfrac{1}{2}.d\left( {C;\left( {SAB} \right)} \right) = \dfrac{{3a\sqrt {21} }}{{14}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B,\) \(AB = 4a\) và \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SAB} \right)\) bằng
Ta có: \(\left\{ \begin{array}{l}CB \bot AB\\CB \bot SA\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right)\)
Do đó \(d\left( {C,\left( {SAB} \right)} \right) = BC = AB = 4a\) (do tam giác \(ABC\) vuông cân tại \(B\))
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(\widehat {BAD} = {60^0},\,\,SA = a\) và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng \(\left( {SCD} \right)\) bằng:
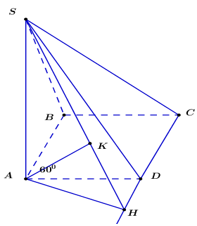
Ta có : \(AB//\left( {SCD} \right)\) \( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right) = d\)
Kẻ \(AH \bot CD;\,\,AK \bot SH\)
\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot SA\\CD \bot AH\end{array} \right. \end{array}\)
$\Rightarrow CD \bot \left( {SAH} \right) \Rightarrow CD \bot AK \Rightarrow AK \bot \left( {SCD} \right)$
$\Rightarrow d\left( {B;\;\left( {SCD} \right)} \right) = d = AK$
Xét \(\Delta AHD\) vuông tại \(H,\;\;\widehat{ADH} = {60^0}\) ta có : \(AH = AD.\sin {60^0} = \dfrac{{a\sqrt 3 }}{2}\)
Áp dụng hệ thức lượng trong \(\Delta SAH\) vuông tại \(A\) có đường cao \(AK\) ta có :
\(AK = \dfrac{{SA.AH}}{{\sqrt {S{A^2} + A{H^2}} }} = \dfrac{{a.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + \dfrac{{3{a^2}}}{4}} }} \)\(= \dfrac{{a\sqrt {21} }}{7} = d\)
Đề thi THPT QG - 2021 - mã 101
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B\),\(AB = 2a\) và \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(C\)đến mặt phẳng \((SAB)\)bằng
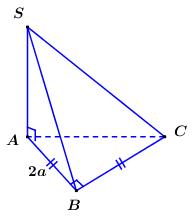
Nhận thấy \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\,\,\left( {do\,\,SA \bot \left( {ABC} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\).
\( \Rightarrow d\left( {C;\left( {SAB} \right)} \right) = BC\).
Mà \(\Delta ABC\) là tam giác vuông cân tại \(B\) \( \Rightarrow BC = AB = 2a\).
\( \Rightarrow d\left( {C;\left( {SAB} \right)} \right) = 2a\).
Gọi \({\rm{E}}\) là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng DE và SC.
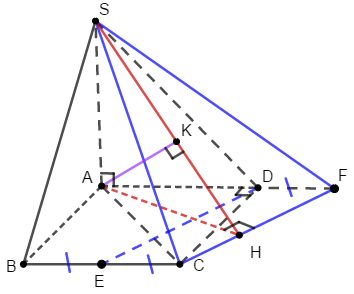
Bước 1:
Kẻ CF||DE ( F thuộc AD).
=> DE||(SCF)
Bước 2:
=>d(DE,SC)=d(DE,(SCF))=d(D,(SCF)).
ECFD là hình bình hành nên
\(\begin{array}{l}DF = EC = \dfrac{{AD}}{2} \Rightarrow \dfrac{{AF}}{{DF}} = 3\\ \Rightarrow d\left( {D,\left( {SCF} \right)} \right) = \dfrac{1}{3}d\left( {A,\left( {SCF} \right)} \right)\end{array}\).
Bước 3:
Kẻ \(AH \bot CF;AK \bot SH\)
\(\begin{array}{l}\left. \begin{array}{l} \Rightarrow CF \bot AH\\CF \bot SA\end{array} \right\} \Rightarrow CF \bot \left( {SAH} \right)\\ \Rightarrow CF \bot AK \Rightarrow AK \bot \left( {SCF} \right)\\ \Rightarrow d\left( {A,\left( {SCF} \right)} \right) = AK\end{array}\)
Bước 4:
\(\begin{array}{l}\tan \widehat {HFA} = \tan \widehat {CFD} = \dfrac{{DC}}{{DF}} = 2\\ \Rightarrow AH = 2HF\\ \Rightarrow A{H^2} + \dfrac{{A{H^2}}}{4} = A{F^2} = {\left( {\dfrac{3}{2}.a\sqrt 2 } \right)^2}\\ \Rightarrow \dfrac{5}{4}A{H^2} = \dfrac{{9{a^2}}}{2} \Rightarrow A{H^2} = \dfrac{{18{a^2}}}{5}\\\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{S{A^2}}}\\ = \dfrac{5}{{18{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{19}}{{36{a^2}}}\\ \Rightarrow AK = \dfrac{{6a}}{{\sqrt {19} }}\\ \Rightarrow d\left( {SC,DE} \right) = \dfrac{{2a}}{{\sqrt {19} }}\end{array}\)
Tính góc giữa SC và mặt phẳng \((ABCD)\).
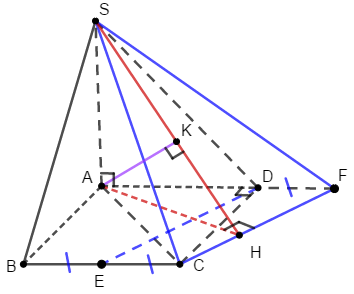
Bước 1:
\(SA \bot \left( {ABCD} \right)\) nên AC là hình chiếu của SC lên (ABCD).
Bước 2:
Góc giữa SC và (ABCD) bằng góc giữa SC và AC và bằng \(\widehat {SCA}\)
Bước 3:
\(AC = a\sqrt 2 .\sqrt 2 = 2a\)
\(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = 1 \Rightarrow \widehat {SCA} = 45^\circ \)
Vậy góc giữa SC và (ABCD) là \(45^\circ \)
Cho hình lập phương \(ABCD.MNPQ\) cạnh bằng \(a.\) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \((CNQ).\)
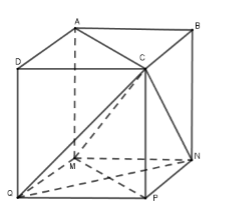
Gắn hệ trục tọa độ với \(M \equiv O;\,MN \equiv Ox;\,MA \equiv Oy;\,MQ \equiv Oz\)
Coi hình lập phương cạnh bằng \(1.\) Khi đó ta có \(M\left( {0;0;0} \right);\,N\left( {1;0;0} \right);A\left( {0;1;0} \right);Q\left( {0;0;1} \right);C\left( {1;1;1} \right)\)
Ta có \(\overrightarrow {NC} = \left( {0;1;1} \right);\,\overrightarrow {NQ} = \left( { - 1;0;1} \right) \Rightarrow \left[ {\overrightarrow {NC} ;\overrightarrow {NQ} } \right] = \left( {1; - 1;1} \right)\)
Mặt phẳng \(\left( {CNQ} \right)\) đi qua \(C;N;Q\) nên nhận \(\overrightarrow n = \left[ {\overrightarrow {NC} ;\overrightarrow {NQ} } \right] = \left( {1; - 1;1} \right)\) làm 1 VTPT.
Phương trình \(\left( {CNQ} \right):1\left( {x - 1} \right) - y + z = 0 \Leftrightarrow x - y + z - 1 = 0\)
Khoảng cách cần tìm là \(d\left( {A;\left( {CNQ} \right)} \right) = \dfrac{{\left| {0 - 1 + 0 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \dfrac{{2\sqrt 3 }}{3}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\) và \(SA = 2a\) (tham khảo hình vẽ dưới)
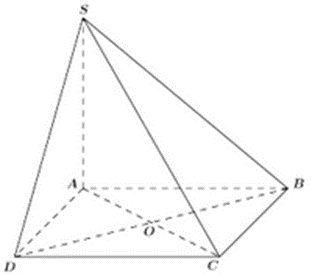
Khoảng cách từ điểm A đến mặt phẳng \(\left( {SBD} \right)\) bằng
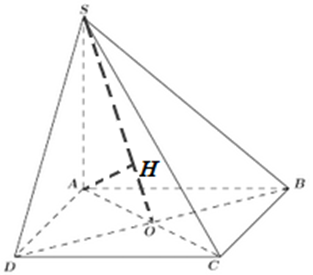
Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).
Trong \(\left( {SAC} \right)\) kẻ \(AH \bot SO\,\,\left( {H \in SO} \right)\) ta có: \(\left\{ \begin{array}{l}AH \bot SO\\AH \bot BD\end{array} \right. \Rightarrow AH \bot \left( {SBD} \right)\)\( \Rightarrow d\left( {A,\left( {SBD} \right)} \right) = AH\).
Vì ABCD là hình vuông cạnh a nên \(AO = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác vuông SAO có: \(AH = \dfrac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \dfrac{{2a.\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \dfrac{{{a^2}}}{2}} }} \)\(= \dfrac{{2a}}{3}\).
Vậy \(d\left( {A,\left( {SBD} \right)} \right) = \dfrac{{2a}}{3}\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\),\(SA = BC = {\rm{ }}a,{\rm{ }}AC = 2a\). Khoảng cách từ điểm A đến mặt phẳng (SBC) là
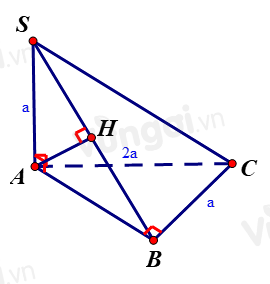
Bước 1: Kẻ AH vuông góc với SB. Chứng minh \(AH = d\left( {A,\left( {SBC} \right)} \right)\)
Kẻ AH vuông góc với SB.
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) = > SA \bot BC\\BC \bot AB\end{array} \right\}\\ \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\\AH \bot SB\\ \Rightarrow AH \bot \left( {SBC} \right)\end{array}\)
\( \Rightarrow AH = d\left( {A,\left( {SBC} \right)} \right)\)
Bước 2: Tính AH
Xét tam giác vuông ABC có: \(AB = \sqrt {A{C^2} - B{C^2}} = a\sqrt 3 \)
Xét tam giác vuông SAB có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}}\) \( = \dfrac{1}{{{a^2}}} + \dfrac{1}{{3{a^2}}} = \dfrac{4}{{3{a^2}}}\)
\( \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\)
Cho hình chóp \(S.ABCD\)có \(SA \bot \left( {ABCD} \right)\)), đáy\(ABCD\) là hình chữ nhật. Biết\(SA = a,\)\(AD = 2a,\)\(AB = a\sqrt 3 \,.\) Khoảng cách từ điểm \(B\) đến mặt phẳng\(\left( {SCD} \right)\) bằng
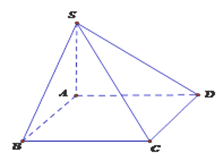
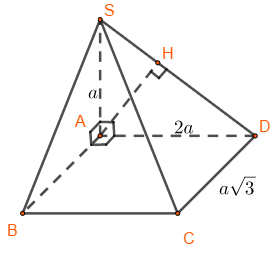
Bước 1:
Kẻ \(AH \bot SD\)
\(\left. \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right)\)
\( \Rightarrow CD \bot AH\)
Mà \(AH \bot SD\) nên \(AH \bot \left( {SCD} \right)\)
\( \Rightarrow AH = d\left( {A,\left( {SCD} \right)} \right)\)
\(AB//CD \Rightarrow AB//\left( {SCD} \right)\)
Bước 2:
\( \Rightarrow d\left( {B,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right) = AH\)
Bước 3:
Xét tam giác vuông SAD có đường cao AH, ta có:
\(\begin{array}{l}\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}}\\ = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}}\\ \Rightarrow AH = \dfrac{{2a\sqrt 5 }}{5}\end{array}\)
Đề thi THPT QG - 2021 - mã 102
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(C,\,\,\,AC = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\) bằng
Ta có: \(\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right)\)
Suy ra \(d\left( {B,\left( {SAC} \right)} \right) = BC = 3a\)
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác cạnh $BC = a,\,\,AC = 2a\sqrt 2 $, góc $\widehat {ACB} = {45^0}$. Cạnh bên $SB$ vuông góc với mặt phẳng $(ABC).$ Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBC).$
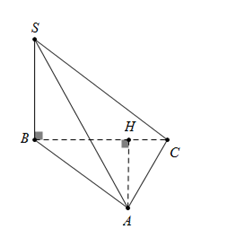
Từ A kẻ AH vuông góc với $BC,\,\,H \in BC$ (1)
Ta có $SB$ vuông góc với $\left( {ABC} \right)$$ \Rightarrow SB \bot AH\,\,\,\left( 2 \right)$
Từ (1), (2) suy ra $AH \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH.$
Tam giác $AHC$ vuông tại $H$, có $\sin \widehat {HCA} = \dfrac{{AH}}{{AC}}$.
$ \Rightarrow AH = \sin \widehat {HAC}.AC = \sin {45^0}.AC = 2a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = 2a.$
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có $AB = a\sqrt 2 $. Cạnh bên \(SA = 2a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Tính khoảng cách \(d\) từ \(D\) đến mặt phẳng \(\left( {SBC} \right)\).
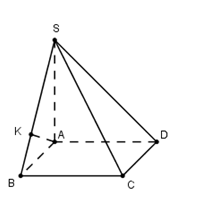
Do AD // BC nên $d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right).$
Gọi K là hình chiếu của A trên SB, suy ra $AK \bot SB\,\,\,\left( 1 \right)$.
Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBC} \right)\)
Khi $d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2a\sqrt 3 }}{3}.$
Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại \(A\) và \(B\), \(AD = a,\) \(AB = 2a,\) \(BC = 3a,\) \(SA = 2a\), \(H\) là trung điểm cạnh \(AB\), \(SH\) là đường cao của hình chóp \(S.ABCD\). Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
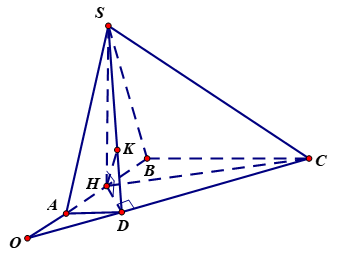
Ta có \(SH = a\sqrt 3 ;\)\(HC = a\sqrt {10} ;\) \(HD = a\sqrt 2 ;\) \(DC = a\sqrt 8 \) \( \Rightarrow H{C^2} = H{D^2} + D{C^2}\)
Vậy tam giác \(HDC\) vuông tại \(D\).
Gọi \(M\) là trung điểm của \(CD\).
Ta có: \(\dfrac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{OA}}{{OH}} = \dfrac{{AD}}{{HM}} = \dfrac{{2AD}}{{AD + BC}} = \dfrac{1}{2} \)
\(\Rightarrow d\left( {A;\left( {SCD} \right)} \right) = \dfrac{1}{2}.d\left( {H;\left( {SCD} \right)} \right) = \dfrac{1}{2}.HK\)
Trong đó \(K\) là hình chiếu vuông góc của \(H \) lên \(SD\). Ta có:
\(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{H{D^2}}} + \dfrac{1}{{H{S^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{1}{{3{a^2}}} = \dfrac{5}{{6{a^2}}}\)
\( \Rightarrow HK = \dfrac{{a\sqrt 6 }}{{\sqrt 5 }} \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 6 }}{{2\sqrt 5 }} = \dfrac{{a\sqrt {30} }}{{10}}\).
Cho hình chóp $S.ABCD$ có đáy \(ABCD\) là hình vuông cạnh bằng $a$. Cạnh bên $SA$ vuông góc với đáy, $SB$ hợp với mặt đáy một góc $60^\circ $. Tính khoảng cách \(d\) từ điểm $D$ đến mặt phẳng $\left( {SBC} \right)$.
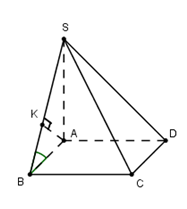
Xác định
\({60^0} = \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} \Rightarrow SA = AB.\tan \widehat {SBA} = a\sqrt 3 \).
Ta có \(AD\parallel BC \Rightarrow AD\parallel \left( {SBC} \right) \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\)
Kẻ \(AK \bot SB\,\,\,\,\left( 1 \right)\).
Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBC} \right)\)
Khi đó \(d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{a\sqrt 3 }}{2}.\)
Vậy \(d\left( {D;\left( {SBC} \right)} \right) = AK = \dfrac{{a\sqrt 3 }}{2}.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh \(a.\) Cạnh bên \(SA = \dfrac{{a\sqrt {15} }}{2}\) và vuông góc với mặt đáy \(\left( {ABCD} \right).\) Tính khoảng cách \(d\) từ \(O\) đến mặt phẳng \(\left( {SBC} \right).\)
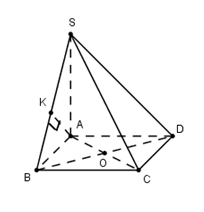
Ta có : \(OA \cap \left( {SBC} \right) = C \Rightarrow \dfrac{{d\left( {O;\left( {SBC} \right)} \right)}}{{d\left( {A;\left( {SBC} \right)} \right)}} = \dfrac{{OC}}{{AC}} = \dfrac{1}{2}\)
Do đó $d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right).$
Gọi $K$ là hình chiếu của $A$ trên $SB$$ \Rightarrow $$AK \bot SB\,\,\,\left( 1 \right)$.
Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AK\)
Tam giác vuông SAB, có $AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{a\sqrt {285} }}{{19}}.$
Vậy $d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}AK = \dfrac{{a\sqrt {285} }}{{38}}.$
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$; góc giữa đường thẳng $SB$ và mặt phẳng $\left( {ABC} \right)$ bằng ${60^0}$. Gọi $M$ là trung điểm của cạnh $AB$. Tính khoảng cách \(d\) từ $B$ đến mặt phẳng $\left( {SMC} \right)$.
\({60^0} = \widehat {\left( {SB;\left( {ABC} \right)} \right)} \)
\(= \widehat {\left( {SB;AB} \right)} = \widehat {SBA};\)
\(SA = AB.\tan \widehat {SBA} = a.\sqrt 3 = a\sqrt 3 .\)
Do $M$ là trung điểm của cạnh $AB$ nên \(d\left( {B;\left( {SMC} \right)} \right) = d\left( {A;\left( {SMC} \right)} \right)\).
Trong $(SAB)$ kẻ \(AK \bot SM\,\,\,\left( 1 \right)\).
Ta có : \(\left\{ \begin{array}{l}CM \bot AB\\CM \bot SA\end{array} \right. \Rightarrow CM \bot \left( {SAB} \right) \Rightarrow CM \bot AK\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SCM} \right) \Rightarrow d\left( {A;\left( {SMC} \right)} \right) = AK.\)
Tam giác vuông \(SAM\), có \(AK = \dfrac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \dfrac{{a\sqrt {39} }}{{13}}\).
Vậy \(d\left( {B;\left( {SMC} \right)} \right) = AK = \dfrac{{a\sqrt {39} }}{{13}}\).