Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Cạnh bên $SA = a\sqrt 3 $ và vuông góc với mặt đáy $\left( {ABC} \right)$. Tính khoảng cách $d$ từ $A$ đến mặt phẳng $\left( {SBC} \right)$.
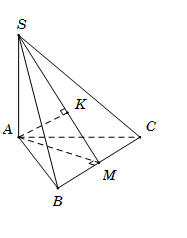
Gọi M là trung điểm BC, suy ra $AM \bot BC$ và $AM = \dfrac{{a\sqrt 3 }}{2}$.
Gọi K là hình chiếu của A trên SM, suy ra $AK \bot SM$. $\left( 1 \right)$
Ta có $\left\{ \begin{array}{l}AM \bot BC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot AK.$ $\left( 2 \right)$
Từ (1) và (2), suy ra $AK \bot \left( {SBC} \right)$ nên $d\left( {A;\left( {SBC} \right)} \right) = AK.$
Trong $\Delta \,SAM$, có $AK = \dfrac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \dfrac{{3a}}{{\sqrt {15} }} = \dfrac{{a\sqrt {15} }}{5}.$
Vậy $d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{a\sqrt {15} }}{5}.$
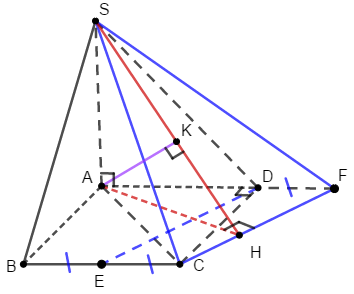
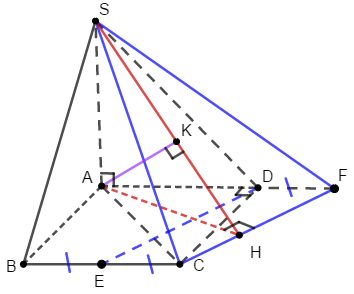
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB = a,{\rm{ }}AC = a\sqrt 3 $. Tam giác $SBC$ đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $\left( {SAC} \right)$.
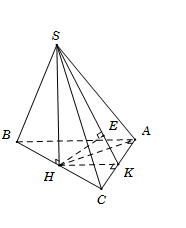
Gọi $H$ là trung điểm của $BC,$ suy ra $SH \bot BC \Rightarrow SH \bot \left( {ABC} \right)$.
Gọi $K$ là trung điểm $AC$, suy ra $HK \bot AC$.
Kẻ $HE \bot SK\,\,\,\,\left( {E \in SK} \right).\,\,\,\,\,\,\,\,\left( 1 \right)$
Ta có:\(\left\{ \begin{array}{l}AC \bot HK\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHK} \right) \Rightarrow AC \bot HE\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow HE \bot \left( {SAC} \right) \Rightarrow HE = d\left( {H;\left( {SAC} \right)} \right)\)
Ta có :
\(BH \cap \left( {SAC} \right) = C \Rightarrow \dfrac{{d\left( {B;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{BC}}{{HC}} = 2 \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right) = 2HE\)
Tam giác \(ABC\) vuông tại \(A\) nên \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{a^2} + 3{a^2}} = 2a\)
Tam giác \(SBC\) đều cạnh \(2a\) nên đường cao \(SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)
Lại có \(HK\) là đường trung bình của tam giác \(ABC\) nên \(HK = \dfrac{1}{2}AB = \dfrac{a}{2}\)
Vậy \(d\left( {B;\left( {SAC} \right)} \right) = 2HE = \dfrac{{SH.HK}}{{\sqrt {S{H^2} + H{K^2}} }} = \dfrac{{2a\sqrt {39} }}{{13}}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, các cạnh bên của hình chóp bằng nhau và bằng $2a$. Tính khoảng cách $d$ từ $A$ đến mặt phẳng $\left( SCD \right)$
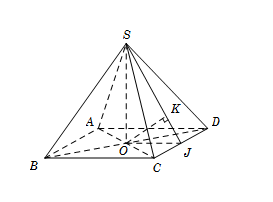
Gọi $O$ là tâm của đáy, suy ra $SO \bot \left( {ABCD} \right)$.
Ta có
\(\begin{array}{l}AO \cap \left( {SCD} \right) = C \Rightarrow \dfrac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \dfrac{{AC}}{{OC}} = 2\\ \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right).\end{array}\)
Gọi $J$ là trung điểm $CD$, suy ra $OJ \bot CD$.
Gọi $K$ là hình chiếu của $O$ trên $SJ$, suy ra $OK \bot SJ\,\,\,\left( 1 \right)$.
Ta có \(\left\{ \begin{array}{l}CD \bot OJ\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOJ} \right) \Rightarrow CD \bot OK\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow OK \bot \left( {SCD} \right) \Rightarrow d\left( {O;\left( {SCD} \right)} \right) = OK=\dfrac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }}\)
Ta có : \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {4{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{a\sqrt {14} }}{2} \Rightarrow OK = \dfrac{{\dfrac{{a\sqrt {14} }}{2}.\dfrac{a}{2}}}{{\sqrt {{{\left( {\dfrac{{a\sqrt {14} }}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} }} = \dfrac{{a\sqrt 7 }}{{\sqrt {30} }}\)
Vậy $d\left( {A;\left( {SCD} \right)} \right) = 2.OK = \dfrac{{2a\sqrt 7 }}{{\sqrt {30} }}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $1$. Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy $\left( {ABCD} \right)$. Tính khoảng cách $d$ từ $A$ đến $\left( {SCD} \right)$.
Gọi $H$ là trung điểm $AB$, suy ra $SH \bot AB \Rightarrow $$SH \bot \left( {ABCD} \right).$
Gọi $E$ là trung điểm $CD$; $K$ là hình chiếu vuông góc của $H$ trên $SE$.
Ta có : \(HE \bot CD,SH \bot CD \Rightarrow CD \bot \left( {SHE} \right)\) \( \Rightarrow CD \bot HK\), mà \(HK \bot SE\) nên \(HK \bot \left( {SCD} \right)\)
Do $AH$//$CD$ nên $d\left( {A;\left( {SCD} \right)} \right) = d\left( {H;\left( {SCD} \right)} \right).$
Khi đó $d\left( {H;\left( {SCD} \right)} \right) = HK = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }}.$
Vậy $d\left( {A;\left( {SCD} \right)} \right) = HK = \dfrac{{\sqrt {21} }}{7}.$
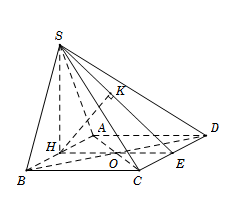
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $1$, cạnh bên hợp với mặt đáy một góc ${60^0}$. Tính khoảng cách \(d\) từ $O$ đến mặt phẳng $\left( {SBC} \right)$.

Gọi $O$ là tâm hình vuông $ABCD$ ta có \(SO \bot \left( {ABCD} \right)\)
$OB = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2},OM = \dfrac{1}{2}AB = \dfrac{a}{2}$
Xác định ${60^0}{\rm{ = }}\widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;OB} \right)} = \widehat {SBO}$ và
\(SO = OB.\tan \widehat {SBO} = \dfrac{{\sqrt 6 }}{2}\).
Gọi \(M\) là trung điểm \(BC\), kẻ \(OK \bot SM\,\,\,\,\,\left( 1 \right)\).
Ta có : \(\left\{ \begin{array}{l}BC \bot OM\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right) \Rightarrow BC \bot OK\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow OK \bot \left( {SBC} \right) \Rightarrow d\left( {O;\left( {SBC} \right)} \right) = OK\).
Tam giác vuông $SOM,$ có \(OK = \dfrac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }} = \dfrac{{\sqrt {42} }}{{14}}.\)
Vậy \(d\left( {O;\left( {SBC} \right)} \right) = OK = \dfrac{{\sqrt {42} }}{{14}}.\)
Cho hình chóp \(S.ACBD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\). Cạnh bên \(SA\) vuông góc với đáy, \(SA = AB = BC = 1\), \(AD = 2\). Tính khoảng cách \(d\) từ điểm \(A\) đến mặt phẳng \(\left( {SBD} \right)\).
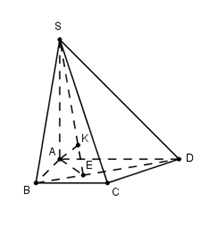
Trong (ABCD) kẻ \(AE \bot BD\), trong (SAE) kẻ \(AK \bot SE\,\,\,\,\left( 1 \right)\).
Ta có: \(\left\{ \begin{array}{l}BD \bot AE\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAE} \right) \Rightarrow BD \bot AK\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBD} \right) \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AK.\)
Tam giác vuông \(ABD\), có \(AE = \dfrac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \dfrac{{2\sqrt 5 }}{5}\).
Tam giác vuông $SAE$, có $AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{2}{3}$.
Vậy \(d\left( {A;\left( {SBD} \right)} \right) = AK = \dfrac{2}{3}\).
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và cạnh bên bằng $\dfrac{{a\sqrt {21} }}{6}$. Tính khoảng cách \(d\) từ đỉnh $A$ đến mặt phẳng $\left( {SBC} \right)$ .
Gọi \(O\) là tâm của tam giác đều \(ABC\).
Do hình chóp $S.ABC$ đều nên suy ra \(SO \bot \left( {ABC} \right)\).
Gọi \(E\) là trung điểm \(BC\) ta có:
$\begin{array}{l}AO \cap \left( {SBC} \right) = E \Rightarrow \dfrac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {O;\left( {SBC} \right)} \right)}} = \dfrac{{AE}}{{OE}} = 3\\ \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 3.d\left( {O;\left( {SBC} \right)} \right).\end{array}$
Trong $(SAE)$ kẻ \(OK \bot SE\,\,\,\,\left( 1 \right)\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AE\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot OK\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow OK \bot \left( {SBC} \right) \Rightarrow d\left( {O;\left( {SBC} \right)} \right) = OK\)
Tính được $SO = \sqrt {S{A^2} - {{\left( {\dfrac{2}{3}AE} \right)}^2}} = \sqrt {\dfrac{{21{a^2}}}{{36}} - {{\left( {\dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2}} \right)}^2}} = \dfrac{a}{2}$ và \(OE = \dfrac{1}{3}AE = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}.\)
Tam giác vuông \(SOE\), có \(OK = \dfrac{{SO.OE}}{{\sqrt {S{O^2} + O{E^2}} }} = \dfrac{a}{4}\).
Vậy $d\left( {A;\left( {SBC} \right)} \right) = 3OK = \dfrac{{3a}}{4}$.
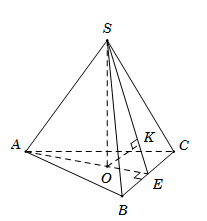
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), $AD = 2BC,$ $AB = BC = a\sqrt 3 $. Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(E\) là trung điểm của cạnh \(SC\). Tính khoảng cách \(d\) từ điểm \(E\) đến mặt phẳng \(\left( {SAD} \right)\).
Ta có
\(\begin{array}{l}EC \cap \left( {SAD} \right) = S \Rightarrow \dfrac{{d\left( {E;\left( {SAD} \right)} \right)}}{{d\left( {C;\left( {SAD} \right)} \right)}} = \dfrac{{ES}}{{CS}} = \dfrac{1}{2}\\ \Rightarrow d\left( {E;\left( {SAD} \right)} \right) = \dfrac{1}{2}d\left( {C;\left( {SAD} \right)} \right)\end{array}\).
Gọi M là trung điểm AM, suy ra ABCM là hình vuông \( \Rightarrow CM \bot AD\).
Do \(\left\{ \begin{array}{l}CM \bot AD\\CM \bot SA\end{array} \right. \Rightarrow CM \bot \left( {SAD} \right) \Rightarrow d\left( {C;\left( {SAD} \right)} \right) = CM = AB = a\sqrt 3 \)
Vậy \(d\left( {E;\left( {SAD} \right)} \right) = \dfrac{1}{2}CM = \dfrac{{a\sqrt 3 }}{2}.\)
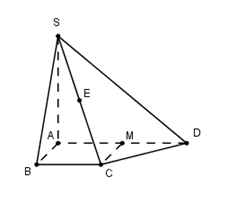
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a,{\rm{ }}AD = 2a\). Cạnh bên \(SA\) vuông góc với đáy, góc giữa \(SD\) với đáy bằng \({60^0}.\) Tính khoảng cách \(d\) từ điểm \(C\) đến mặt phẳng \(\left( {SBD} \right)\) theo \(a\).
Xác định \({60^0} = \widehat {\left( {SD,\left( {ABCD} \right)} \right)} = \widehat {\left( {SD,AD} \right)} = \widehat {SDA}\) và \(SA = AD.\tan \widehat {SDA} = 2a\sqrt 3 \).
Gọi $O$ là tâm hình chữ nhật $ABCD$ ta có
$\begin{array}{l}CA \cap \left( {SBD} \right) = O\\ \Rightarrow \dfrac{{d\left( {C;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \dfrac{{CO}}{{AO}} = 1\\ \Rightarrow d\left( {C;\left( {SBD} \right)} \right) = d\left( {A;\left( {SBD} \right)} \right)\end{array}$.
Trong $(ABCD)$ kẻ \(AE \bot BD\) và trong $(SAE)$ kẻ \(AK \bot SE\,\,\,\left( 1 \right)\).
Ta có: \(\left\{ \begin{array}{l}BD \bot AE\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAE} \right) \Rightarrow BD \bot AK\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBD} \right) \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AK\).
Tam giác vuông \(BAD\), có \(AE = \dfrac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}\).
Tam giác vuông \(SAE\), có \(AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{a\sqrt 3 }}{2}\).
Vậy $d\left( {C;\left( {SBD} \right)} \right) = AK = \dfrac{{a\sqrt 3 }}{2}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AC = 2a,{\rm{ }}BC = a$. Đỉnh $S$ cách
đều các điểm $A,{\rm{ }}B,{\rm{ }}C$. Tính khoảng cách \(d\) từ trung điểm $M$ của $SC$ đến mặt phẳng $\left( {SBD} \right)$.
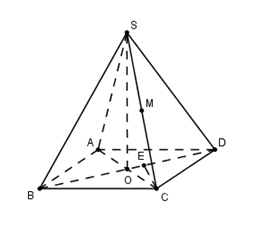
Gọi \(O\) là trung điểm \(AC\), suy ra \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). (Do tam giác $ABC$ vuông tại $B$).
Do đỉnh $S$ cách đều các điểm $A,{\rm{ }}B,{\rm{ }}C$ nên $SO \bot \left( {ABCD} \right)$.
Ta có
$\begin{array}{l}MC \cap \left( {SBD} \right) = S \Rightarrow \dfrac{{d\left( {M;\left( {SBD} \right)} \right)}}{{d\left( {C;\left( {SBD} \right)} \right)}} = \dfrac{{MS}}{{CS}} = \dfrac{1}{2}\\ \Rightarrow d\left( {M;\left( {SBD} \right)} \right) = \dfrac{1}{2}d\left( {C;\left( {SBD} \right)} \right)\end{array}$.
Kẻ \(CE \bot BD\) ta có: \(\left\{ \begin{array}{l}CE \bot BD\\CE \bot SO\end{array} \right. \Rightarrow CE \bot \left( {SBD} \right) \Rightarrow d\left( {C;\left( {SBD} \right)} \right) = CE = \dfrac{{CB.CD}}{{\sqrt {C{B^2} + C{D^2}} }} = \dfrac{{a\sqrt 3 }}{2}.\)
Vậy \(d\left( {M;\left( {SBD} \right)} \right) = \dfrac{1}{2}CE = \dfrac{{a\sqrt 3 }}{4}\).
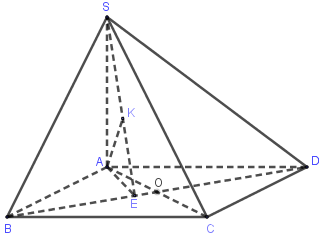
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\). Tam giác \(ABC\) đều, hình chiếu vuông góc \(H\) của đỉnh \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) trùng với trọng tâm của tam giác \(ABC\). Đường thẳng \(SD\) hợp với mặt phẳng \(\left( {ABCD} \right)\) góc \({30^0}\). Tính khoảng cách \(d\) từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\) theo \(a\).

Tam giác \(ABC\) đều cạnh $a$, \(H\) là trọng tâm tam giác nên $BH = \dfrac{2}{3}BO = \dfrac{{a\sqrt 3 }}{3}$
$ \Rightarrow HD = BD - BH = a\sqrt 3 - \dfrac{{a\sqrt 3 }}{3} = \dfrac{{2a\sqrt 3 }}{3}$
Xác định \({30^0} = \widehat {\left( {SD;\left( {ABCD} \right)} \right)} = \widehat {\left( {SD;HD} \right)} = \widehat {SDH}\) và \(SH = HD.\tan \widehat {SDH} = \dfrac{{2a\sqrt 3 }}{3}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{2a}}{3}\)
Ta có:
\(\begin{array}{l}BH \cap \left( {SCD} \right) = D \Rightarrow \dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{BD}}{{HD}} = \dfrac{3}{2}\\ \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \dfrac{3}{2}.d\left( {H;\left( {SCD} \right)} \right)\end{array}\).
Ta có \(HC \bot AB \Rightarrow HC \bot CD\).
Kẻ \(HK \bot SC\,\,\,\,\left( 1 \right)\).
Ta có \(\left\{ \begin{array}{l}CD \bot HC\\CD \bot SH\end{array} \right. \Rightarrow CD \bot \left( {SHC} \right) \Rightarrow CD \bot HK\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow HK \bot \left( {SCD} \right) \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HK\)
Tam giác vuông \(SHC\), có \(HK = \dfrac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }} = \dfrac{{\dfrac{{2a}}{3}.\dfrac{{a\sqrt 3 }}{3}}}{{\sqrt {{{\left( {\dfrac{{2a}}{3}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} }} = \dfrac{{2a\sqrt {21} }}{{21}}\).
Vậy \(d\left( {B;\left( {SCD} \right)} \right) = \dfrac{3}{2}HK = \dfrac{{a\sqrt {21} }}{7}\).
Cho hình chóp $S.ABCD$, đáy $ABCD$ là hình vuông cạnh $a$. Hình chiếu vuông góc của $S$ trên mặt phẳng $\left( {ABCD} \right)$ là điểm $H$ trùng với trung điểm của $AB$, biết $SH = a\sqrt 3 $. Gọi $M$ là giao điểm của $HD$ và $AC$. Tính khoảng cách từ điểm $M$ đến mặt phẳng $\left( {SCD} \right)$.
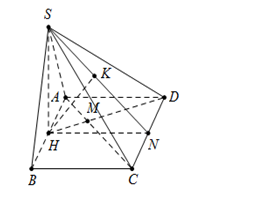
Xét $\Delta HAD$, có $AC$ là tia phân giác của góc $\widehat {HAD}$
$ \Rightarrow \dfrac{{AH}}{{AD}} = \dfrac{{HM}}{{MD}} = \dfrac{1}{2} \Rightarrow \dfrac{{HD}}{{MD}} = \dfrac{3}{2}$.
Ta có $\left\{ \begin{array}{l}H,\,M \in HD\\HM \cap \left( {SCD} \right) = D\end{array} \right. \Rightarrow \dfrac{{d\left( {H;\left( {SCD} \right)} \right)}}{{d\left( {M;\left( {SCD} \right)} \right)}} = \dfrac{{HD}}{{MD}} = \dfrac{3}{2}.$
Gọi $N$ là trung điểm của $CD \Rightarrow HN \bot CD$.
Trong $(SHN)$ từ $H$ kẻ $HK \bot SN\,\,\,\,\left( 1 \right)$, $K \in SN$
Ta có: \(\left\{ \begin{array}{l}CD \bot HN\\CD \bot SH\end{array} \right. \Rightarrow CD \bot \left( {SHN} \right) \Rightarrow CD \bot HK\,\,\,\left( 2 \right)\)
Từ (1) và (2) $ \Rightarrow HK \bot \left( {SCD} \right)$.
Khi đó $d\left( {H;\left( {SCD} \right)} \right) = HK = \dfrac{{SH.HN}}{{\sqrt {S{H^2} + H{N^2}} }} = \dfrac{{a\sqrt 3 .a}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{2}$
$ \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 3 }}{2} \Rightarrow d\left( {M;\left( {SCD} \right)} \right) = \dfrac{a}{{\sqrt 3 }}$.
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật. Cạnh bên $SA$ vuông góc với đáy, $SA = AB = a$ và $AD = x.a$. Gọi $E$ là trung điểm của $SC$. Tìm $x$, biết khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBD} \right)$ bằng $h = \dfrac{a}{3}$.
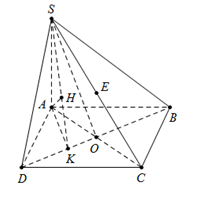
Ta có $E \in SC$, $EC \cap \left( {SBD} \right) = S \Rightarrow \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {C;\left( {SBD} \right)} \right)}} = \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \dfrac{{ES}}{{CS}} = \dfrac{1}{2}$
Từ A kẻ $ AK \bot BD\left( {K \in BD} \right)$, kẻ $AH \bot SK\,\,\left( {H \in SK} \right)\,\,\,\,\,\,\left( 1 \right)$.
Ta có: \(\left\{ \begin{array}{l}BD \bot AK\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAK} \right) \Rightarrow BD \bot AH\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AH \bot \left( {SBD} \right).\)
$ \Rightarrow AH = d\left( {A;\left( {SBD} \right)} \right) = 2.d\left( {E;\left( {SBD} \right)} \right) = \dfrac{{2a}}{3}.$
Mà $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{K^2}}} \Rightarrow AK = \dfrac{{SA.AH}}{{\sqrt {S{A^2} - A{H^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$.
Tam giác $ABD$ vuông tại $A$, có đường cao $AK$.
$ \Rightarrow \dfrac{1}{{A{B^2}}} + \dfrac{1}{{AD{}^2}} = \dfrac{1}{{A{K^2}}} \Leftrightarrow \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}{x^2}}} = \dfrac{5}{{4{a^2}}} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{x^2} = 4\end{array} \right. \Rightarrow x = 2$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $BC = a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SCA} = \widehat {BSC} = {30^0}$. Gọi $M$ là trung điểm của $CD$. Tính khoảng cách từ $D$ đến mặt phẳng $\left( {SAM} \right)$.
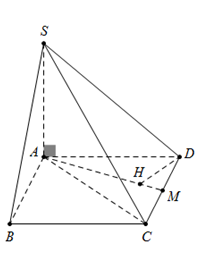
Đặt $AB = x \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{x^2} + {a^2}} \Rightarrow $$SA = AC.\tan \widehat {SCA} = \sqrt {\dfrac{{{x^2} + {a^2}}}{3}} .$
Ta có : \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB \Rightarrow \Delta SBC\) vuông tại $B,$ có $SB = \dfrac{{BC}}{{\tan \widehat {BSC}}} = a\sqrt 3 .$
Tam giác $SAB$ vuông tại $A,$ có $S{A^2} + A{B^2} = S{B^2}$.
$ \Rightarrow \dfrac{{{x^2} + {a^2}}}{3} + {x^2} = 3{a^2} \Leftrightarrow 4{x^2} = 8{a^2} \Leftrightarrow x = a\sqrt 2 .$
Kẻ $DH \bot AM$, ta có $\left\{ \begin{array}{l}SA \bot DH\\AM \bot DH\end{array} \right. \Rightarrow DH \bot \left( {SAM} \right).$
\( \Rightarrow d\left( {D;\left( {SAM} \right)} \right) = DH\)
Xét $\Delta AMD$ vuông tại $D$, có $\dfrac{1}{{D{H^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{M{D^2}}} = \dfrac{3}{{{a^2}}}.$
$ \Rightarrow DH = \dfrac{a}{{\sqrt 3 }} \Rightarrow d\left( {D;\left( {SAM} \right)} \right) = \dfrac{a}{{\sqrt 3 }}.$
Cho hình lập phương \(ABCD,{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có cạnh bằng 3a. Khoảng cách từ \({A^\prime }\) đến mặt phẳng \((ABCD)\) bằng
Ta có \(A'A \bot \left( {ABCD} \right) \Rightarrow d\left( {A',\left( {ABCD} \right)} \right) = A'A\)$=3a$.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \). Cạnh bên SA vuông góc với đáy, \(SA = 2a\).
Tính góc giữa SC và mặt phẳng \((ABCD)\).
Bước 1:
\(SA \bot \left( {ABCD} \right)\) nên AC là hình chiếu của SC lên (ABCD).
Bước 2:
Góc giữa SC và (ABCD) bằng góc giữa SC và AC và bằng \(\widehat {SCA}\)
Bước 3:
\(AC = a\sqrt 2 .\sqrt 2 = 2a\)
\(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = 1 \Rightarrow \widehat {SCA} = 45^\circ \)
Vậy góc giữa SC và (ABCD) là \(45^\circ \)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \). Cạnh bên SA vuông góc với đáy, \(SA = 2a\).
Gọi \({\rm{E}}\) là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng DE và SC.
Bước 1:
Kẻ CF||DE ( F thuộc AD).
=> DE||(SCF)
Bước 2:
=>d(DE,SC)=d(DE,(SCF))=d(D,(SCF)).
ECFD là hình bình hành nên
\(\begin{array}{l}DF = EC = \dfrac{{AD}}{2} \Rightarrow \dfrac{{AF}}{{DF}} = 3\\ \Rightarrow d\left( {D,\left( {SCF} \right)} \right) = \dfrac{1}{3}d\left( {A,\left( {SCF} \right)} \right)\end{array}\).
Bước 3:
Kẻ \(AH \bot CF;AK \bot SH\)
\(\begin{array}{l}\left. \begin{array}{l} \Rightarrow CF \bot AH\\CF \bot SA\end{array} \right\} \Rightarrow CF \bot \left( {SAH} \right)\\ \Rightarrow CF \bot AK \Rightarrow AK \bot \left( {SCF} \right)\\ \Rightarrow d\left( {A,\left( {SCF} \right)} \right) = AK\end{array}\)
Bước 4:
\(\begin{array}{l}\tan \widehat {HFA} = \tan \widehat {CFD} = \dfrac{{DC}}{{DF}} = 2\\ \Rightarrow AH = 2HF\\ \Rightarrow A{H^2} + \dfrac{{A{H^2}}}{4} = A{F^2} = {\left( {\dfrac{3}{2}.a\sqrt 2 } \right)^2}\\ \Rightarrow \dfrac{5}{4}A{H^2} = \dfrac{{9{a^2}}}{2} \Rightarrow A{H^2} = \dfrac{{18{a^2}}}{5}\\\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{S{A^2}}}\\ = \dfrac{5}{{18{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{19}}{{36{a^2}}}\\ \Rightarrow AK = \dfrac{{6a}}{{\sqrt {19} }}\\ \Rightarrow d\left( {SC,DE} \right) = \dfrac{{2a}}{{\sqrt {19} }}\end{array}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,\) \(AD = 2a\). Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Góc giữa \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^0}\). Gọi \(M\) là trung điểm \(SD\), hãy tính theo \(a\) khoảng cách \(d\) từ \(M\) đến mặt phẳng \(\left( {SAC} \right)\).
Đáp án:
Đáp án:
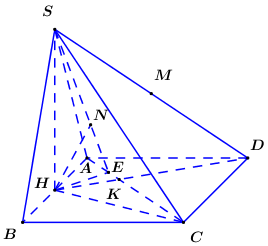
Bước 1: Đổi \(d\left( {M;\left( {SAC} \right)} \right)\) sang \(d\left( {H;\left( {SAC} \right)} \right)\).
Gọi \(H\) là trung điểm \(AB\). Vì \(\Delta SAB\) cân tại \(S\) nên \(SH \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \subset \left( {ABCD} \right),\,\,SH \bot AB\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).
Gọi \(K = HD \cap AC\). Áp dụng định lí Ta-let ta có \(\dfrac{{DK}}{{HK}} = \dfrac{{DC}}{{AH}} = 2 \Rightarrow DK = 2HK\).
Ta có \(MD \cap \left( {SAC} \right) = S \Rightarrow \dfrac{{d\left( {M;\left( {SAC} \right)} \right)}}{{d\left( {D;\left( {SAC} \right)} \right)}} = \dfrac{{SM}}{{SD}} = \dfrac{1}{2}\)
\( \Rightarrow d\left( {M;\left( {SAC} \right)} \right) = \dfrac{1}{2}d\left( {D;\left( {SAC} \right)} \right)\)
Lại có \(DH \cap \left( {SAC} \right) = K\) nên \(\dfrac{{d\left( {D;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{DK}}{{HK}} = 2 \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)\)
Bước 2: Trong \(\left( {ABCD} \right)\) kẻ \(HE \bot AC\,\,\left( {E \in AC} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HN \bot SE\,\,\left( {N \in SE} \right)\), chứng minh \(HN \bot \left( {SAC} \right)\)
Do đó \(d\left( {M;\left( {SAC} \right)} \right) = d\left( {H;\left( {SAC} \right)} \right)\)
Trong \(\left( {ABCD} \right)\) kẻ \(HE \bot AC\,\,\left( {E \in AC} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HN \bot SE\,\,\left( {N \in SE} \right)\) ta có:
\(\left\{ \begin{array}{l}AC \bot HE\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHE} \right) \)\(\Rightarrow AC \bot HN\)\(\left\{ \begin{array}{l}HN \bot SE\\HN \bot AC\end{array} \right. \Rightarrow HN \bot \left( {SAC} \right)\)\( \Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HN\)
Bước 3: Xác định góc giữa \(SC\) và \(\left( {ABCD} \right)\), từ đó tính \(SH\).
Vì \(SH \bot \left( {ABCD} \right)\) nên \(HC\) là hình chiếu vuông góc của \(SC\) lên \(\left( {ABCD} \right)\)
\( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {45^0}\)
\( \Rightarrow \Delta SHC\) vuông cân tại \(H\)\( \Rightarrow SH = HC = \sqrt {B{C^2} + B{H^2}} \)\(= \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt {17} }}{2}\)
Bước 4: Tính \(d\left( {M;\left( {SAC} \right)} \right) \)
Ta có: \({S_{HAC}} = \dfrac{1}{2}HE.AC = \dfrac{1}{2}{S_{ABC}}\)
$\Rightarrow HE.AC = \dfrac{1}{2}.AB.BC$
$ \Rightarrow HE = \dfrac{{\dfrac{1}{2}.AB.BC}}{{AC}} $$= \dfrac{{\dfrac{1}{2}.a.2a}}{{\sqrt {{a^2} + {{\left( {2a} \right)}^2}} }} $$= \dfrac{a}{{\sqrt 5 }}$
Áp dụng hệ thức lượng trong tam giác vuông \(SHE\) ta có:
Nên \(HN = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{{a\sqrt {17} }}{2}.\dfrac{a}{{\sqrt 5 }}}}{{\sqrt {\dfrac{{17{a^2}}}{4} + \dfrac{{{a^2}}}{5}} }} = \dfrac{{a\sqrt {1513} }}{{89}}\)
Vậy \(d\left( {M;\left( {SAC} \right)} \right) = \dfrac{{a\sqrt {1513} }}{{89}}\).
Cho tứ diện \(OABC\) có ba cạnh \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau. Biết khoảng cách từ điểm \(O\) đến các đường thẳng \(BC,\,\,CA,\,\,AB\) lần lượt là \(a,\,\,a\sqrt 2 ,\,\,a\sqrt 3 \). Khoảng cách từ điểm \(O\) đến mặt phẳng \(\left( {ABC} \right)\) là \(\dfrac{{2a\sqrt {m} }}{{11}}\). Tìm $m$.
Đáp án:
Đáp án:
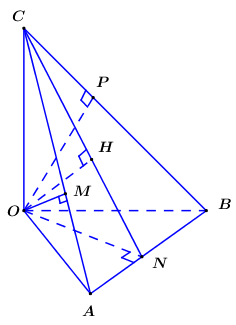
Bước 1: Kẻ \(OM \bot AC\,\,\left( {M \in AC} \right)\), \(ON \bot AB\,\,\left( {N \in AB} \right)\), \(OP \bot BC\,\,\left( {P \in BC} \right)\).
Kẻ \(OM \bot AC\,\,\left( {M \in AC} \right)\), \(ON \bot AB\,\,\left( {N \in AB} \right)\), \(OP \bot BC\,\,\left( {P \in BC} \right)\).
Khi đó ta có \(OP = a,\,\,OM = a\sqrt 2 ,\,\,ON = a\sqrt 3 \).
Bước 2: Trong \(\left( {OCN} \right)\) kẻ \(OH \bot CN\,\,\left( {H \in CN} \right)\), chứng minh \(OH \bot \left( {ABC} \right)\).
Trong \(\left( {OCN} \right)\) kẻ \(OH \bot CN\,\,\left( {H \in CN} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot ON\\AB \bot OC\end{array} \right. \Rightarrow AB \bot \left( {OCN} \right) \Rightarrow AB \bot OH\\\left\{ \begin{array}{l}OH \bot AB\\OH \bot CN\end{array} \right. \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow d\left( {O;\left( {ABC} \right)} \right) = OH\end{array}\)
Bước 3: Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Áp dụng hệ thức lượng trong tam giác vuông ta có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{N^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\)
Lại có
\(\begin{array}{l}\dfrac{1}{{O{M^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{C^2}}};\,\,\dfrac{1}{{O{N^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}};\,\,\dfrac{1}{{O{P^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\\ \Rightarrow \dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{P^2}}} = 2\left( {\dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}} \right)\\ \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{2}\left( {\dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{P^2}}}} \right)\\ \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{2}\left( {\dfrac{1}{{2{a^2}}} + \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}}} \right) = \dfrac{{11}}{{12{a^2}}}\\ \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{{11}}{{12{a^2}}} \Rightarrow OH = \dfrac{{2a\sqrt {33} }}{{11}}\end{array}\)
=> \(d\left( {O;\left( {ABC} \right)} \right) = \dfrac{{2a\sqrt {33} }}{{11}}\).
Vậy m=33.
Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình thoi cạnh $a .$ Tam giác $A B C$ đều, hình chiếu vuông góc $H$ của đỉnh $S$ trên mặt phẳng $(A B C D)$ trùng với trọng tâm của tam giác $A B C$. Đường thẳng $S D$ hợp với mặt phẳng $(A B C D)$ một góc $30^{\circ}$. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $(S C D)$ theo $a$
$d=\dfrac{ a \sqrt{21}}{7}$
$d=\dfrac{ a \sqrt{21}}{7}$
$d=\dfrac{ a \sqrt{21}}{7}$
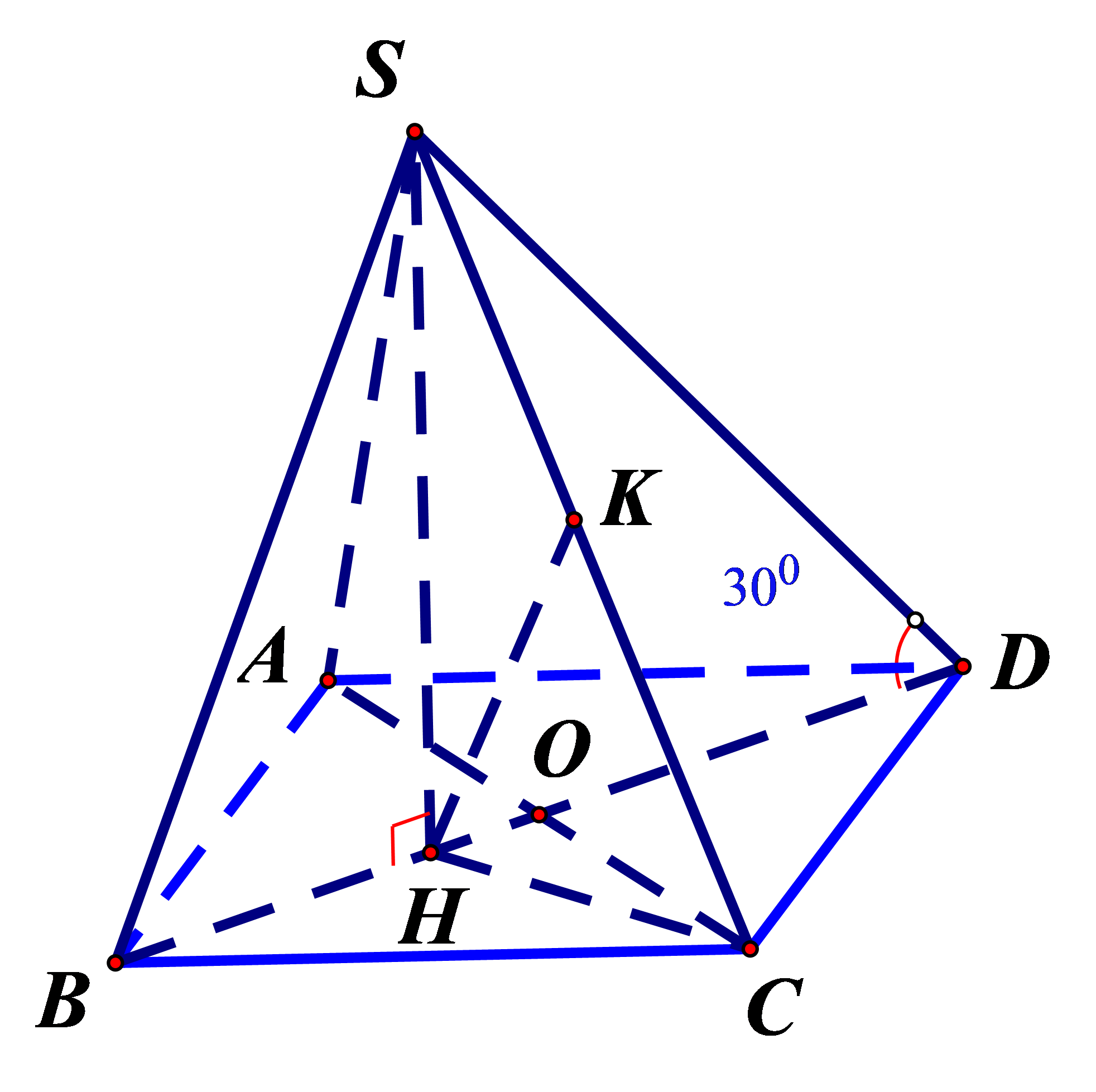
Bước 1: Gọi $O=A C \cap B D$. Tính BO, CH, HD theo a.
Gọi $O=A C \cap B D$
Ta có $\Delta A B C$ dều cạnh $a$ có $H$ là trọng tâm $\Rightarrow B O=\dfrac{a \sqrt{3}}{2}, C H=\dfrac{a \sqrt{3}}{3}, H D=\dfrac{4}{3} B O=\dfrac{2 a \sqrt{3}}{3}$
Bước 2: Tính SH theo a.
Mặt khác, $(\widehat{S D,(A B C D)})=\widehat{S D H}=30^{\circ}$
$\Rightarrow S H=H D \cdot \tan \widehat{S D H}=\dfrac{2 a}{3}$
Lại có $C H \perp A B \Rightarrow C H \perp C D$
Bước 3: Kẻ $H K \perp S C(K \in S C)$. Chứng minh \(HK \bot CD\)
Kẻ $H K \perp S C(K \in S C)$.
Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{SH \bot CD}\\{CH \bot CD}\end{array}} \right.\)\( \Rightarrow CD \bot (SHC)\)\( \Rightarrow HK \bot CD\)\( \Rightarrow HK \bot (SCD)\)
Bước 4: Tính \(d\left( {B,\left( {SCD} \right)} \right)\)
\( \Rightarrow d(H,(SCD)) = HK\)\( = \dfrac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }}\)\( = \dfrac{{2a\sqrt {21} }}{{21}}\)
Mà \(\dfrac{{d(H,(SCD))}}{{d(B,(SCD))}} = \dfrac{{HD}}{{BD}} = \dfrac{2}{3}\)\( \Rightarrow {d{(B,(SCD))}} = \dfrac{{a\sqrt {21} }}{7}\)

