Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \). Cạnh bên SA vuông góc với đáy, \(SA = 2a\).
Tính góc giữa SC và mặt phẳng \((ABCD)\).
Trả lời bởi giáo viên
Đáp án đúng: a
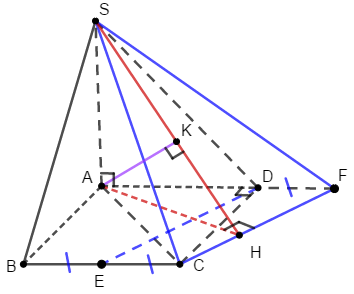
Bước 1:
\(SA \bot \left( {ABCD} \right)\) nên AC là hình chiếu của SC lên (ABCD).
Bước 2:
Góc giữa SC và (ABCD) bằng góc giữa SC và AC và bằng \(\widehat {SCA}\)
Bước 3:
\(AC = a\sqrt 2 .\sqrt 2 = 2a\)
\(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = 1 \Rightarrow \widehat {SCA} = 45^\circ \)
Vậy góc giữa SC và (ABCD) là \(45^\circ \)
Hướng dẫn giải:
Bước 1: Xác định hình chiếu của SC lên (ABCD).
Bước 2: Xác định góc giữa SC và (ABCD).
Bước 3: Tính góc giữa SC và (ABCD) theo a.

