Tổng hợp câu hay và khó chương 1

Bước 1:

$\begin{array}{l}y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\sin x + 2\sqrt 3 \cos x - m + 3} \\y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\left( {\sin x - \sqrt 3 \cos x} \right) - m + 3} \end{array}$

Bước 2:

 Đặt $t = \sin x - \sqrt 3 \cos x = 2\left( {\dfrac{1}{2}\sin x - \dfrac{{\sqrt 3 }}{2}\cos x} \right)$$= 2\sin \left( {x - \dfrac{\pi }{3}} \right)$ $\Rightarrow  - 2 \le t \le 2$.

Bước 3:

Khi đó hàm số trở thành $y = \sqrt {{t^2} - 2t - m + 3} \,\,\forall t \in \left[ { - 2;2} \right]\,\,\left( * \right)$.

Để hàm số ban đầu xác định với mọi$x \in \mathbb{R}$ thì hàm số xác định với mọi $t \in \left[ { - 2;2} \right]$.

Tức là ${t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right]$.

Bước 4:

Xét hàm số $f\left( t \right) = {t^2} - 2t - m + 3$ trên $\left[ { - 2;2} \right]$ ta có BBT:

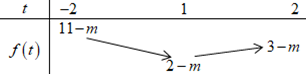
Để ${t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right]$ thì $2 - m \ge 0 \Leftrightarrow m \le 2$.

Mà $m$ nguyên dương $\Rightarrow m \in \left\{ {1;2} \right\}$.

TXĐ: $\mathbb{R}$.

Đặt $P = \sqrt {1 + \sin x}  + \sqrt {1 + \cos x}$, $P \ge 0$. Suy ra

${P^2} = 2 + \sin x + \cos x + 2\sqrt {1 + \sin x + \cos x + \sin x\cos x}$.

Đặt $t = \sin x + \cos x$$= \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right)$$\Rightarrow t \in \left[ { - \sqrt 2 \,;\,\sqrt 2 } \right]$.

Khi đó ${t^2} = 1 + 2\sin x\cos x$$\Rightarrow \sin x\cos x = \dfrac{{{t^2} - 1}}{2}$.

Do đó ${P^2} = 2 + t + 2\sqrt {1 + t + \dfrac{{{t^2} - 1}}{2}}$$= 2 + t + \sqrt 2 \left| {t + 1} \right|$.

TH1: $- \sqrt 2  \le t <  - 1$ thì:

$\begin{array}{l}t + 1 < 0 \Rightarrow \left| {t + 1} \right| =  - t - 1\\ \Rightarrow {P^2} = 2 + t + \sqrt 2 \left( { - t - 1} \right)\\ = 2 + t - \sqrt 2 t - \sqrt 2 \\ = \left( {1 - \sqrt 2 } \right)t + 2 - \sqrt 2 \end{array}$

Mà $- \sqrt 2  \le t <  - 1$ nên:

$\begin{array}{l} - \sqrt 2 \left( {1 - \sqrt 2 } \right) \ge \left( {1 - \sqrt 2 } \right)t > \left( {1 - \sqrt 2 } \right).\left( { - 1} \right)\\ \Rightarrow  - \sqrt 2  + 2 \ge \left( {1 - \sqrt 2 } \right)t >  - 1 + \sqrt 2 \\ \Rightarrow  - \sqrt 2  + 2 + 2 - \sqrt 2  \ge \left( {1 - \sqrt 2 } \right)t + 2 - \sqrt 2  >  - 1 + \sqrt 2  + 2 - \sqrt 2 \\ \Rightarrow 4 - 2\sqrt 2  \ge {P^2} > 1\\ \Rightarrow 1 < {P^2} \le 4 - 2\sqrt 2 \end{array}$

TH2: $- 1 \le t \le \sqrt 2$ thì:

$\begin{array}{l}t + 1 \ge 0 \Rightarrow \left| {t + 1} \right| = t + 1\\ \Rightarrow {P^2} = 2 + t + \sqrt 2 \left( {t + 1} \right)\\ = 2 + t + \sqrt 2 t + \sqrt 2 \\ = \left( {1 + \sqrt 2 } \right)t + 2 + \sqrt 2 \end{array}$

Mà $- 1 \le t \le \sqrt 2$ nên:

$\begin{array}{l} - 1\left( {1 + \sqrt 2 } \right) \le \left( {1 + \sqrt 2 } \right)t \le \sqrt 2 \left( {1 + \sqrt 2 } \right)\\ \Rightarrow  - 1 - \sqrt 2  \le \left( {1 + \sqrt 2 } \right)t \le \sqrt 2  + 2\\ \Rightarrow  - 1 - \sqrt 2  + 2 + \sqrt 2  \le \left( {1 + \sqrt 2 } \right)t + 2 + \sqrt 2  \le \sqrt 2  + 2 + 2 + \sqrt 2 \\ \Rightarrow 1 \le {P^2} \le 4 + 2\sqrt 2 \end{array}$

Từ 2 TH trên ta được $1 \le {P^2} \le 4 + 2\sqrt 2$.

Mà $P \ge 0$ nên $1 \le P \le \sqrt {4 + 2\sqrt 2 }$.

Phương trình có nghiệm khi $1 \le m \le \sqrt {4 + 2\sqrt 2 }$.

$2{\cos ^2}x - \sin x - 1 = 0$$\Leftrightarrow  - 2{\sin ^2}x - \sin x + 1 = 0$$\Leftrightarrow \left[ \begin{array}{l}\sin x =  - 1\\\sin x = \dfrac{1}{2}\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{2} + {k_1}2\pi \\x = \dfrac{\pi }{6} + {k_2}2\pi \\x = \dfrac{{5\pi }}{6} + {k_3}2\pi \end{array} \right.$$\left( {{k_1},{k_2},{k_3} \in \mathbb{Z}} \right)$

Do $x \in \left[ {0;20\pi } \right]$ nên:

$\left\{ \begin{array}{l}0 \le  - \dfrac{\pi }{2} + {k_1}2\pi  \le 20\pi \\0 \le \dfrac{\pi }{6} + {k_2}2\pi  \le 20\pi \\0 \le \dfrac{{5\pi }}{6} + {k_3}2\pi  \le 20\pi \end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{4} \le {k_1} \le \dfrac{{41}}{4}\\ - \dfrac{1}{{12}} \le {k_2} \le \dfrac{{119}}{{12}}\\ - \dfrac{5}{{12}} \le {k_3} \le \dfrac{{115}}{{12}}\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}{k_1} \in \left\{ {1;2;3;...;10} \right\}\\{k_2} \in \left\{ {0;1;2;...;9} \right\}\\{k_3} \in \left\{ {0;1;2;...;9} \right\}\end{array} \right.$

Vậy tổng các nghiệm của phương trình trong đoạn $\left[ {0;20\pi } \right]$ là:

$S = \sum\limits_{{k_1} = 1}^{10} {\left( { - \dfrac{\pi }{2} + {k_1}2\pi } \right) + }$$\sum\limits_{{k_2} = 0}^9 {\left( {\dfrac{\pi }{6} + {k_2}2\pi } \right)}$$+ \sum\limits_{{k_2} = 0}^9 {\left( {\dfrac{{5\pi }}{6} + {k_3}2\pi } \right)}$$= 295\pi$ .

Ta có ${\left( {\sin \dfrac{x}{2} + \cos \dfrac{x}{2}} \right)^2} + \sqrt 3 \cos x = 3$$\Leftrightarrow 1 + \sin x + \sqrt 3 \cos x = 3$$\Leftrightarrow \sin x + \sqrt 3 \cos x = 2$

$\Leftrightarrow \dfrac{1}{2}\sin x + \dfrac{{\sqrt 3 }}{2}\cos x = 1$$\Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = 1$$\Leftrightarrow x = \dfrac{\pi }{6} + k2\pi ,k \in \mathbb{Z}$.

Theo đề bài cho ta có $0 < x < 100\pi$$\Leftrightarrow 0 < \dfrac{\pi }{6} + k2\pi  < 100\pi$$\Leftrightarrow  - \dfrac{1}{{12}} < k < \dfrac{{599}}{{12}}$

Mà $k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1;2;3;4,....;48;49} \right\}$

Vậy $S = \dfrac{\pi }{6} + \dfrac{\pi }{6} + 2\pi  + \dfrac{\pi }{6} + 2 \times 2\pi  + ...... + \dfrac{\pi }{6} + 49 \times 2\pi$$= \dfrac{{50\pi }}{6} + 2\pi \left( {1 + 2 + 3 + 4 + ..... + 49} \right)$

$= \dfrac{{50\pi }}{6} + 2\pi \dfrac{{49\left( {49 + 1} \right)}}{2} = \dfrac{{7375\pi }}{3}$.

Xét $\sin x = 0 \Leftrightarrow x = m\pi$: Thay vào phương trình thấy không thỏa mãn

Xét $\sin x \ne 0 \Leftrightarrow x \ne m\pi$

$2\cos 3x\left( {2\cos 2x + 1} \right) = 1$

$\Leftrightarrow 2\left[ {\cos 5x + \cos x} \right] + 2\cos 3x = 1$

$\Leftrightarrow 2\sin x\cos 5x + 2\sin x\cos 3x + 2\sin x\cos x = \sin x$

$\Leftrightarrow \left( {\sin 6x - \sin 4x} \right) + \left( {\sin 4x - \sin 2x} \right) + \sin 2x = \sin x$

$\Leftrightarrow \sin 6x = \sin x$

$\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = \dfrac{{k2\pi }}{5}\\x = \dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}\end{array} \right.\\x \ne m\pi \end{array} \right.{\rm{  }}\left( {k,l \in \mathbb{Z}} \right)$.

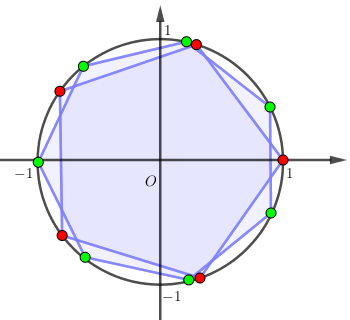
Biểu diễn các điểm của hai họ nghiệm $x = \dfrac{{k2\pi }}{5}$ và $x = \dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}$ trên đường tròn đơn vị ta thấy các điểm đều không trùng nhau. Do đó:

+) Với $\left\{ \begin{array}{l}x = \dfrac{{k2\pi }}{5}\\x \ne m\pi \\x \in \left[ { - 4\pi ;6\pi } \right]\end{array} \right.$ $\Rightarrow \left\{ \begin{array}{l}k \in \left\{ { - 10; - 9; - 8;...14;15} \right\}\\k \notin \left\{ { - 10; - 5;0;5,10,15} \right\}\end{array} \right.$

$\Rightarrow$các giá trị $x$ cần loại bỏ là $- 4\pi ,$$- 2\pi ,$$0,$$2\pi ,$$4\pi ,$$6\pi$. Tổng các giá trị này là $6\pi$

Với $\left\{ \begin{array}{l}x = \dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}\\x \ne m\pi \\x \in \left[ { - 4\pi ;6\pi } \right]\end{array} \right.$$\Rightarrow \left\{ \begin{array}{l}l \in \left\{ { - 14; - 13; - 12;...19;20} \right\}\\l \notin \left\{ { - 4; - 11;3;10;17} \right\}\end{array} \right.$

$\Rightarrow$các giá trị $x$ cần loại bỏ là $- \pi ,$$- 3\pi ,$$\pi ,$$3\pi ,$$5\pi$. Tổng các giá trị này là $5\pi$

Vậy tổng nghiệm $S = \left[ {\sum\limits_{k =  - 10}^{15} {\left( {\dfrac{{k2\pi }}{5}} \right)}  - \left( {6\pi } \right)} \right] + \left[ {\sum\limits_{l =  - 14}^{20} {\left( {\dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}} \right)}  - 5\pi } \right] = 50\pi$.

Điều kiện $\sin x\not  = 0$

$\dfrac{{\sqrt {1 + \cos x}  + \sqrt {1 - \cos x} }}{{\sin x}} = 4\cos x \Leftrightarrow \sqrt {1 + \cos x}  + \sqrt {1 - \cos x}  = 4\sin x\cos x$

$\Leftrightarrow 2 + 2\sqrt {\left( {1 + \cos x} \right)\left( {1 - \cos x} \right)}  = 16{\sin ^2}x{\cos ^2}x \Leftrightarrow 1 + \left| {\sin x} \right| = 8{\sin ^2}x\left( {1 - si{n^2}x} \right)\quad \left( 1 \right)$ (với $\sin x.\cos x \ge 0$)

TH1: $\sin x \ge 0$

$\left( 1 \right) \Leftrightarrow \left( {1 + \sin x} \right)\left( {8{{\sin }^3}x - 8{{\sin }^2}x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x =  - 1\\\sin x = \dfrac{1}{2}\\\sin x = \dfrac{{1 \pm \sqrt 5 }}{4}\end{array} \right.\mathop  \Leftrightarrow \limits^{\sin x \ge 0} \left[ \begin{array}{l}\sin x = \dfrac{1}{2}\\\sin x = \dfrac{{1 + \sqrt 5 }}{4}\end{array} \right.$

*$\sin x = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.$vì $\sin x.\cos x \ge 0$nên $x = \dfrac{\pi }{6} + k2\pi$.

*$\sin x = \dfrac{{1 + \sqrt 5 }}{4} \Leftrightarrow \left[ \begin{array}{l}x = \arcsin \left( {\dfrac{{1 + \sqrt 5 }}{4}} \right) + k2\pi \\x = \pi  - \arcsin \left( {\dfrac{{1 + \sqrt 5 }}{4}} \right) + k2\pi \end{array} \right.$ vì $\sin x.\cos x \ge 0$nên $x = \arcsin \left( {\dfrac{{1 + \sqrt 5 }}{4}} \right) + k2\pi$.

TH2: $\sin x < 0$

$\left( 1 \right) \Leftrightarrow \left( {1 - \sin x} \right)\left( { - 8{{\sin }^3}x - 8{{\sin }^2}x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\sin x =  - \dfrac{1}{2}\\\sin x = \dfrac{{ - 1 \pm \sqrt 5 }}{4}\end{array} \right.\mathop  \Leftrightarrow \limits^{\sin x < 0} \left[ \begin{array}{l}\sin x =  - \dfrac{1}{2}\\\sin x = \dfrac{{ - 1 - \sqrt 5 }}{4}\end{array} \right.$

*$\sin x =  - \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.$vì $\sin x.\cos x \ge 0$nên $x = \dfrac{{7\pi }}{6} + k2\pi$.

*$\sin x = \dfrac{{ - 1 - \sqrt 5 }}{4} \Leftrightarrow \left[ \begin{array}{l}x = \arcsin \left( {\dfrac{{ - 1 - \sqrt 5 }}{4}} \right) + k2\pi \\x = \pi  - \arcsin \left( {\dfrac{{ - 1 - \sqrt 5 }}{4}} \right) + k2\pi \end{array} \right.$

vì $\sin x.\cos x \ge 0$nên $x = \pi  - \arcsin \left( {\dfrac{{ - 1 - \sqrt 5 }}{4}} \right) + k2\pi$.

Xét nghiệm thuộc đoạn $\left[ {0;2017} \right]$:

*Với $x = \dfrac{\pi }{6} + k2\pi  \Rightarrow 0 \le \dfrac{\pi }{6} + k2\pi  \le 2017 \Leftrightarrow 0 \le k \le 320$ có $321$ nghiệm.

*Với $x = \arcsin \left( {\dfrac{{1 + \sqrt 5 }}{4}} \right) + k2\pi  = \dfrac{{3\pi }}{{10}} + k2\pi  \Rightarrow 0 \le \dfrac{{3\pi }}{{10}} + k2\pi  \le 2017 \Leftrightarrow 0 \le k \le 320$ có $321$ nghiệm.

*Với $x = \dfrac{{7\pi }}{6} + k2\pi  \Rightarrow 0 \le \dfrac{{7\pi }}{6} + k2\pi  \le 2017 \Leftrightarrow 0 \le k \le 320$ có $321$ nghiệm.

*Với $x = \pi  - \arcsin \left( {\dfrac{{ - 1 - \sqrt 5 }}{4}} \right) + k2\pi  = \dfrac{{13\pi }}{{10}} + k2\pi  \Rightarrow 0 \le \dfrac{{13\pi }}{{10}} + k2\pi  \le 2017 \Leftrightarrow 0 \le k \le 320$ có $321$ nghiệm.

*Vậy có tổng cộng $321.4 = 1284$ nghiệm thỏa yêu cầu bài toán.

Ta có: $0 \le {\sin ^2}x \le 1;$ $0 \le {\cos ^2}x \le 1$ nên $0 \le {\sin ^{2018}}x \le {\sin ^2}x;$ $0 \le {\cos ^{2018}}x \le {\cos ^2}x$

Do đó: ${\sin ^{2018}}x + {\cos ^{2018}}x \le {\sin ^2}x + {\cos ^2}x = 1$  hay $y \le 1$

Dấu $'' = ''$ xảy ra khi $\sin x = 0$ hoặc $\cos x = 0$

Lại có, áp dụng bất đẳng thức $\dfrac{{{a^n} + {b^n}}}{2} \ge {\left( {\dfrac{{a + b}}{2}} \right)^n},\left( {a,b > 0} \right)$ ta có:

${\sin ^{2018}}x + {\cos ^{2018}}x$ $= {\left( {{{\sin }^2}x} \right)^{1009}} + {\left( {{{\cos }^2}x} \right)^{1009}}$ $\ge 2.{\left( {\dfrac{{{{\sin }^2}x + {{\cos }^2}x}}{2}} \right)^{1009}} = \dfrac{1}{{{2^{1008}}}}$

Dấu $'' = ''$ xảy ra khi ${\sin ^2}x = {\cos ^2}x = \dfrac{1}{2}$

Vậy $m = \dfrac{1}{{{2^{1008}}}},M = 1$

Đặt $t = \sin x$, $t \in \left( { - 1;0} \right)$, phương trình trở thành: $2{t^2} - (2m + 1)t + 2m - 1 = 0\,\,\left( * \right)$

Yêu cầu bài toán trở thành: Tìm $m$ để phương trình $\left( * \right)$ có nghiệm $t \in \left( { - 1;0} \right)$

Có $a + b + c = 2 - \left( {2m + 1} \right) + 2m - 1 = 0$  nên $\left( * \right)$ luôn có hai nghiệm ${t_1} = \dfrac{{2m - 1}}{2},{t_2} = 1$

Bài toán thỏa $\Leftrightarrow  - 1 < \dfrac{{2m - 1}}{2} < 0$ $\Leftrightarrow  - \dfrac{1}{2} < m < \dfrac{1}{2}$

Ta có: ${\cos ^2}x + \sqrt {\cos x + m}  = m$ suy ra $m \ge 0$.

Đặt $\sqrt {\cos x + m}  = t$, $t \ge 0$. Phương trình trở thành: $\left\{ \begin{array}{l}{\cos ^2}x + t = m\\{t^2} - \cos x = m\end{array} \right.$

$\Rightarrow \,\left( {{{\cos }^2}x - {t^2}} \right) + \left( {t + \cos x} \right) = 0$$\Leftrightarrow \left( {\cos x + t} \right)\left( {\cos x - t + 1} \right) = 0$$\Leftrightarrow \left[ \begin{array}{l}\cos x =  - t\\\cos x - t + 1 = 0\end{array} \right.$

+) Trường hợp $1$: $\cos x =  - t$ $\Rightarrow \sqrt {\cos x + m}  =  - \cos x$ $\Leftrightarrow \left\{ \begin{array}{l}\cos x \le 0\\{\cos ^2}x - \cos x = m\end{array} \right.$

Đặt $u = \cos x$$\left( { - 1 \le u \le 0} \right)$

Xét hàm số $f\left( u \right) = {u^2} - u$ trên đoạn $\left[ { - 1;0} \right]$, có hoành độ đỉnh $x = \dfrac{1}{2} \notin \left[ { - 1;0} \right]$ và bảng biến thiên:

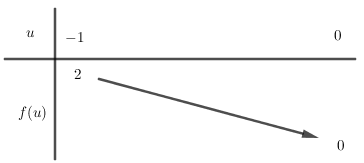
Để phương trình có nghiệm thì $m \in \left[ {0;\,2} \right]$.

Vì $m \in \mathbb{Z}$ nên $m \in \left\{ {0;\,1;\,2} \right\}$.

+) Trường hợp $2$: $\cos x - t + 1 = 0$$\Leftrightarrow \sqrt {\cos x + m}  = 1 + \cos x$$\Leftrightarrow {\cos ^2}x + \,\cos x + 1 = m$.

Đặt $v = \cos x$, $- 1 \le v \le 1$. Ta có $m = {v^2} + v + 1 = g\left( v \right)$

Hàm số bậc hai $g\left( v \right)$ có hoành độ đỉnh $v =  - \dfrac{1}{2} \in \left[ { - 1;1} \right]$ có bảng biến thiên :

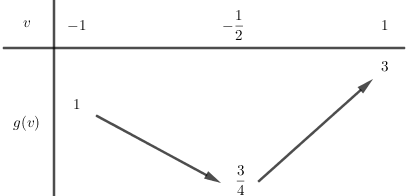
Để phương trình có nghiệm thì $m \in \left[ {\dfrac{3}{4};3} \right]$.

Vì $m \in \mathbb{Z}$ nên $m \in \left\{ {1;\,2;\,3} \right\}$.

Vậy có tất cả $4$ số nguyên $m$ thỏa mãn bài toán.

Ta có: ${\sin ^{2015}}x - {\cos ^{2016}}x = 2\left( {{{\sin }^{2017}}x - {{\cos }^{2018}}x} \right) + \cos 2x$

$\Leftrightarrow {\sin ^{2015}}x\left( {1 - 2{{\sin }^2}x} \right) + {\cos ^{2016}}x\left( {2{{\cos }^2}x - 1} \right) = \cos 2x$

$\Leftrightarrow {\sin ^{2015}}x.\cos 2x + {\cos ^{2016}}x.\cos 2x = \cos 2x$$\Leftrightarrow \left[ \begin{array}{l}\cos 2x = 0\\{\sin ^{2015}}x + {\cos ^{2016}}x = 1\end{array} \right.$.

Với $\cos 2x = 0$$\Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}$

Vì $x \in \left[ { - 10;30} \right]$$\Rightarrow  - 10 \le \dfrac{\pi }{4} + k\dfrac{\pi }{2} \le 30$$\Leftrightarrow  - \dfrac{{20}}{\pi } - \dfrac{1}{2} \le k \le \dfrac{{60}}{\pi } - \dfrac{1}{2}$$\Rightarrow  - 6 \le k \le 18$.

Với ${\sin ^{2015}}x + {\cos ^{2016}}x = 1$. Ta có ${\sin ^{2015}}x \le {\sin ^2}x;{\cos ^{2016}}x \le {\cos ^2}x$.

Do đó $1 = {\sin ^{2015}}x + {\cos ^{2016}}x \le {\sin ^2}x + {\cos ^2}x = 1$ suy ra $\left[ \begin{array}{l}\sin x = 0,\cos x =  \pm 1\\\sin x = 1,\cos x = 0\end{array} \right.$.

Nếu $\sin x = 0 \Leftrightarrow x = k\pi ,k \in \mathbb{Z}$.

Vì $x \in \left[ { - 10;30} \right]$$\Rightarrow  - 10 \le k\pi  \le 30$$\Leftrightarrow \dfrac{{ - 10}}{\pi } \le k  \le \dfrac{{30}}{\pi }$ $\Rightarrow  - 3 \le k \le 9$.

Nếu $\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}$.

Vì $x \in \left[ { - 10;30} \right]$$\Rightarrow  - 10 \le \dfrac{\pi }{2} + k2\pi  \le 30$$\Leftrightarrow  - \dfrac{5}{\pi } - \dfrac{1}{4} \le k \le \dfrac{{15}}{\pi } - \dfrac{1}{4}$$\Rightarrow  - 1 \le k \le 4$.

Ngoài ra điểm diểu diễn các nghiệm của mỗi họ nghiệm $x=\dfrac{\pi }{4} + k\dfrac{\pi }{2}; x = k\pi ; x = \dfrac{\pi }{2} + k2\pi$ đều phân biệt nên các nghiệm thỏa bài toán là khác nhau.

Vậy số nghiệm của phương trình đã cho là: $13 + 6 + 25 = 44$.

Ta có $x \in \left( {0\,;\,\dfrac{{3\pi }}{4}} \right)$$\Rightarrow \dfrac{\pi }{4} < x + \dfrac{\pi }{4} < \pi$$\Rightarrow 0 < \sin \left( {x + \dfrac{\pi }{4}} \right) \le 1$$\Rightarrow 0 < \sqrt[{}]{2}\sin \left( {x + \dfrac{\pi }{4}} \right) \le \sqrt[{}]{2}$.

Mặt khác $\sqrt[{}]{2}\sin \left( {x + \dfrac{\pi }{4}} \right) = \sin x + \cos x$.

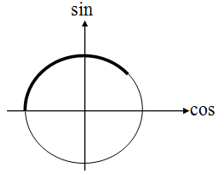
Đặt $\sin x + \cos x = t$ với $t \in \left( {0\,;\,\sqrt[{}]{2}} \right]$$\Rightarrow {\sin ^2}x + {\cos ^2}x + 2\sin x.\cos x = {t^2}$ $\Rightarrow \sin 2x = {t^2} - 1$.

Nhận thấy với mỗi giá trị của $t$ trong $\left( {0;1} \right]$ hoặc $t = \sqrt 2$ thì đều có một giá trị của $x \in \left( {0;\dfrac{{3\pi }}{4}} \right)$, nếu $t \in \left[ {1;\sqrt 2 } \right)$ thì sẽ có $2$ giá trị của $x \in \left( {0;\dfrac{{3\pi }}{4}} \right)$

Phương trình đã cho trở thành ${t^2} - 1 + t - 2 = m \Leftrightarrow {t^2} + t - 3 = m$$\left( * \right)$.

Xét $f\left( t \right) = {t^2} + t - 3$ với $t \in \left( {0\,;\,\sqrt[{}]{2}} \right]$ có đồ thị là parabol, hoành độ đỉnh $t =  - \dfrac{1}{2} \notin \left( {0;\sqrt 2 } \right]$

Bảng biến thiên:

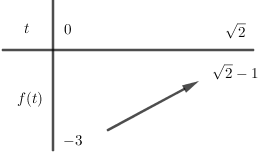
Dựa vào bảng biến thiên ta có phương trình $\left( * \right)$ có nhiều nhất một nghiệm $t$.

Do đó để phương trình đã cho có đúng một nghiệm thực $x$ thuộc khoảng $\left( {0\,;\,\dfrac{{3\pi }}{4}} \right)$ thì $\left[ \begin{array}{l}t = \sqrt[{}]{2}\\0 < t \le 1\end{array} \right.$.

Với $t = \sqrt[{}]{2}$ thay vào phương trình $\left( * \right)$: $2 + \sqrt[{}]{2} - 3 = m$$\Leftrightarrow m = \sqrt[{}]{2} - 1 \notin \mathbb{Z}$.

Với $0 < t \le 1$ ta có bảng biến thiên

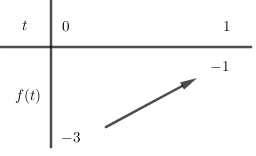
Vậy $- 3 < m \le  - 1$$\Rightarrow$ có $2$ giá trị nguyên của $m$ là $- 2$ và $- 1$.

Ta có: $\left( {1 + \cos x} \right)\left( {\cos 4x - m\cos x} \right) = m{\sin ^2}x \Leftrightarrow \left( {1 + \cos x} \right)\left( {\cos 4x - m\cos x} \right) - m\left( {1 - {{\cos }^2}x} \right) = 0$

$\Leftrightarrow \left( {1 + \cos x} \right)\left[ {\cos 4x - m\cos x - m\left( {1 - \cos x} \right)} \right] = 0$$\Leftrightarrow \left[ \begin{array}{l}\cos x =  - 1\\\cos 4x = m\end{array} \right.$.

Xét phương trình $\cos x =  - 1 \Leftrightarrow x = \pi  + k2\pi$ $\left( {k \in \mathbb{Z}} \right)$.

Phương trình $\cos x =  - 1$ không có nghiệm trong đoạn $\left[ {0\,;\,\dfrac{{2\pi }}{3}} \right]$.

Xét $\cos 4x = m$. Ta có $x \in \left[ {0\,;\,\dfrac{{2\pi }}{3}} \right] \Leftrightarrow 4x \in \left[ {0;\,\dfrac{{8\pi }}{3}} \right]$.

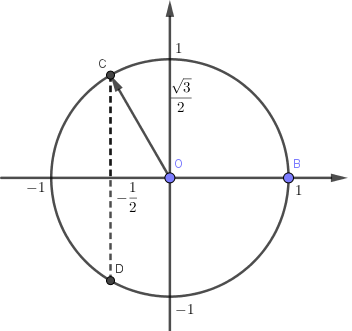
Quan sát hình vẽ ta thấy,

Với $4x \in \left[ {0\,;\,2\pi } \right]\backslash \left\{ \pi  \right\}$ và $m \in \left( { - 1\,;\,1} \right]$ phương trình $\cos 4x = m$ có $2$ nghiệm.

Với $4x \in \left( {2\pi \,;\,\dfrac{{8\pi }}{3}} \right]$ và $m \in \left[ { - \dfrac{1}{2}\,;\,1} \right)$ phương trình $\cos 4x = m$ có $1$ nghiệm.

Vậy phương trình có $3$ nghiệm phân biệt thuộc $\left[ {0\,;\,\dfrac{{2\pi }}{3}} \right]$ khi $m \in \left[ { - \dfrac{1}{2}\,;\,1} \right)$.

Phương trình đã cho tương đương với $\sin \left( {\dfrac{x}{{{x^2} + 6}}} \right) = \sin \left( {\dfrac{{80}}{{{x^2} + 32x + 332}}} \right)\quad \left(  *  \right)$.

Ta biết rằng hàm số $y = \sin x$ đồng biến trên khoảng $\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)$. Ta chỉ ra rằng các hàm số $f\left( x \right) = \dfrac{x}{{{x^2} + 6}}$ và $g\left( x \right) = \dfrac{{80}}{{{x^2} + 32x + 332}}$ nhận giá trị trong khoảng này.

Thật vậy, ta có $\left| {\dfrac{x}{{{x^2} + 6}}} \right| \le \left| {\dfrac{x}{{2\sqrt {6{x^2}} }}} \right| = \dfrac{1}{{2\sqrt 6 }}$

và $0 < \dfrac{{80}}{{{x^2} + 32x + 332}} = \dfrac{{80}}{{{{\left( {x + 16} \right)}^2} + 76}} \le \dfrac{{80}}{{76}} < \dfrac{\pi }{2}$

Từ các đánh giá trên, $\left(  *  \right)$ xảy ra khi và chỉ khi

$\dfrac{x}{{{x^2} + 6}} = \dfrac{{80}}{{{x^2} + 32x + 332}}$ $\Leftrightarrow {x^3} - 48{x^2} + 332x - 480 = 0$ $\Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 6\\x = 40\end{array} \right.$.

Tổng các nghiệm của phương trình đã cho là $2 + 6 + 40 = 48$.

Ta có: $- 1 \le \sin x \le 1; - 1 \le \cos x \le 1$

$\begin{array}{l}{\sin ^3}x + {\sin ^2}x = {\sin ^2}x\left( {\sin x + 1} \right) \ge 0\\{\sin ^3}x - {\sin ^2}x = {\sin ^2}x\left( {\sin x - 1} \right) \le 0\end{array}$

Do đó $- {\sin ^2}x \le {\sin ^3}x \le {\sin ^2}x$

Tương tự $- {\cos ^2}x \le {\cos ^3}x \le {\cos ^2}x$

$\Rightarrow  - 2{\sin ^2}x - {\cos ^2}x \le y \le 2{\sin ^2}x + {\cos ^2}x$

Mà $\left\{ \begin{array}{l} - 2{\sin ^2}x - {\cos ^2}x =  - 1 - {\sin ^2}x \ge  - 1 - 1 =  - 2\\2{\sin ^2}x + {\cos ^2}x = 1 + {\sin ^2}x \le 1 + 1 = 2\end{array} \right.$  nên $- 2 \le y \le 2$

Vậy $M = 2$ đạt được khi $\sin x = 1,\cos x = 0$

 $m =  - 2$ đạt được khi $\sin x =  - 1,\cos x = 0$

Do đó ${M^2} + {m^2} = 8$