Cho phương trình \(\left( {1 + \cos x} \right)\left( {\cos 4x - m\cos x} \right) = m{\sin ^2}x\). Tìm tất cả các giá trị của \(m\) để phương trình có đúng \(3\) nghiệm phân biệt thuộc \(\left[ {0\,;\,\dfrac{{2\pi }}{3}} \right]\).

Ta có: \(\left( {1 + \cos x} \right)\left( {\cos 4x - m\cos x} \right) = m{\sin ^2}x \Leftrightarrow \left( {1 + \cos x} \right)\left( {\cos 4x - m\cos x} \right) - m\left( {1 - {{\cos }^2}x} \right) = 0\)

\( \Leftrightarrow \left( {1 + \cos x} \right)\left[ {\cos 4x - m\cos x - m\left( {1 - \cos x} \right)} \right] = 0\)\( \Leftrightarrow \left[ \begin{array}{l}\cos x =  - 1\\\cos 4x = m\end{array} \right.\).

Xét phương trình \(\cos x =  - 1 \Leftrightarrow x = \pi  + k2\pi \) \(\left( {k \in \mathbb{Z}} \right)\).

Phương trình \(\cos x =  - 1\) không có nghiệm trong đoạn \(\left[ {0\,;\,\dfrac{{2\pi }}{3}} \right]\).

Xét $\cos 4x = m$. Ta có \(x \in \left[ {0\,;\,\dfrac{{2\pi }}{3}} \right] \Leftrightarrow 4x \in \left[ {0;\,\dfrac{{8\pi }}{3}} \right]\).

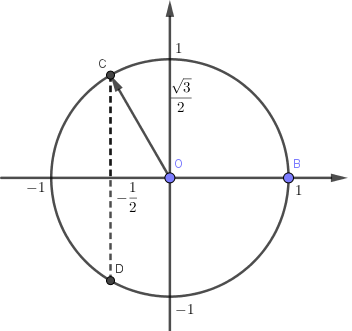
Quan sát hình vẽ ta thấy,

Với \(4x \in \left[ {0\,;\,2\pi } \right]\backslash \left\{ \pi  \right\}\) và $m \in \left( { - 1\,;\,1} \right]$ phương trình $\cos 4x = m$ có $2$ nghiệm.

Với \(4x \in \left( {2\pi \,;\,\dfrac{{8\pi }}{3}} \right]\) và $m \in \left[ { - \dfrac{1}{2}\,;\,1} \right)$ phương trình $\cos 4x = m$ có $1$ nghiệm.

Vậy phương trình có $3$ nghiệm phân biệt thuộc \(\left[ {0\,;\,\dfrac{{2\pi }}{3}} \right]\) khi $m \in \left[ { - \dfrac{1}{2}\,;\,1} \right)$.