Một số phương trình lượng giác thường gặp

Bước 1: Đặt $t = \sin x + \cos x,(|t| \le \sqrt 2 )$. Đánh giá ${(t - 1)^2}$

Phương trình $\sin x\cos x - \sin x - \cos x$$+ m = 0(1)$ có nghĩa $\forall x \in \mathbb{R}$.

Đặt $t = \sin x + \cos x,(|t| \le \sqrt 2 )$. Ta có: $\sin x\cos x = \dfrac{{{t^2} - 1}}{2}$

$\Rightarrow (1) \Leftrightarrow \dfrac{{{t^2} - 1}}{2} - t + m = 0$$\Leftrightarrow  - 2m = {t^2} - 2t - 1$$\Leftrightarrow {(t - 1)^2} =  - 2m + 2$

Do $- \sqrt 2  \le t \le \sqrt 2$$\Rightarrow  - \sqrt 2  - 1 \le t - 1 \le \sqrt 2  - 1$$\Rightarrow 0 \le {(t - 1)^2} \le 3 + 2\sqrt 2 .$

Bước 2: Đánh giá m và tìm số giá trị nguyên của m.

Để phương trình có nghiệm thì $0 \le  - 2m + 2 \le 3 + 2\sqrt 2$$\Leftrightarrow  - \dfrac{{1 + 2\sqrt 2 }}{2} \le m \le 1$.

Vì $m \in \mathbb{Z}$ nên $m \in \{  - 1;0;1\}$.

Vậy có 3 giá trị nguyên của m cần tìm.

Bước 1:

Ta có $\sin x + \sqrt 3 \cos x = 2 \Leftrightarrow \dfrac{1}{2}sinx + \dfrac{{\sqrt 3 }}{2}\cos x = 1$

Bước 2:

$\Leftrightarrow \sin \dfrac{\pi }{6}.\sin x + \cos \dfrac{\pi }{6}.\cos x = 1 \Leftrightarrow c{\rm{os}}\left( {x - \dfrac{\pi }{6}} \right) = 1$

Bước 3:

$\Leftrightarrow x - \dfrac{\pi }{6} = k2\pi  \Leftrightarrow x = \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right).$

Bước 1:

$\begin{array}{l}3{\cos ^2}x + 2\cos x - 5 = 0\\ \Leftrightarrow \left( {3\cos x + 5} \right)\left( {\cos x - 1} \right) = 0\end{array}$

Bước 2:

$\Leftrightarrow \left[ \begin{array}{l}\cos x = 1\\\cos x =  - \dfrac{5}{3}\left( {loai} \right)\end{array} \right. \Leftrightarrow \cos x = 1$

Bước 3:

$\Leftrightarrow x = k2\pi \left( {k \in \mathbb{Z}} \right).$

Bước 1: Đưa phương trình về dạng $f\left( {\cos 2x} \right) = g\left( m \right)$

Ta có: $4\left( {{{\sin }^4}x + {{\cos }^4}x} \right) + {\sin ^2}2x + 4m$$= 4\cos 2x$

$\Leftrightarrow 4\left[ {{{\left( {{{\sin }^2}x + {{\cos }^2}x} \right)}^2} - 2{{\sin }^2}x{{\cos }^2}x} \right]$$+ {\sin ^2}2x - 4\cos 2x + 4m = 0$

$\Leftrightarrow 4 - {\sin ^2}2x - 4\cos 2x + 4m = 0$$\Leftrightarrow {\cos ^2}2x - 4\cos 2x =  - 4m - 3$

Bước 2: Đặt $t = \cos 2x(t \in [ - 1;1])$. Đưa vế phải hàm đa thức biến t và khảo sát hàm số.

Đặt $t = \cos 2x(t \in [ - 1;1])$. Ta có phương trình ${t^2} - 4t =  - 4m - 3(*)$ với $t \in [ - 1;1]$.

Phương trình đã cho có nghiệm $x$ khi và chỉ khi phương trình $(*)$ có nghiệm $t \in [ - 1;1]$.

Lập bảng biến thiên của hàm $f(t) = {t^2} - 4t$ trên $[ - 1;1]$.

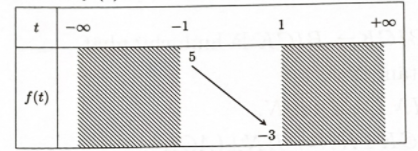
Từ bảng biến thiên ta thấy phương trình có nghiệm $t \in [ - 1;1]$ khi và chỉ khi $- 3 \le  - 4m - 3 \le 5 \Leftrightarrow  - 2 \le m \le 0$. Vậy $a =  - 2;b = 0$ suy ra $2b - a = 2$.

Bước 1:

Ta có $3{\tan ^2}x + \left( {6 - \sqrt 3 } \right)\tan x - 2\sqrt 3  = 0\left( 1 \right)$

Đặt  $\tan x = t$

Bước 2:

Phương trình (1) trở thành: $3{t^2} + \left( {6 - \sqrt 3 } \right)t - 2\sqrt 3  = 0$

$\Leftrightarrow \left[ \begin{array}{l}t = \dfrac{{\sqrt 3 }}{3}\\t =  - 2\end{array} \right.$

Bước 3:

$\Leftrightarrow \left[ \begin{array}{l}\tan x = \dfrac{{\sqrt 3 }}{3}\\\tan x =  - 2\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = \arctan \left( { - 2} \right) + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Bước 1:

Ta có $- \sqrt {2 - m} \sin x + \left( {m + 1} \right)\cos x = m - 1$(*)

TXĐ: $m \le 2.$

Bước 2:

Phương trình (*) có $a= - \sqrt {2 - m}$, $b=\left( {m + 1} \right)$ và $c=m - 1$

Khi đó phương trình (*) có nghiệm khi $a^2+b^2\ge c^2$

$\Leftrightarrow {\left( { - \sqrt {2 - m}} \right)^2}+{\left( {m + 1} \right)^2}  \ge {\left( {m - 1} \right)^2}$

$\begin{array}{l} \Leftrightarrow 2 - m + \left( {{m^2} + 2m + 1} \right) \ge {m^2} - 2m + 1\\ \Leftrightarrow 3m + 2 \ge 0\end{array}$

$\Leftrightarrow m \ge -\dfrac{2}{3}$

Bước 3:

Kết hợp điều kiện ta có $-\dfrac{2}{3} \le m \le 2$.

$\left( {2\sin x - 1} \right)\left( {\sqrt 3 \tan x + 2\sin x} \right) = 3 - 4{\cos ^2}x\,\,\left( * \right)$

Điều kiện: $\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi$.

$\begin{array}{l}\left( * \right) \Leftrightarrow \left( {2\sin x - 1} \right).\dfrac{{\sqrt 3 \sin x + 2\sin x\cos x}}{{\cos x}} = 3 - 4{\cos ^2}x\\ \Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sqrt 3 \sin x + \sin 2x} \right) + \left( {4{{\cos }^3}x - 3\cos x} \right) = 0\\ \Leftrightarrow 2\sqrt 3 {\sin ^2}x - \sqrt 3 \sin x + 2\sin x\sin 2x - \sin 2x + \cos 3x = 0\\ \Leftrightarrow 2\sqrt 3 {\sin ^2}x - \sqrt 3 \sin x + \cos x - \cos 3x - \sin 2x + \cos 3x = 0\\ \Leftrightarrow \sqrt 3 \sin x\left( {2\sin x - 1} \right) - \sin 2x + \cos x = 0\\ \Leftrightarrow \sqrt 3 \sin x\left( {2\sin x - 1} \right) - \cos x\left( {2\sin x - 1} \right) = 0\\ \Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sqrt 3 \sin x - \cos x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2\sin x - 1 = 0\,\,\left( 1 \right)\\\sqrt 3 \sin x - \cos x = 0\,\,\left( 2 \right)\end{array} \right.\end{array}$

Giải $\left( 1 \right) \Leftrightarrow \sin x = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.$.

Giải $\left( 2 \right) \Leftrightarrow \sqrt 3 \sin x = \cos x \Leftrightarrow \sqrt 3 \tan x = 1 \Leftrightarrow \tan x = \dfrac{1}{{\sqrt 3 }} \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \left( {TM} \right)$.

Hợp nghiệm của $\left( 1 \right)$ và $\left( 2 \right)$ ta được $\left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$.

Mà $x \in \left[ {0;20\pi } \right] \Rightarrow x \in \left\{ {\dfrac{\pi }{6};\dfrac{\pi }{6} + \pi ;...;\dfrac{\pi }{6} + 19\pi ;\dfrac{{5\pi }}{6};\dfrac{{5\pi }}{6} + 2\pi ;...\dfrac{{5\pi }}{6} + 18\pi } \right\}$

Vậy tổng các nghiệm là:

$\begin{array}{l}\,\,\,\,\,\dfrac{\pi }{6} + \dfrac{\pi }{6} + \pi  + \dfrac{\pi }{6} + 2\pi  + ... + \dfrac{\pi }{6} + 19\pi  + \dfrac{{5\pi }}{6} + \dfrac{{5\pi }}{6} + 2\pi  + ... + \dfrac{{5\pi }}{6} + 18\pi \\ = 20.\dfrac{\pi }{6} + \left( {1 + 2 + 3 + ... + 19} \right)\pi  + \dfrac{{5\pi }}{6}.10 + 2\pi \left( {1 + 2 + ... + 9} \right) = \dfrac{{875\pi }}{3}\end{array}$.

Ta có : ${\sin ^2}x + \sqrt 3 \sin x\cos x = 1$$\Leftrightarrow \dfrac{{1 - \cos 2x}}{2} + \dfrac{{\sqrt 3 }}{2}\sin 2x = 1$

$\begin{array}{l} \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\sin 2x - \dfrac{1}{2}\cos 2x = \dfrac{1}{2} \\\Leftrightarrow \dfrac{1}{2}\cos 2x - \dfrac{{\sqrt 3 }}{2}\sin 2x = \dfrac{1}{2}\\ \Leftrightarrow \cos \dfrac{\pi }{3}.\cos 2x - \sin \dfrac{\pi }{3}\sin 2x = \dfrac{1}{2}\\ \Leftrightarrow \cos \left( {2x + \dfrac{\pi }{3}} \right) = \cos \dfrac{\pi }{3} \\\Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{3} = \dfrac{\pi }{3} + k2\pi \\2x + \dfrac{\pi }{3} =  - \dfrac{\pi }{3} + m2\pi \end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x =  - \dfrac{\pi }{3} + m\pi \end{array} \right.\left( {k,\,m \in \mathbb{Z}} \right)\end{array}$

Vì $x \in \left[ {0;2\pi } \right]$ nên ta có

+ $0 \le k\pi  \le 2\pi  \Leftrightarrow 0 \le k \le 2$$\Leftrightarrow \left[ \begin{array}{l}k = 0 \Rightarrow x = 0\\k = 1 \Rightarrow x = \pi \\k = 2 \Rightarrow x = 2\pi \end{array} \right.$ 

+ $0 \le  - \dfrac{\pi }{3} + m2\pi  \le 2\pi$$\Leftrightarrow \dfrac{1}{6} \le m \le \dfrac{7}{6} \Leftrightarrow m = 1 \Rightarrow x = \dfrac{{2\pi }}{3}.$

Vậy có bốn nghiệm thuộc $\left[ {0;2\pi } \right]$

Bước 1:

Ta có : $\sin x + \cos x = 1 - \dfrac{1}{2}\sin 2x$$\Leftrightarrow \sin x + \cos x = 1 - \sin x\cos x$

Bước 2:

Đặt $\sin x + \cos x = t\,\,\,\left( { - \sqrt 2  \le t \le \sqrt 2 } \right)$

$\Rightarrow (\sin x + \cos x )^2=t^2$ $\Leftrightarrow \sin^2 x + \cos^2 x +2\sin x.\cos x=t^2$

$\Leftrightarrow 1 +2\sin x.\cos x=t^2$$\Rightarrow \sin x\cos x = \dfrac{{{t^2} - 1}}{2}$

Khi đó phương trình trở thành:

$t = 1 - \dfrac{{{t^2} - 1}}{2} = 0 \Leftrightarrow 2t + {t^2} - 1 - 2 = 0$ $\Leftrightarrow {t^2} + 2t - 3 = 0$

$\Leftrightarrow \left[ \begin{array}{l}t = 1\left( {tm} \right)\\t =  - 3\left( {ktm} \right)\end{array} \right. \Leftrightarrow t = 1$

Bước 3:

Suy ra $\sin x + \cos x = 1$

$\begin{array}{l} \Leftrightarrow \left( {\dfrac{1}{{\sqrt 2 }}\sin x + \dfrac{1}{{\sqrt 2 }}\cos x} \right) = \dfrac{1}{\sqrt 2}\\ \Leftrightarrow  \cos \left( { \dfrac{\pi }{4}} \right).\sin x+ \sin \left( { \dfrac{\pi }{4}} \right).\cos x= \dfrac{1}{\sqrt 2}\\ \Leftrightarrow  \sin \left( {x + \dfrac{\pi }{4}} \right) = \dfrac{1}{\sqrt 2}\end{array}$

Bước 4:

$\Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = \sin \dfrac{\pi }{4}$

$\Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{4} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{4} = \dfrac{{3\pi }}{4} + k2\pi \end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)$

Bước 5:

Do $x$ là nghiệm âm lớn nhất nên:

+ TH1: $k2\pi  < 0 \Leftrightarrow k < 0\mathop  \Rightarrow \limits^{k \in \mathbb{Z}} k =  - 1 \Rightarrow x =  - 2\pi$

+ TH2: $\dfrac{\pi }{2} + k2\pi  < 0 \Leftrightarrow k <  - \dfrac{1}{4}\mathop  \Rightarrow \limits^{k \in \mathbb{Z}} k =  - 1$$\Rightarrow x =  - \dfrac{{3\pi }}{2}$.

Trong hai nghiệm $- 2\pi$ và $- \dfrac{{3\pi }}{2}$ thì nghiệm âm lớn nhất là $- \dfrac{{3\pi }}{2}$.

Bước 1: Giải phương trình. Sử dụng công thức ${\cos ^2}x = 1 - {\sin ^2}x$

Phương trình $- 2{\cos ^2}x - 5\sin x + 4 = 0$

$\Leftrightarrow  - 2\left( {1 - {{\sin }^2}x} \right) - 5\sin x + 4 = 0$

$\Leftrightarrow 2{\sin ^2}x - 5\sin x + 2 = 0$$\Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin x = 2}\\{\sin x = \dfrac{1}{2}}\end{array}} \right.$

$\Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \dfrac{\pi }{6} + k2\pi }\\{x = \dfrac{{5\pi }}{6} + l2\pi }\end{array}(k,l \in \mathbb{Z})} \right.$

$\left[ {\begin{array}{*{20}{l}}{\sin x = 2}\\{\sin x = \dfrac{1}{2}}\end{array} \Rightarrow \sin x = \dfrac{1}{2} = \sin \dfrac{\pi }{6}} \right.$

Bước 2: Tìm nghiệm $x \in \left[ {0;\dfrac{{9\pi }}{2}} \right]$

Vì $x \in \left[ {0;\dfrac{{9\pi }}{2}} \right]$ nên $\left[ {\begin{array}{*{20}{l}}{0 \le \dfrac{\pi }{6} + k2\pi  \le \dfrac{{9\pi }}{2}}\\{0 \le \dfrac{{5\pi }}{6} + l2\pi  \le \dfrac{{9\pi }}{2}}\end{array}} \right.$$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - \dfrac{1}{6} \le 2k \le \dfrac{9}{2} - \dfrac{1}{6}}\\{ - \dfrac{5}{6} \le 2l \le \dfrac{9}{2} - \dfrac{5}{6}}\end{array}} \right.$$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - \dfrac{1}{{12}} \le k \le \dfrac{{13}}{6}}\\{ - \dfrac{5}{{12}} \le l \le \dfrac{{11}}{6}}\end{array}} \right.$

$\Rightarrow \left[ {\begin{array}{*{20}{l}}{k \in \{ 0,1,2\} }\\{l \in \{ 0,1\} }\end{array}} \right.$.

=> Có 5 giá trị thỏa mãn.

Vậy phương trình có 5 nghiệm.

$\begin{array}{l}\,\,\,\,\,4\cos x\sin \left( {\dfrac{\pi }{6} + x} \right)\sin \left( {\dfrac{\pi }{6} - x} \right) = \cos 2x\\ \Leftrightarrow 4\cos x.\left( { - \dfrac{1}{2}\left( {\cos \dfrac{\pi }{3} - \cos 2x} \right)} \right) = \cos 2x\\ \Leftrightarrow  - 2\cos x\left( {\dfrac{1}{2} - \cos 2x} \right) = \cos 2x\\ \Leftrightarrow  - \cos x + 2\cos x\cos 2x = \cos 2x\\ \Leftrightarrow  - \cos x + 2\cos x\left( {2{{\cos }^2}x - 1} \right) = 2{\cos ^2}x - 1\\ \Leftrightarrow  - \cos x + 4{\cos ^3}x - 2\cos x = 2{\cos ^2}x - 1\\ \Leftrightarrow 4{\cos ^3}x - 2{\cos ^2}x - 3\cos x + 1 = 0\\ \Leftrightarrow \left( {\cos x - 1} \right)\left( {4{{\cos }^2}x + 2\cos x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = 1\\\cos x = \dfrac{{ - 1 \pm \sqrt 5 }}{4}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x =  \pm \arccos \dfrac{{ - 1 \pm \sqrt 5 }}{4} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy nghiệm của phương trình đã cho là: $x = k2\pi ;\,\,x = \, \pm \arccos \dfrac{{ - 1 \pm \sqrt 5 }}{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)$.

$\begin{array}{l}\,\,\,\,\,{\sin ^2}x + \sin 2x\sin 4x + \sin 3x\sin 9x + \sin 4x\sin 16x = 1\\ \Leftrightarrow {\sin ^2}x - \dfrac{1}{2}\left( {\cos 6x - \cos 2x} \right) - \dfrac{1}{2}\left( {\cos 12x - \cos 6x} \right) - \dfrac{1}{2}\left( {\cos 20x - \cos 12x} \right) = 1\\ \Leftrightarrow 2{\sin ^2}x - \cos 6x + \cos 2x - \cos 12x + \cos 6x - \cos 20x + \cos 12x = 2\\ \Leftrightarrow 2{\sin ^2}x + \cos 2x - \cos 20x = 2\\ \Leftrightarrow 1 - \cos 2x + \cos 2x - \cos 20x = 2\\ \Leftrightarrow \cos 20x =  - 1\\ \Leftrightarrow 20x = \pi  + k2\pi \\ \Leftrightarrow x = \dfrac{\pi }{{20}} + \dfrac{{k\pi }}{{10}}\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy nghiệm của phương trình là $x = \dfrac{\pi }{{20}} + \dfrac{{k\pi }}{{10}}\,\,\,\left( {k \in \mathbb{Z}} \right)$.

$\begin{array}{l}\,\,\,\,\,\cos 11x\cos 3x = \cos 17x\cos 9x\\ \Leftrightarrow \dfrac{1}{2}\left( {\cos 14x + \cos 8x} \right) = \dfrac{1}{2}\left( {\cos 26x + \cos 8x} \right)\\ \Leftrightarrow \cos 14x + \cos 8x = \cos 26x + \cos 8x\\ \Leftrightarrow \cos 14x = \cos 26x\\ \Leftrightarrow \left[ \begin{array}{l}26x = 14x + k2\pi \\26x =  - 14x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}12x = k2\pi \\40x = k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{6}\\x = \dfrac{{k\pi }}{{20}}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy nghiệm của phương trình là $x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\,\,\left( {k \in \mathbb{Z}} \right)$.

$\begin{array}{l}\,\,\,\,\,\,2{\sin ^2}2x + \sin 7x - 1 = \sin x\\ \Leftrightarrow \left( {2{{\sin }^2}2x - 1} \right) + \sin 7x - \sin x = 0\\ \Leftrightarrow  - \cos 4x + 2\cos 4x\sin 3x = 0\\ \Leftrightarrow \cos 4x\left( {2\sin 3x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos 4x = 0\\\sin 3x = \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}4x = \dfrac{\pi }{2} + k\pi \\3x = \dfrac{\pi }{6} + k2\pi \\3x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\\x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\\x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\end{array} \right.\end{array}$

Vậy nghiệm của phương trình là: $x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}$, $x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}$, $x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}$.

$\begin{array}{l}\,\,\,\,\,\,\cos 10x - \cos 8x - \cos 6x + 1 = 0\\ \Leftrightarrow \left( {\cos 10x - \cos 6x} \right) + \left( {1 - \cos 8x} \right) = 0\\ \Leftrightarrow  - 2\sin 8x\sin 2x + 2{\sin ^2}4x = 0\\ \Leftrightarrow  - 4\sin 4x\cos 4x\sin 2x + 2{\sin ^2}4x = 0\\ \Leftrightarrow 2\sin 4x\left( { - 2\cos 4x\sin 2x + \sin 4x} \right) = 0\\ \Leftrightarrow 2\sin 4x\left( { - 2\cos 4x\sin 2x + 2\sin 2x\cos 2x} \right) = 0\\ \Leftrightarrow 4\sin 4x.\sin 2x\left( { - \cos 4x + \cos 2x} \right) = 0\\ \Leftrightarrow 8{\sin ^2}2x\cos 2x\left( { - \cos 4x + \cos 2x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\\cos 2x = 0\\\cos 4x = \cos 2x\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = k\pi \\2x = \dfrac{\pi }{2} + k\pi \\4x = 2x + k2\pi \\4x =  - 2x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{2}\\x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\\x = k\pi \\x = \dfrac{{k\pi }}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{4}\\x = \dfrac{{k\pi }}{3}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy nghiệm của phương trình là: $x = \dfrac{{k\pi }}{4}$, $x = \dfrac{{k\pi }}{3}$.

$\begin{array}{l}\,\,\,\,\,\,\sin x + \sin 2x + \sin 3x + \sin 4x + \sin 5x + \sin 6x = 0\\ \Leftrightarrow \left( {\sin x + \sin 6x} \right) + \left( {\sin 2x + \sin 5x} \right) + \left( {\sin 3x + \sin 4x} \right) = 0\\ \Leftrightarrow 2\sin \dfrac{{7x}}{2}\cos \dfrac{{5x}}{2} + 2\sin \dfrac{{7x}}{2}\cos \dfrac{{3x}}{2} + 2\sin \dfrac{{7x}}{2}\cos \dfrac{x}{2} = 0\\ \Leftrightarrow 2\sin \dfrac{{7x}}{2}\left( {\cos \dfrac{{5x}}{2} + \cos \dfrac{{3x}}{2} + \cos \dfrac{x}{2}} \right) = 0\\ \Leftrightarrow 2\sin \dfrac{{7x}}{2}\left[ {2\cos \dfrac{{3x}}{2}\cos x + \cos \dfrac{{3x}}{2}} \right] = 0\\ \Leftrightarrow 2\sin \dfrac{{7x}}{2}.\cos \dfrac{{3x}}{2}\left( {2\cos x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin \dfrac{{7x}}{2} = 0\\\cos \dfrac{{3x}}{2}\\\cos x =  - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\dfrac{{7x}}{2} = k\pi \\\dfrac{{3x}}{2} = \dfrac{\pi }{2} + k\pi \\x =  \pm \dfrac{{2\pi }}{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k2\pi }}{7}\\x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\\x =  \pm \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\end{array}$

Vậy nghiệm của phương trình là: $x = \dfrac{{k2\pi }}{7}$, $x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}$, $x =  \pm \dfrac{{2\pi }}{3} + k2\pi$.

$\begin{array}{l}\,\,\,\,\,\cos x + \cos 2x + \cos 3x + \cos 4x = 0\\ \Leftrightarrow \left( {\cos x + \cos 3x} \right) + \left( {\cos 2x + \cos 4x} \right) = 0\\ \Leftrightarrow 2\cos 2x\cos x + 2\cos 3x\cos x = 0\\ \Leftrightarrow 2\cos x\left( {\cos 2x+\cos 3x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\\cos 3x = \cos (\pi-2x)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\3x = \pi-2x + k2\pi \\3x =   2x-\pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x =\dfrac{{\pi }}{5}+\dfrac{{k2\pi }}{5}\\x =-\pi+ k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy nghiệm của phương trình là: $x = \dfrac{\pi }{2} + k\pi$, $x =\dfrac{{\pi }}{5}+ \dfrac{{k2\pi }}{5}$, $x =-\pi+ k2\pi$.

 $\begin{array}{l}\,\,\,\,\,1 + \cos x + \cos 2x + \cos 3x = 0\\ \Leftrightarrow \left( {1 + \cos 2x} \right) + \left( {\cos x + \cos 3x} \right) = 0\\ \Leftrightarrow 2{\cos ^2}x + 2\cos 2x\cos x = 0\\ \Leftrightarrow 2\cos x\left( {\cos x + \cos 2x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\\cos x + \cos 2x = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\\cos 2x =  - \cos x = \cos \left( {\pi  - x} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\2x = \pi  - x + k2\pi \\2x = x - \pi  + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\3x = \pi  + k2\pi \\x =  - \pi  + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\\x =  - \pi  + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\end{array} \right.\end{array}$

Vậy nghiệm của phương trình là: $x = \dfrac{\pi }{2} + k\pi$, $x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}$.

Bước 1:

Điều kiện : $\sin x \ne 0 \Leftrightarrow x \ne k\pi$.

Bước 2:

Khi đó, phương trình $\Leftrightarrow \sin 5x = 2\sin x\cos x \Leftrightarrow \sin 5x = \sin 2x$

$\Leftrightarrow \left[ \begin{array}{l}5x = 2x + k2\pi \\5x = \pi  - 2x + k2\pi \end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}3x = k2\pi \\7x = \pi  + k2\pi \end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k2\pi }}{3}\\x = \dfrac{\pi }{7} + \dfrac{{k2\pi }}{7}\end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Bước 3:

Nếu $x = \dfrac{{k2\pi }}{3}$ thì $x \in \left( {0;\pi } \right) \Rightarrow 0 < \dfrac{{k2\pi }}{3} < \pi$$\Leftrightarrow 0 < k < \dfrac{3}{2} \Rightarrow k = 1 \Rightarrow x = \dfrac{{2\pi }}{3}\left( {TM} \right)$$\Rightarrow$ Có 1 nghiệm.

Nếu $x = \dfrac{\pi }{7} + \dfrac{{k2\pi }}{7}$ thì $x \in \left( {0;\pi } \right) \Rightarrow 0 < \dfrac{\pi }{7} + \dfrac{{k2\pi }}{7} < \pi$$\Leftrightarrow 0 < \pi  + k2\pi  < 7\pi  \Leftrightarrow  - \dfrac{1}{2} < k < 3$

$\Rightarrow k \in \left\{ {0;1;2} \right\} \Rightarrow x \in \left\{ {\dfrac{\pi }{7};\dfrac{{3\pi }}{7};\dfrac{{5\pi }}{7}} \right\}$$\Rightarrow$ Có 3 nghiệm.

Bước 4:

Vậy phương trình đã cho có $4$ nghiệm trong khoảng $\left( {0;\pi } \right)$.

Bước 1:

Ta có $\left( {2m + 1} \right){\rm{co}}{{\rm{s}}^2}2x - \left( {3m - 1} \right)\sin 2x - 3m + 1 = 0\,\,\left( * \right)$.

Đặt $t = \sin 2x \Rightarrow  - 1 \le t \le 1\left( {x \in \left( { - \pi ;\pi } \right)} \right)$

Bước 2:

Khi đó phương trình (*) có dạng:

$\begin{array}{l}\left( {2m + 1} \right)\left( {1 - {t^2}} \right) - \left( {3m - 1} \right)t - 3m + 1 = 0\\ \Leftrightarrow \left( {2m + 1} \right){t^2} + \left( {3m - 1} \right)t + m - 2 = 0\\ \Leftrightarrow \left( {t + 1} \right)\left( {\left( {2m + 1} \right)t + m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\\left( {2m + 1} \right)t + m - 2 = 0\end{array} \right.\end{array}$

Bước 3:

Nếu: $t =  - 1\,\,\,\left( {tm} \right) \Rightarrow \sin 2x =  - 1$

$\begin{array}{l} \Leftrightarrow 2x = \dfrac{{ - \pi }}{2} + k2\pi \left( {k \in {\rm Z}} \right)\\ \Leftrightarrow x = \dfrac{{ - \pi }}{4} + k\pi  \in \left( { - \pi ;\pi } \right)\\ \Rightarrow \dfrac{{ - 3}}{4} < k < \dfrac{5}{4} \Rightarrow k \in \left\{ {0;1} \right\}\end{array}$

Khi đó phương trình (*) có 2 nghiệm phân biệt là $\dfrac{{ - \pi }}{4};\dfrac{{3\pi }}{4}$

Bước 4:

$\left( {2m + 1} \right)t = 2 - m\,\,\left( 1 \right)$.

+) Nếu $m = \dfrac{{ - 1}}{2}$

Từ $(1) \Rightarrow m = 2\left( {ktm} \right)$

+) $m \ne \dfrac{{ - 1}}{2} \Rightarrow t = \dfrac{{2 - m}}{{2m + 1}}$

Để phương trình (*) có 2 nghiệm phân biệt thì

$\left[ \begin{array}{l}t = \dfrac{{2 - m}}{{2m + 1}} =  - 1\\t <  - 1\\t > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m =  - 3\\\dfrac{{m + 3}}{{2m + 1}} < 0 \Leftrightarrow  - 3 < m < \dfrac{{ - 1}}{2} \Leftrightarrow m \in \left\{ { - 2; - 1} \right\}\\\dfrac{{3m - 1}}{{2m + 1}} < 0 \Leftrightarrow \dfrac{{ - 1}}{2} < m < \dfrac{1}{3} \Leftrightarrow m = 0\end{array} \right.$

Vậy có 4 giá trị của $m$ thỏa mãn.