Tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(4\left( {{{\sin }^4}x + {{\cos }^4}x} \right) + {\sin ^2}2x + 4m\)\( = 4\cos 2x\) có nghiệm là đoạn $[a ; b]$. Tính \(2b - a\).

Bước 1: Đưa phương trình về dạng \(f\left( {\cos 2x} \right) = g\left( m \right)\)

Ta có: \(4\left( {{{\sin }^4}x + {{\cos }^4}x} \right) + {\sin ^2}2x + 4m\)\( = 4\cos 2x\)

\( \Leftrightarrow 4\left[ {{{\left( {{{\sin }^2}x + {{\cos }^2}x} \right)}^2} - 2{{\sin }^2}x{{\cos }^2}x} \right]\)\( + {\sin ^2}2x - 4\cos 2x + 4m = 0\)

\( \Leftrightarrow 4 - {\sin ^2}2x - 4\cos 2x + 4m = 0\)\( \Leftrightarrow {\cos ^2}2x - 4\cos 2x =  - 4m - 3\)

Bước 2: Đặt \(t = \cos 2x(t \in [ - 1;1])\). Đưa vế phải hàm đa thức biến t và khảo sát hàm số.

Đặt \(t = \cos 2x(t \in [ - 1;1])\). Ta có phương trình \({t^2} - 4t =  - 4m - 3(*)\) với \(t \in [ - 1;1]\).

Phương trình đã cho có nghiệm \(x\) khi và chỉ khi phương trình \((*)\) có nghiệm \(t \in [ - 1;1]\).

Lập bảng biến thiên của hàm \(f(t) = {t^2} - 4t\) trên \([ - 1;1]\).

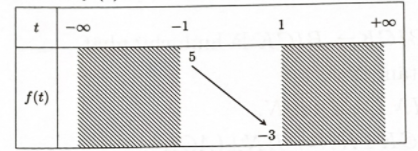
Từ bảng biến thiên ta thấy phương trình có nghiệm \(t \in [ - 1;1]\) khi và chỉ khi \( - 3 \le  - 4m - 3 \le 5 \Leftrightarrow  - 2 \le m \le 0\). Vậy \(a =  - 2;b = 0\) suy ra \(2b - a = 2\).