Cho phương trình \(\sin \left( {2x - \dfrac{\pi }{6}} \right) + 1 = 0\), nghiệm của phương trình là:
\(\begin{array}{l}\,\,\,\,\,\,\,\sin \left( {2x - \dfrac{\pi }{6}} \right) + 1 = 0 \Leftrightarrow \sin \left( {2x - \dfrac{\pi }{6}} \right) = - 1\\ \Leftrightarrow 2x - \dfrac{\pi }{6} = \dfrac{{ - \pi }}{2} + k2\pi \Leftrightarrow x = - \dfrac{\pi }{6} + k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Phương trình \(\tan x = 2\) có nghiệm là:
\(\tan x = 2 \Leftrightarrow x = \arctan 2 + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Số nghiệm của phương trình \(\tan x = \tan \dfrac{{3\pi }}{{11}}\) trên khoảng \(\left( {\dfrac{\pi }{4};2\pi } \right)\) là:
Ta có: \(\tan x = \tan \dfrac{{3\pi }}{{11}} \Leftrightarrow x = \dfrac{{3\pi }}{{11}} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Theo bài ra ta có:
\(\begin{array}{l}x \in \left( {\dfrac{\pi }{4};2\pi } \right)\\ \Rightarrow \dfrac{\pi }{4} < \dfrac{{3\pi }}{{11}} + k\pi < 2\pi \\ \Leftrightarrow - \dfrac{\pi }{{44}} < k\pi < \dfrac{{19\pi }}{{11}}\\ \Leftrightarrow - \dfrac{1}{{44}} < k < \dfrac{{19}}{{11}}\end{array}\)
Mà \(k \in \mathbb{Z}\) \( \Rightarrow k \in \left\{ {0;1} \right\}\).
Vậy phương trình đã cho có 2 nghiệm thỏa mãn yêu cầu bài toán.
Cho phương trình \(\cot x = \sqrt 3 \). Các nghiệm của phương trình là:
Ta có:\(\cot x = \sqrt 3 = \cot \dfrac{\pi }{6}\) \( \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Cho phương trình \(\tan 4x.\tan x = - 1\). Nghiệm của phương trình là:
ĐKXĐ: \(\left\{ \begin{array}{l}4x \ne \dfrac{\pi }{2} + k\pi \\x \ne \dfrac{\pi }{2} + k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\\x \ne \dfrac{\pi }{2} + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
\(\begin{array}{l}\tan 4x.\tan x = - 1\\ \Leftrightarrow \tan 4x = - \dfrac{1}{{\tan x}}\\ \Leftrightarrow \tan 4x = - \cot x\\ \Leftrightarrow \tan 4x = - \tan \left( {\dfrac{\pi }{2} - x} \right)\\ \Leftrightarrow \tan 4x = \tan \left( {x - \dfrac{\pi }{2}} \right)\\ \Leftrightarrow 4x = x - \dfrac{\pi }{2} + k\pi \\ \Leftrightarrow 3x = - \dfrac{\pi }{2} + k\pi \\ \Leftrightarrow x = - \dfrac{\pi }{6} + \dfrac{{k\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Đối chiếu điều kiện:
\(\begin{array}{l} + )\,\, - \dfrac{\pi }{6} + \dfrac{{k\pi }}{3} \ne \dfrac{\pi }{8} + \dfrac{{m\pi }}{4}\\ \Leftrightarrow - 4 + 8k \ne 3 + 6m\end{array}\)
Luôn đúng vì \( - 4 + 8k\) là số chẵn và \(3 + 6m\) là số lẻ \(\left( {m,\,\,k \in \mathbb{Z}} \right)\).
\(\begin{array}{l} + )\,\, - \dfrac{\pi }{6} + \dfrac{{k\pi }}{3} \ne \dfrac{\pi }{2} + m\pi \\ \Leftrightarrow - 1 + 2k \ne 3 + 6m\\ \Leftrightarrow k \ne 2 + 3m\,\,\left( {m \in Z} \right)\end{array}\)
Vậy nghiệm của phương trình là \( - \dfrac{\pi }{6} + k\dfrac{\pi }{3}\,\,\left( {k \in \mathbb{Z},\,\,k \ne 2 + 3m,\,m \in \mathbb{Z}} \right)\)
Phươg trình \({\tan ^2}x = 3\) có nghiệm là:
Ta có: \({\tan ^2}x = 3 \Leftrightarrow \left[ \begin{array}{l}\tan x = \sqrt 3 \\\tan x = - \sqrt 3 \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{3} + k\pi \\x = - \dfrac{\pi }{3} + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
Phương trình \(\tan x = \sqrt 3 \) có bao nhiêu nghiệm thuộc khoảng \(\left( { - 2017\pi ;2017\pi } \right)\)?
Ta có: \(\tan x = \sqrt 3 \Leftrightarrow x = \dfrac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(\begin{array}{l} - 2017\pi \le \dfrac{\pi }{3} + k\pi \le 2017\pi \\ \Leftrightarrow - 2017 \le \dfrac{1}{3} + k \le 2017\\ \Leftrightarrow - \dfrac{{6052}}{3} \le k \le \dfrac{{6050}}{3}\end{array}\)
Mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ { - 2017; - 2016;...;2015;2016} \right\}\).
Vậy có tất cả 2017 + 2016 + 1 = 4034 nghiệm thỏa mãn.
Số nghiệm \(x \in \left[ {0;12\pi } \right]\) của phương trình \(\tan \dfrac{x}{4} = - 1\) là:
\(\tan \dfrac{x}{4} = - 1 \Leftrightarrow \dfrac{x}{4} = \dfrac{{ - \pi }}{4} + k\pi \Leftrightarrow x = - \pi + 4k\pi \,\,\left( {k \in Z} \right)\)
\(x \in \left[ {0;12\pi } \right] \Leftrightarrow 0 \le - \pi + 4k\pi \le 12\pi \Leftrightarrow \dfrac{1}{4} \le k \le \dfrac{{13}}{4}\,\,\left( {k \in Z} \right) \Leftrightarrow k \in \left\{ {1;2;3} \right\}\).
Vậy phương trình đã cho có 3 nghiệm thuộc \(\left[ {0;12\pi } \right]\).
Tìm nghiệm của phương trình \(\cot \left( {x - \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{3}\).
Ta có: \(\cot \left( {x - \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{3} \Leftrightarrow x - \dfrac{\pi }{3} = \dfrac{\pi }{3} + k\pi \Leftrightarrow x = \dfrac{{2\pi }}{3} + k\pi \,\,\left( {k \in Z} \right)\).
Nghiệm của phương trình \(\cot \left( {x - 3} \right) = 4\) là:
\(\cot \left( {x - 3} \right) = 4 \Leftrightarrow x - 3 = {\mathop{\rm arccot}\nolimits} 4 + k\pi \Leftrightarrow x = 3 + {\mathop{\rm arccot}\nolimits} 4 + k\pi \,\,\left( {k \in Z} \right)\).
Nghiệm của phương trình \(\tan x = \tan 3x\) là:
Bước 1:
=>ĐK:
\(\left\{ {\begin{array}{*{20}{l}}{\cos x \ne 0}\\{\cos 3x \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\cos x \ne 0}\\{4{{\cos }^3}x - 3\cos x \ne 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\cos x \ne 0\\\cos x\left( {4{{\cos }^2}x - 3} \right) \ne 0\end{array} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\cos x \ne 0}\\{4{{\cos }^2}x - 3 \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\cos x \ne 0}\\{2.\left( {\cos 2x + 1} \right) - 3 \ne 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\cos x \ne 0}\\{2.\cos 2x - 1 \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\cos x \ne 0}\\{\cos 2x \ne \dfrac{1}{2}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne \dfrac{\pi }{2} + k\pi }\\{2x \ne \pm \dfrac{\pi }{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{2} + k\pi (*)\\x \ne \pm \dfrac{\pi }{6} + k\pi \end{array} \right.\)
Bước 2:
\(\tan x = \tan 3x \Leftrightarrow 3x = x + k\pi \Leftrightarrow 2x = k\pi \Leftrightarrow x = \dfrac{{k\pi }}{2}\,\,\left( {k \in Z} \right)\).
Với k chẵn, tức là \(k=2m\) thì \(x = m\pi \,\,\left( {m \in Z} \right)\) (TMĐK) => Nhận.
Với k lẻ, tức là \(k=2m+1\) thì \(x =\dfrac{(2m+1)\pi}{2} \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \,\,\left( {m \in Z} \right)\) (Mâu thuẫn với (*))=> Loại.
=>\(x = m\pi \,\,\left( {m \in Z} \right)\).
Vai trò của m lúc này như vai trò của k nên ta có thể viết \(x = k\pi \,\,\left( {k \in Z} \right)\).
Số nghiệm của phương trình \(\cos \left( {x - \dfrac{\pi }{3}} \right) = \cos \left( {2x + \dfrac{\pi }{6}} \right)\) trên \(\left( { - \pi ;\pi } \right)\) là.
TXĐ: \(D = \mathbb{R}\).
\(\begin{array}{l}\cos \left( {x - \dfrac{\pi }{3}} \right) = \cos \left( {2x + \dfrac{\pi }{6}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{6} = x - \dfrac{\pi }{3} + k2\pi \\2x + \dfrac{\pi }{6} = - x + \dfrac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{2} + k2\pi \\x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Xét họ nghiệm \(x = - \dfrac{\pi }{2} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\), cho \(x \in \left( { - \pi ;\pi } \right)\).
\(\begin{array}{l} \Rightarrow - \pi < - \dfrac{\pi }{2} + k2\pi < \pi \\ \Leftrightarrow - 1 < - \dfrac{1}{2} + 2k < 1\\ \Leftrightarrow - \dfrac{1}{4} < k < \dfrac{3}{4}\end{array}\)
Mà \(k \in \mathbb{Z} \Rightarrow k = 0\)\( \Rightarrow x = - \dfrac{\pi }{2}\).
Xét họ nghiệm \(x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\,\,\,\left( {k \in \mathbb{Z}} \right)\), cho \(x \in \left( { - \pi ;\pi } \right)\).
\(\begin{array}{l} \Rightarrow - \pi < \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3} < \pi \\ \Leftrightarrow - 1 < \dfrac{1}{{18}} + \dfrac{{2k}}{3} < 1\\ \Leftrightarrow - \dfrac{{19}}{{12}} < k < \dfrac{{17}}{{12}}\end{array}\)
Mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ { - 1;0;1} \right\}\)\( \Rightarrow x \in \left\{ { - \dfrac{{11\pi }}{{18}};\dfrac{\pi }{{18}};\dfrac{{13\pi }}{{18}}} \right\}\).
Vậy phương trình đã cho có 4 nghiệm thuộc \(\left( { - \pi ;\pi } \right)\).
Tìm số nghiệm trong khoảng \(\left( { - \pi ;\pi } \right)\) của phương trình \(\sin x = \cos 2x\).
Bước 1:
Ta có : \(\sin x = \cos 2x\)
$\Leftrightarrow \cos \left( {\dfrac{\pi }{2} - x} \right) = \cos 2x$
Bước 2:
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{2} - x + k2\pi \\2x = x - \dfrac{\pi }{2} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3}\\x = - \dfrac{\pi }{2} + k2\pi \end{array} \right.\end{array}\)
Bước 3:
Vì \(x \in \left( { - \pi ;\pi } \right)\)
Xét \(x = \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3}\)
\( - \pi \le \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3} \le \pi \)\( \Leftrightarrow - \dfrac{{7\pi }}{6} \le \dfrac{{k2\pi }}{3} \le \dfrac{{5\pi }}{6}\)
\( \Leftrightarrow - \dfrac{7}{4} \le k \le \dfrac{5}{4} \Leftrightarrow \left[ \begin{array}{l}k = - 1\\k = 0\\k = 1\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} - \dfrac{{2\pi }}{3} = - \dfrac{\pi }{2}\\x = \dfrac{\pi }{6}\\x = \dfrac{\pi }{6} + \dfrac{{2\pi }}{3} = \dfrac{{5\pi }}{6}\end{array} \right.\)
Xét \(x = - \dfrac{\pi }{2} + k2\pi \)
\( \Rightarrow - \pi \le - \dfrac{\pi }{2} + k2\pi \le \pi \)\( \Leftrightarrow - \dfrac{\pi }{2} \le k2\pi \le \dfrac{{3\pi }}{2}\)
\( \Leftrightarrow - \dfrac{1}{4} \le k \le \dfrac{{3\pi }}{4} \Leftrightarrow k = 0 \Rightarrow x = - \dfrac{\pi }{2}\)
=> \(x \in \left\{ {\dfrac{\pi }{6};\dfrac{{5\pi }}{6}; - \dfrac{\pi }{2}} \right\}\)
Vậy có 3 nghiệm thỏa mãn đề bài.
Số nghiệm của phương trình \(\sqrt 2 \cos \left( {x + \dfrac{\pi }{3}} \right) = 1\) với \(0 \le x \le 2\pi \) là
Ta có \(\sqrt 2 \cos \left( {x + \dfrac{\pi }{3}} \right) = 1 \Leftrightarrow \cos \left( {x + \dfrac{\pi }{3}} \right) = \dfrac{1}{{\sqrt 2 }}\)
\( \Leftrightarrow \cos \left( {x + \dfrac{\pi }{3}} \right) = \cos \dfrac{\pi }{4} \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{3} = - \dfrac{\pi }{4} + k2\pi \end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{12}} + k2\pi \\x = - \dfrac{{7\pi }}{{12}} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)
Nếu \(x = - \dfrac{\pi }{{12}} + k2\pi \) thì \(x \in \left[ {0;2\pi } \right] \Rightarrow 0 \le - \dfrac{\pi }{{12}} + k2\pi \le 2\pi \Leftrightarrow \dfrac{1}{{24}} \le k \le \dfrac{{25}}{{24}} \Rightarrow k = 1 \Rightarrow x = \dfrac{{23\pi }}{{12}}\).
Nếu \(x = - \dfrac{{7\pi }}{{12}} + k2\pi \) thì \(x \in \left[ {0;2\pi } \right] \Rightarrow 0 \le - \dfrac{{7\pi }}{{12}} + k2\pi \le 2\pi \Leftrightarrow \dfrac{7}{{24}} \le k \le \dfrac{{31}}{{24}} \Rightarrow k = 1 \Rightarrow x = \dfrac{{17\pi }}{{12}}\).
Vậy có hai giá trị của \(x\) thỏa mãn đề bài.
Nghiệm của phương trình \(2\cos x + 1 = 0\) là:
Bước 1:
Ta có : \(2\cos x + 1 = 0 \Leftrightarrow \cos x = - \dfrac{1}{2}\).
Bước 2:
\( \Leftrightarrow \cos x = \cos \dfrac{{2\pi }}{3}\)
Bước 3:
\( \Leftrightarrow x = \pm \dfrac{{2\pi }}{3} + k2\pi ,,k \in \mathbb{Z}\)
Bước 4:
Vậy nghiệm của phương trình là \(x = \pm \dfrac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\)
Xác định \(m\) để phương trình \(\tan \dfrac{x}{2} = \dfrac{m}{{1 - 2m}}\,\,\left( {m \ne \dfrac{1}{2}} \right)\) có nghiệm \(x \in \left( {\dfrac{\pi }{2};\pi } \right)\).
Bước 1:
ĐK: \(\dfrac{x}{2} \ne \dfrac{\pi }{2} + k\pi \Leftrightarrow x \ne \pi + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Với \(x \in \left( {\dfrac{\pi }{2};\pi } \right) \Rightarrow \dfrac{x}{2} \in \left( {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right)\).
Do hàm số \(y = \tan X\) đồng biến trên \(\left( {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right)\) nên khi $X=\dfrac{x}{2}$ ta có:
\(\dfrac{\pi }{4} < \dfrac{x}{2} < \dfrac{\pi }{2} \Leftrightarrow \tan \dfrac{\pi }{4} < \tan \dfrac{x}{2} < \tan \dfrac{\pi }{2} \Leftrightarrow 1 < \tan \dfrac{x}{2} < + \infty \).
Đồ thị của hàm số: Khi x tăng dần đến $\dfrac{\pi }{2}$ thì hàm số cũng tăng dần đến \(+ \infty \).
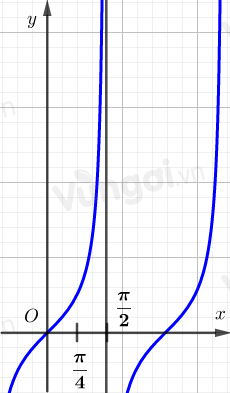
Như thế ta có $ \tan \dfrac{x}{2}>1$.
Bước 2:
Suy ra phương trình \(\tan \dfrac{x}{2} = \dfrac{m}{{1 - 2m}}\,\,\left( {m \ne \dfrac{1}{2}} \right)\) có nghiệm khi và chỉ khi
\(\dfrac{m}{{1 - 2m}} > 1 \Leftrightarrow \dfrac{m}{{1 - 2m}} - 1 > 0\)\( \Leftrightarrow \dfrac{{m - 1 + 2m}}{{1 - 2m}} > 0 \)\(\Leftrightarrow \dfrac{{3m - 1}}{{1 - 2m}} > 0 \Leftrightarrow \dfrac{1}{3} < m < \dfrac{1}{2}\)
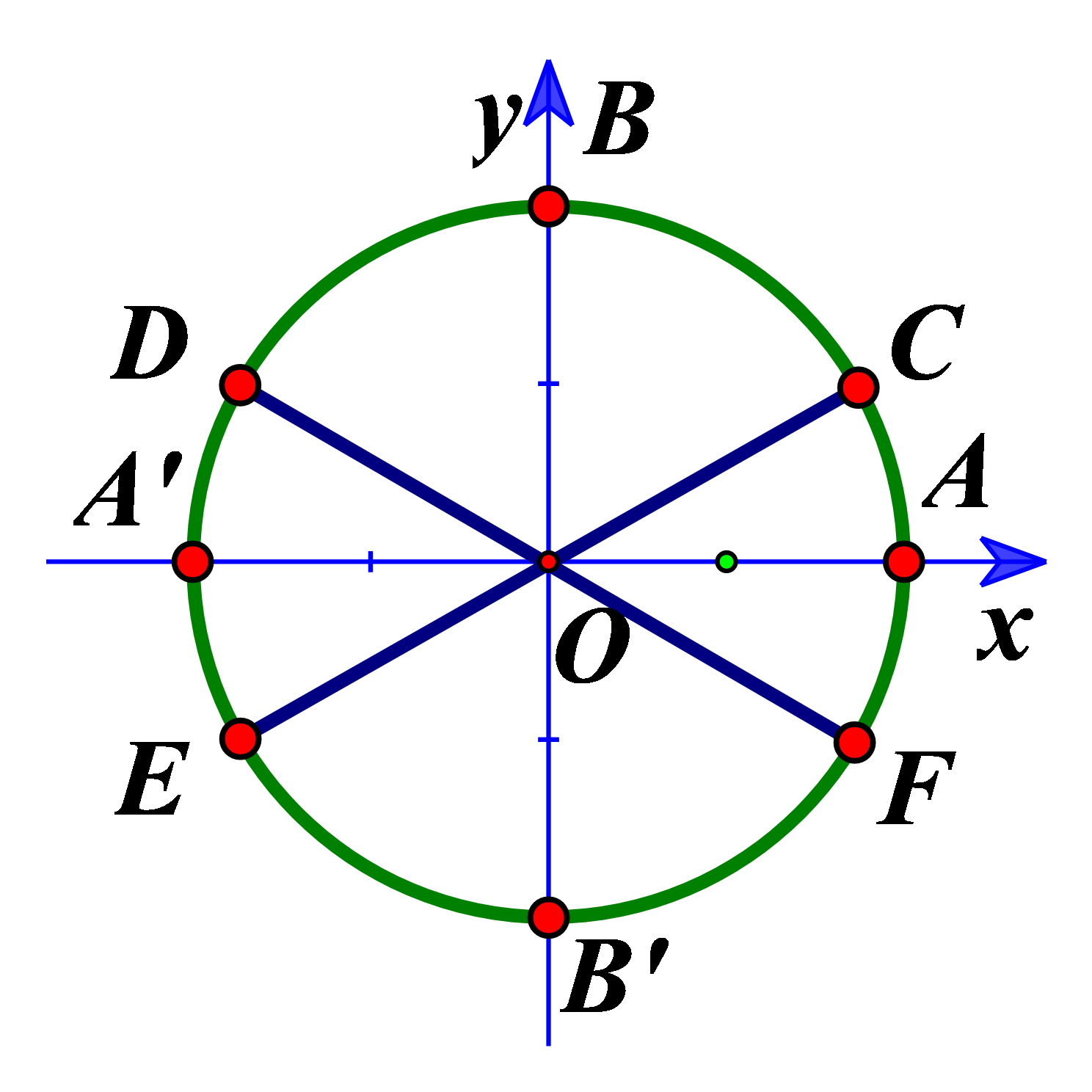
Nghiệm của phương trình \(2\sin x + 1 = 0\) được biểu diễn trên đường tròn lượng giác ở hình trên là những điểm nào?
Bước 1: Tìm x
Ta có \(2\sin x + 1 = 0 \Leftrightarrow \sin x = - \dfrac{1}{2}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - \dfrac{\pi }{6} + k2\pi }\\{x = \dfrac{{7\pi }}{6} + k2\pi }\end{array}(k \in \mathbb{Z})} \right.\).
Bước 2: Tìm k từ đó tìm các điểm biểu diễn.
Với \(k = 0 \Rightarrow x = - \dfrac{\pi }{6}\) hoặc \(x = \dfrac{{7\pi }}{6}\).
Điểm biểu diễn của \(x = - \dfrac{\pi }{6}\) là \(F\), điểm biểu diễn \(x = \dfrac{{7\pi }}{6}\) là \(E\).
Nghiệm của phương trình $\sin x = 1$ là:
$\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi ,{\rm{ }}k \in \mathbb{Z}$.
Nghiệm của phương trình \(\tan 2x + \sqrt 3 = 0\) là:
\(\tan 2x + \sqrt 3 = 0 \Leftrightarrow \tan 2x = - \sqrt 3 \Leftrightarrow 2x = - \dfrac{\pi }{3} + k\pi \Leftrightarrow x = - \dfrac{\pi }{6} + k\dfrac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
Nghiệm của phương trình $\cos x = 1$ là:
$\cos x = 1 \Leftrightarrow x = k2\pi ,{\rm{ }}k \in \mathbb{Z}$.

