Xác định $m$ để phương trình $\tan \dfrac{x}{2} = \dfrac{m}{{1 - 2m}}\,\,\left( {m \ne \dfrac{1}{2}} \right)$ có nghiệm $x \in \left( {\dfrac{\pi }{2};\pi } \right)$.

Bước 1:

ĐK: $\dfrac{x}{2} \ne \dfrac{\pi }{2} + k\pi  \Leftrightarrow x \ne \pi  + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)$.

Với $x \in \left( {\dfrac{\pi }{2};\pi } \right) \Rightarrow \dfrac{x}{2} \in \left( {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right)$.

Do hàm số $y = \tan X$ đồng biến trên $\left( {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right)$ nên khi $X=\dfrac{x}{2}$ ta có:

$\dfrac{\pi }{4} < \dfrac{x}{2} < \dfrac{\pi }{2} \Leftrightarrow \tan \dfrac{\pi }{4} < \tan \dfrac{x}{2} < \tan \dfrac{\pi }{2} \Leftrightarrow 1 < \tan \dfrac{x}{2} <  + \infty$.

Đồ thị của hàm số: Khi x tăng dần đến $\dfrac{\pi }{2}$ thì hàm số cũng tăng dần đến $+ \infty$.

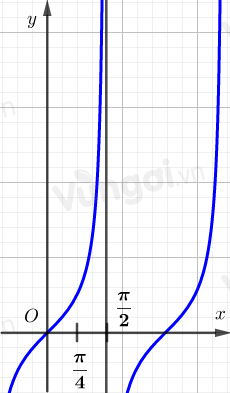
Như thế ta có $\tan \dfrac{x}{2}>1$.

Bước 2:

Suy ra phương trình $\tan \dfrac{x}{2} = \dfrac{m}{{1 - 2m}}\,\,\left( {m \ne \dfrac{1}{2}} \right)$ có nghiệm khi và chỉ khi

$\dfrac{m}{{1 - 2m}} > 1 \Leftrightarrow \dfrac{m}{{1 - 2m}} - 1 > 0$$\Leftrightarrow \dfrac{{m - 1 + 2m}}{{1 - 2m}} > 0$$\Leftrightarrow \dfrac{{3m - 1}}{{1 - 2m}} > 0 \Leftrightarrow \dfrac{1}{3} < m < \dfrac{1}{2}$