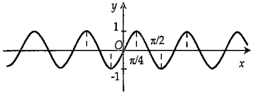
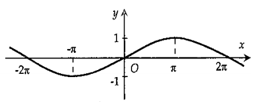
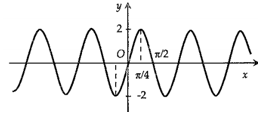
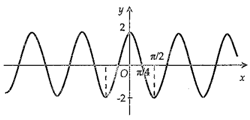
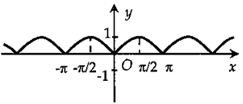
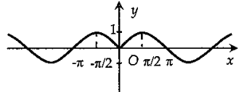
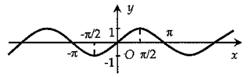
Tập xác định của hàm số \(y = \dfrac{1}{{2\cos x - 1}}\) là:
Hàm số đã cho xác định khi:
\(2\cos x - 1 \ne 0 \Leftrightarrow \cos x \ne \dfrac{1}{2}\)\( \Leftrightarrow x \ne \pm \dfrac{\pi }{3} + k2\pi \) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{3} + k2\pi \\x \ne - \dfrac{\pi }{3} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x \ne \dfrac{{5\pi }}{3} + l2\pi ,l \in \mathbb{Z}\end{array} \right.\)
Tập xác định của hàm số \(y = \dfrac{{\cot x}}{{\sin x - 1}}\) là:
Hàm số đã cho xác định khi
\(\cot x\) xác định và $\sin x - 1 \ne 0$
\( \Leftrightarrow \left\{ \begin{array}{l}\sin x \ne 0\\\sin x \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne k\pi \\x \ne \dfrac{\pi }{2} + k2\pi \end{array} \right.,k \in \mathbb{Z}\)
Tập hợp \(\mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\) không phải là tập xác định của hàm số nào?
\(\cos 2x \ne 0 \Leftrightarrow 2x \ne \dfrac{\pi}{2}+k\pi \) \( \Leftrightarrow x \ne \dfrac{\pi}{4}+\dfrac{{k\pi }}{2},\,k \in \mathbb{Z}\)
Suy ra tập xác định của hàm số $y = \dfrac{{1 + \cos x}}{{\cos 2x}}$ là \(\mathbb{R}\backslash \left\{ {\dfrac{\pi}{4}+\dfrac{{k\pi }}{2},\,k \in \mathbb{Z}} \right\}\)\( \ne \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\)
Mà \(\sin x \ne 0 \Leftrightarrow x \ne k\pi ,\,k \in \mathbb{Z}\) nên tất cả các hàm số trong đáp án A, B, D đều có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\)
Tập xác định của hàm số \(y = \sqrt {1 - \cos 2017x} \) là
Hàm số \(y = \sqrt {1 - \cos 2017x} \) xác định khi \(1 - \cos 2017x \ge 0.\)
Mặt khác ta có \( - 1 \le \cos 2017x \le 1\) nên \(1 - \cos 2017x \ge 0,\,\forall x \in \mathbb{R}\).
Hàm số nào sau đây là hàm số chẵn?
Với các kiến thức về tính chẵn lẻ của hsố lượng giác cơ bản ta có thể chọn luôn A.
Xét A: Do tập xác định $D = \mathbb{R}$ nên $\forall x \in \mathbb{R} \Rightarrow - x \in \mathbb{R}$.
Ta có $f\left( { - x} \right) = - 2\cos \left( { - x} \right) = - 2\cos x = f\left( x \right)$.
Vậy hàm số $y = - 2\cos x$ là hàm số chẵn.
Cho hai hàm số $f\left( x \right) = \dfrac{1}{{x - 3}} + 3{\sin ^2}x$ và $g\left( x \right) = \sin \sqrt {1 - x} $. Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?
Xét hàm số $f\left( x \right) = \dfrac{1}{{x - 3}} + 3{\sin ^2}x$ có tập xác định là $D = \mathbb{R}\backslash \left\{ 3 \right\}$.
Ta có $x = - 3 \in D$ nhưng $ - x = 3 \notin D$ nên $D$ không có tính đối xứng. Do đó ta có kết luận hàm số $f\left( x \right)$ không chẵn không lẻ.
Xét hàm số $g\left( x \right) = \sin \sqrt {1 - x} $ có tập xác định là ${D_2} = \left[ {1; + \infty } \right)$. Dễ thấy ${D_2}$ không phải là tập đối xứng nên ta kết luận hàm số $g\left( x \right)$ không chẵn không lẻ.
Xác định tất cả các giá trị của tham số $m$ để hàm số \(y = f\left( x \right) = 3m\sin 4x +\cos 2x\) là hàm chẵn.
TXĐ: \(D = \mathbb{R}.\) Suy ra \(\forall x \in D \Rightarrow - x \in D.\)
Ta có \(f\left( { - x} \right) = 3m\,{\rm{sin4}}\left( { - x} \right) + \cos 2\left( { - x} \right) = - 3m\,{\rm{sin4}}x + \cos 2x.\)
Để hàm số đã cho là hàm chẵn thì
$\begin{array}{l}f\left( { - x} \right) = f\left( x \right),\,\forall x \in D \Leftrightarrow - 3m\,{\rm{sin4}}x + \cos 2x = 3m\,{\rm{sin4}}x + \cos 2x,\,\forall x \in D\\ \Leftrightarrow 6m\sin 4x = 0,\,\forall x \in D \Leftrightarrow m = 0.\end{array}$
Xét hàm số \(y = \sin \,x\) trên đoạn \(\left[ { - \pi ;\,0} \right].\) Khẳng định nào sau đây là đúng?
Từ bảng biến thiên của hàm số $y=\sin x$ trên $[-\pi ; \pi]$ ta có hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( { - \pi ;\, - \dfrac{\pi }{2}} \right)\) và đồng biến trên khoảng \(\,\,\left( { - \dfrac{\pi }{2};\,0} \right).\)
Chọn câu đúng?
Với A ta thấy hàm số \(y = \tan x\) không xác định tại mọi điểm \(x \in \mathbb{R}\) nên tồn tại các điểm làm cho hàm số bị gián đoạn nên hàm số không thể luôn tăng.
Với B ta thấy B đúng vì hàm số \(y = \tan x\) đồng biến trên mỗi khoảng \(\left( { - \dfrac{\pi }{2} + k\pi ;\,\dfrac{\pi }{2} + k\pi } \right),\,k \in \mathbb{Z}.\)
Từ đây loại C và D.
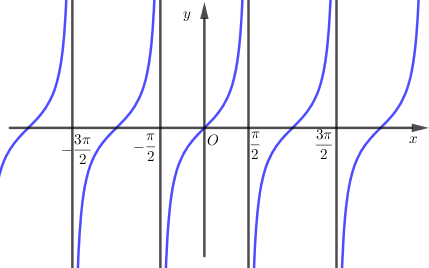
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: \(y = 2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) + 2016.\)
Hàm số xác định trên \(R\) .
Ta có \( - 1 \le \cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) \le 1,\forall x \in R.\)
\( \Leftrightarrow - 2017 \le 2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) \le 2017,\forall x \in \,R\)
\( \Leftrightarrow - 1 \le 2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) + 2016 \le 4033,\forall x \in \,R\)
Ta có \(y = - 1\) khi \(\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) = - 1\) ; \(y = 4033\) khi \(\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) = 1\)
Vậy \(\min y = - 1;\max y = 4033\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: \(y = 2{\cos ^2}x - 2\sqrt 3 \sin {\rm{x}}\cos x + 1\)
Ta có \(y = 2{\cos ^2}x - 2\sqrt 3 \sin {\rm{x}}\cos x + 1\) \( = 2{\cos ^2}x - 1 - \sqrt 3 \sin 2x + 2\)\( = \cos 2x - \sqrt 3 \sin 2x + 2\left( * \right)\)
Mà \( - \sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2}} \le \cos 2x - \sqrt 3 \sin 2x \le \sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2}} \)
Nên \( - 2 \le \cos 2x - \sqrt 3 \sin 2x \le 2\)
\( \Rightarrow 0 \le \cos 2x - \sqrt 3 \sin 2x + 2 \le 4\) hay \(0 \le y \le 4,\forall x \in \,R\)
Vậy \(\min y = 0;\max y = 4\)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3}}{{2 + \cos x}}\)
Bước 1:
Ta có \(\cos x + 2 > 0,\forall x \in \,R\) .
\(y = \dfrac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3}}{{2 + \cos x}}\) \( \Leftrightarrow {\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3 = 2y + y\cos x\) \( \Leftrightarrow {\mathop{\rm s}\nolimits} {\rm{inx}} + \left( {2 - y} \right)\cos x = 2y-3\,\left( * \right)\)
Bước 2:
Ta có điều kiện có nghiệm của phương trình \(\left( * \right)\) là:
\({1^2} + {\left( {2 - y} \right)^2} \ge {\left( {2y-3} \right)^2}\) \( \Leftrightarrow 4{y^2} - 12y + 9 - {y^2} + 4y - 4 - 1 \le 0\) \( \Leftrightarrow 3{y^2} - 8y + 4 \le 0\) \( \Leftrightarrow \dfrac{2}{3} \le y \le 2\)
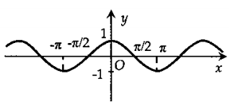
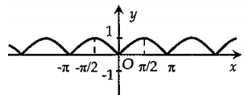
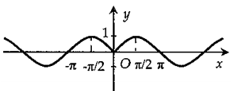
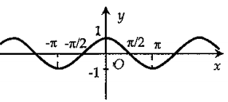
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f(x) = 2\sin 2x?\)
Ta thấy \( - 2 \le 2\sin 2x \le 2\) nên ta có loại A và B.
Tiếp theo với C và D ta có:
Từ phần lý thuyết ở trên ta có hàm số tuần hoàn với chu kì \(\dfrac{{2\pi }}{{\left| 2 \right|}} = \pi .\)
Ta thấy với \(x = 0\) thì \(y = 0\) nên đồ thị hàm số đi qua gốc tọa độ.
Cho đồ thị hàm số \(y = \sin x\) như hình vẽ:
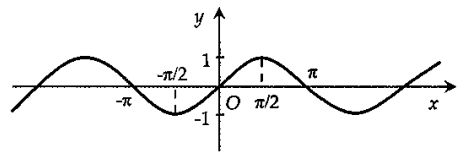
Hình nào sau đây là đồ thị hàm số \(y = \sin \left| x \right|?\)
Suy diễn đồ thị hàm số \(y = \sin |x|\) từ đồ thị hàm số \(y = \sin x:\)
Giữ nguyên phần đồ thị của hàm số \(y = \sin x\) nằm bên phải trục \(Oy.\)
Lấy đối xứng phần đồ thị trên qua trục \(Oy.\)
Dưới đây là đồ thị ta thu được sau khi thực hiện các bước suy diễn ở trên. Phần đồ thị nét đứt là phần bỏ đi của đồ thị hàm số \(y = \sin x.\)
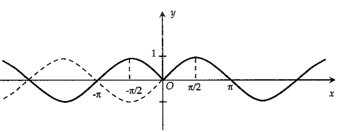
Hình nào sau đây là đồ thị hàm số \(y = \left| {\sin x} \right|?\)
Suy diễn đồ thị hàm số \(y = |\sin x|\) từ đồ thị hàm số \(y = \sin x:\)
Giữ nguyên phần tử từ trục hoành trở lên của đồ thị \(y = \sin x.\)
Lấy đối xứng phần đồ thị của hàm số \(y = \sin x\) phía dưới trục hoành qua trục hoành.
Số vị trí biểu diễn các nghiệm của phương trình \(\sin \left( {2x + \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\) trên đường tròn lượng giác là?
Phương trình \( \Leftrightarrow \sin \left( {2x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{3} = \dfrac{\pi }{6} + k2\pi \\2x + \dfrac{\pi }{3} = \pi - \dfrac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{\pi }{4} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\)
Biểu diễn nghiệm \(x = - \dfrac{\pi }{{12}} + k\pi \) trên đường tròn lượng giác ta được 2 vị trí (hình 1).
Biểu diễn nghiệm \(x = \dfrac{\pi }{4} + k\pi \) trên đường tròn lượng giác ta được 2 vị trí (hình 2).
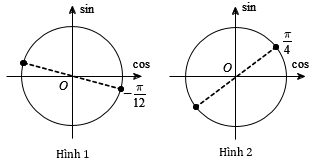
Vậy có tất cả 4 vị trí biểu diễn các nghiệm các nghiệm của phương trình.
Với những giá trị nào của \(x\) thì giá trị của các hàm số \(y = \sin 3x\) và \(y = \sin x\) bằng nhau?
Xét phương trình hoành độ giao điểm: \(\sin 3x = \sin x\)
\( \Leftrightarrow \left[ \begin{array}{l}3x = x + k2\pi \\3x = \pi - x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{4} + k\dfrac{\pi }{2}\end{array} \right.{\rm{ }}\left( {k \in \mathbb{Z}} \right).\)
Gọi \({x_0}\) là nghiệm dương nhỏ nhất của phương trình \(\dfrac{{2\cos 2x}}{{1 - \sin 2x}} = 0\). Mệnh đề nào sau đây là đúng?
Điều kiện: \(1 - \sin 2x \ne 0 \Leftrightarrow \sin 2x \ne 1.\)
Phương trình \(\dfrac{{2\cos 2x}}{{1 - \sin 2x}} = 0 \Leftrightarrow \cos 2x = 0 \Rightarrow \left[ \begin{array}{l}\sin 2x = 1\left( L \right)\\\sin 2x = - 1\left( {TM} \right)\end{array} \right.\)
\( \Leftrightarrow \sin 2x = - 1 \Leftrightarrow 2x = - \dfrac{\pi }{2} + k2\pi \Leftrightarrow x = - \dfrac{\pi }{4} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\)
Cho \( - \dfrac{\pi }{4} + k\pi > 0 \Rightarrow k > \dfrac{1}{4}\).
Do đó nghiệm dương nhỏ nhất ứng với \(k = 1 \to x = \dfrac{{3\pi }}{4} \in \left[ {\dfrac{{3\pi }}{4};\pi } \right].\)
Hỏi trên đoạn \(\left[ { - 2017;2017} \right]\), phương trình \(\left( {\sin x + 1} \right)\left( {\sin x - \sqrt 2 } \right) = 0\) có tất cả bao nhiêu nghiệm?
Phương trình \( \Leftrightarrow \left[ \begin{array}{l}\sin x = - 1\\\sin x = \sqrt 2 \left( {VN} \right)\end{array} \right.\)\( \Leftrightarrow \sin x = - 1\) \( \Leftrightarrow x = - \dfrac{\pi }{2} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\)
Theo giả thiết \( - 2017 \le - \dfrac{\pi }{2} + k2\pi \le 2017\)\( \Leftrightarrow \dfrac{{ - 2017 + \dfrac{\pi }{2}}}{{2\pi }} \le k \le \dfrac{{2017 + \dfrac{\pi }{2}}}{{2\pi }}\)
\( \Rightarrow - 320,765 \le k \le 321,265\)\( \Rightarrow k \in \left\{ { - 320; - 319;...;321} \right\}.\)
Vậy có tất cả \(642\) giá trị nguyên của \(k\) tương ứng với có \(642\) nghiệm thỏa mãn yêu cầu bài toán.
Tính tổng \(T\) các nghiệm của phương trình \(\sin 2x - \cos x = 0\) trên \(\left[ {0;2\pi } \right].\)
Ta có $\sin 2x - \cos x = 0 \Leftrightarrow \sin 2x = \cos x \Leftrightarrow \sin 2x = \sin \left( {\dfrac{\pi }{2} - x} \right)$
$ \Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{2} - x + k2\pi \\2x = \pi - \left( {\dfrac{\pi }{2} - x} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3}\\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.$.
Vì $x \in \left[ {0;2\pi } \right]$, suy ra $\left[ \begin{array}{l}0 \le \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3} \le 2\pi \\0 \le \dfrac{\pi }{2} + k2\pi \le 2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - \dfrac{1}{4} \le k \le \dfrac{{11}}{4} \Rightarrow k \in \left\{ {0;1;2} \right\}\\ - \dfrac{1}{4} \le k \le \dfrac{3}{4} \Rightarrow k \in \left\{ 0 \right\}\end{array} \right..$
Từ đó suy ra các nghiệm của phương trình trên đoạn \(\left[ {0;2\pi } \right]\) là $\dfrac{\pi }{6};\dfrac{{5\pi }}{6};\dfrac{{3\pi }}{2};\dfrac{\pi }{2} \to T = 3\pi .$