Bài tập ôn tập chương 1

Ta có $\cot \left( {3x - 1} \right) =  - \sqrt 3  \Leftrightarrow \cot \left( {3x - 1} \right) = \cot \left( { - \dfrac{\pi }{6}} \right)$

$ \Leftrightarrow 3x - 1 =  - \dfrac{\pi }{6} + k\pi  \Leftrightarrow x = \dfrac{1}{3} - \dfrac{\pi }{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right)$

Hay $x = \dfrac{1}{3} + \dfrac{{5\pi }}{{18}} + \dfrac{{l\pi }}{3},l \in \mathbb{Z}$

Phương trình \(\cos \left( {2x - \dfrac{\pi }{3}} \right) - m = 2 \Leftrightarrow \cos \left( {2x - \dfrac{\pi }{3}} \right) = m + 2.\)

Phương trình có nghiệm $ \Leftrightarrow  - \,1 \le m + 2 \le 1 \Leftrightarrow  - \,3 \le m \le  - \,1$

\( \Rightarrow S = \left\{ { - 3; - 2; - 1} \right\}\)\( \Rightarrow T = \left( { - 3} \right) + \left( { - 2} \right) + \left( { - 1} \right) =  - 6\)

Vì $x = \dfrac{\pi }{{12}}$ là một nghiệm của phương trình $\left( {m - 2} \right)\sin 2x = m + 1$ nên ta có:

$\left( {m - 2} \right).\sin \dfrac{{2\pi }}{{12}} = m + 1 \Leftrightarrow \dfrac{{m - 2}}{2} = m + 1 \Leftrightarrow m - 2 = 2m + 2 \Leftrightarrow m =  - \,4$.

Vậy $m =  - \,4$ là giá trị cần tìm.

TH1. Với $m = 2$, phương trình trở thành \(0 = 3\) vô nghiệm.

TH2. Với $m \ne 2$, phương trình $\left( {m - 2} \right)\sin 2x = m + 1 \Leftrightarrow \sin 2x = \dfrac{{m + 1}}{{m - 2}}.$

Để phương trình $\left(  *  \right)$ vô nghiệm $ \Leftrightarrow \dfrac{{m + 1}}{{m - 2}} \notin \left[ { - \,1;1} \right] \Leftrightarrow \left[ \begin{array}{l}\dfrac{{m + 1}}{{m - 2}} > 1\\\dfrac{{m + 1}}{{m - 2}} <  - \,1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 2\\\dfrac{1}{2} < m < 2\end{array} \right..$

Kết hợp hai trường hợp, ta được $m > \dfrac{1}{2}$ là giá trị cần tìm.

Bước 1:

Phương trình \( \Leftrightarrow (3\sin 3x - 4{\sin ^3}3x) - \sqrt 3 \cos 9x = 1\)\( \Leftrightarrow \sin 9x - \sqrt 3 \cos 9x = 1\)

Bước 2:

\( \Leftrightarrow \dfrac{1}{2}\sin 9x - \dfrac{{\sqrt 3 }}{2}\cos 9x = \dfrac{1}{2} \)

\( \Leftrightarrow \cos \left( {\dfrac{\pi }{3}} \right) \sin 9x - \sin \left( {\dfrac{\pi }{3}} \right)\cos 9x = \dfrac{1}{2} \)

\(\Leftrightarrow \sin \left( {9x - \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\)

\( \Leftrightarrow \sin \left( {9x - \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{6}\)

Bước 3:

\( \Leftrightarrow \left[ \begin{array}{l}9x - \dfrac{\pi }{3} = \dfrac{\pi }{6} + k2\pi \\9x - \dfrac{\pi }{3} = \pi  - \dfrac{\pi }{6} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{9}\\x = \dfrac{{7\pi }}{{54}} + \dfrac{{k2\pi }}{9}\end{array} \right.\)

Bước 4:

Vì \(x > 0\) nên \(\left[ \begin{array}{l}\dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{9} > 0 \Leftrightarrow k >  - \dfrac{1}{4} \Rightarrow {k_{\min }} = 0 \to x = \dfrac{\pi }{{18}}\\\dfrac{{7\pi }}{{54}} + \dfrac{{k2\pi }}{9} > 0 \Leftrightarrow k >  - \dfrac{7}{{12}} \Rightarrow {k_{\min }} = 0 \to x = \dfrac{{7\pi }}{{54}}\end{array} \right..\)

So sánh hai nghiệm ta được nghiệm dương nhỏ nhất là \(x = \dfrac{\pi }{{18}}.\)

Phương trình \( \Leftrightarrow \dfrac{1}{2}\sin 5x + \dfrac{{\sqrt 3 }}{2}\cos 5x = \sin 7x \) \(\Leftrightarrow \sin \left( {5x + \dfrac{\pi }{3}} \right) = \sin 7x\)

\( \Leftrightarrow \sin 7x = \sin \left( {5x + \dfrac{\pi }{3}} \right) \Leftrightarrow \left[ \begin{array}{l}7x = 5x + \dfrac{\pi }{3} + k2\pi \\7x = \pi  - \left( {5x + \dfrac{\pi }{3}} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = \dfrac{\pi }{{18}} + \dfrac{{k\pi }}{6}\end{array} \right.{\rm{ }}\left( {k \in \mathbb{Z}} \right).\)

+) $0 < \dfrac{\pi }{6} + k\pi  < \dfrac{\pi }{2}$$ \Leftrightarrow  - \dfrac{1}{6} < k < \dfrac{1}{3} \Rightarrow k = 0 \to x = \dfrac{\pi }{6}$

+) $0 < \dfrac{\pi }{{18}} + k\dfrac{\pi }{6} < \dfrac{\pi }{2}$$ \Leftrightarrow  - \dfrac{1}{3} < k < \dfrac{8}{3} \Rightarrow \left[ \begin{array}{l}k = 0 \to x = \dfrac{\pi }{{18}}\\k = 1 \to x = \dfrac{{2\pi }}{9}\\k = 2 \to x = \dfrac{{7\pi }}{{18}}\end{array} \right.$

Vậy có \(4\) nghiệm thỏa mãn..

Phương trình vô nghiệm $ \Leftrightarrow {1^2} + {1^2} < {\left[ {\sqrt 2 \left( {{m^2} + 1} \right)} \right]^2}$

$ \Leftrightarrow {m^4} + 2{m^2} > 0 \Leftrightarrow {m^2}\left( {{m^2} + 2} \right) > 0 \Leftrightarrow {m^2} > 0 \Leftrightarrow m \ne 0.$

Phương trình \( \Leftrightarrow \left( {m + 1} \right)\dfrac{{1 - \cos 2x}}{2} - \sin 2x + \cos 2x = 0\)

\( \Leftrightarrow  - 2\sin 2x + \left( {1 - m} \right)\cos 2x =  - m - 1.\)

Phương trình có nghiệm \( \Leftrightarrow {\left( { - 2} \right)^2} + {\left( {1 - m} \right)^2} \ge {\left( { - m - 1} \right)^2} \Leftrightarrow 4m \le 4 \Leftrightarrow m \le 1\)

\( \Rightarrow m \in \left\{ { - 2018; - 2017;...;0;1} \right\}\) nên có \(2020\) giá trị.

Phương trình \(2{\sin ^2}\dfrac{x}{4} - 3\cos \dfrac{x}{4} = 0 \Leftrightarrow 2\left( {1 - {{\cos }^2}\dfrac{x}{4}} \right) - 3\cos \dfrac{x}{4} = 0\)

\( \Leftrightarrow  - 2{\cos ^2}\dfrac{x}{4} - 3\cos \dfrac{x}{4} + 2 = 0 \) \(\Leftrightarrow \left[ \begin{array}{l}\cos \dfrac{x}{4} = \dfrac{1}{2}\\\cos \dfrac{x}{4} =  - 2\left( {L} \right)\end{array} \right. \) \(\Leftrightarrow \cos \dfrac{x}{4} = \dfrac{1}{2} \) \(\Leftrightarrow \cos \dfrac{x}{4} = \cos \dfrac{\pi }{3}\)

\( \Leftrightarrow \left[ \begin{array}{l}\dfrac{x}{4} = \dfrac{\pi }{3} + k2\pi \\\dfrac{x}{4} =  - \dfrac{\pi }{3} + k2\pi \end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{4\pi }}{3} + k8\pi \\x =  - \dfrac{{4\pi }}{3} + k8\pi \end{array} \right.\)

Với \(x = \dfrac{{4\pi }}{3} + k8\pi\). Ta tìm nghiệm của \(x\) trong \(\left[ {0;8\pi } \right]\). Khi đó: \( 0\le \dfrac{{4\pi }}{3} + k8\pi \le 8\pi \Leftrightarrow k=0 \Rightarrow x=\dfrac{4\pi}{3}\).

Với \(x =- \dfrac{{4\pi }}{3} + k8\pi\). Ta tìm nghiệm của \(x\) trong \(\left[ {0;8\pi } \right]\). Khi đó: \( 0\le -\dfrac{{4\pi }}{3} + k8\pi \le 8\pi \Leftrightarrow k=1 \Rightarrow x=\dfrac{20\pi}{3}\).

\( \to T = \dfrac{{4\pi }}{3} + \dfrac{{20\pi }}{3} = 8\pi \)

+) Nếu \(m = 0\) thì phương trình trở thành \(\tan x = 8\) có nghiệm nên \(m = 0\) thỏa mãn.

+) Nếu \(m \ne 0\) thì:

Điều kiện: \(\left\{ \begin{array}{l}\sin x \ne 0\\\cos x \ne 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\tan x \ne 0\\\cot x \ne 0\end{array} \right.\)

Phương trình $\tan x + m\cot x = 8$$ \Leftrightarrow \tan x + \dfrac{m}{{\tan x}} = 8$ $ \Leftrightarrow {\tan ^2}x - 8\tan x + m = 0\left( * \right)$

Để phương trình đã cho có nghiệm khi và chỉ khi \(\left( * \right)\) có nghiệm \(\tan x \ne 0\) $ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {\left( { - \,4} \right)^2} - m \ge 0\\{0^2} - 8.0 + m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 16\\m \ne 0\end{array} \right.$

Kết hợp hai trường hợp ta được \(m \le 16\)

Đặt \(t = \cos 3x{\rm{ }}\left( { - 1 \le t \le 1} \right)\).

Phương trình trở thành \(2{t^2} + \left( {3 - 2m} \right)t + m - 2 = 0.\)

Ta có \(\Delta  = {\left( {2m - 5} \right)^2}\). Suy ra phương trình có hai nghiệm \(\left[ \begin{array}{l}{t_1} = \dfrac{1}{2}\\{t_2} = m - 2\end{array} \right..\)

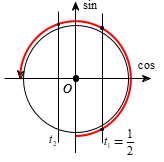
Ta thấy ứng với một nghiệm \({t_1} = \dfrac{1}{2}\) thì cho ta hai giá trị \(3x \in \left( { - \dfrac{\pi }{2};\pi } \right)\) hay có \(2\) nghiệm \(x\) thuộc khoảng \(\left( { - \dfrac{\pi }{6};\dfrac{\pi }{3}} \right).\)

Do đó yêu cầu bài toán thỏa nếu phương trình \(\cos 3x = m - 2\) chỉ có duy nhất \(1\) nghiệm thuộc \(\left( { - \dfrac{\pi }{6};\dfrac{\pi }{3}} \right)\)

Quan sát đường tròn đơn vị thì \(\left[ \begin{array}{l} - 1 < \cos 3x \le 0\\\cos 3x = 1\end{array} \right.\)  \( \Leftrightarrow \left[ \begin{array}{l} - 1 < {t_2} \le 0\\{t_2} = 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l} - 1 < m - 2 \le 0\\m - 2 = 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}1 < m \le 2\\m = 3\end{array} \right.\)

- Xét \(\cos x = 0\) thì phương trình trở thành \(1 = 0\) không thỏa mãn.

- Xét \(\cos x \ne 0\), chia cả hai vế của phương trình cho \({\cos ^2}x \ne 0\) và đặt \(\tan x = t\)

Phương trình \( \Leftrightarrow {\tan ^2}x - \left( {\sqrt 3  + 1} \right)\tan x + \sqrt 3 \; = 0 \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x = \sqrt 3 \end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = \dfrac{\pi }{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\)

Phương trình \( \Leftrightarrow {\sin ^2}x - 4\sin x\cos x + 4{\cos ^2}x = 5\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\)

\( \Leftrightarrow  - 4{\sin ^2}x - 4\sin x\cos x - {\cos ^2}x = 0 \Leftrightarrow {\left( {2\sin x + \cos x} \right)^2} = 0 \Leftrightarrow 2\sin x + \cos x = 0\)

\( \Leftrightarrow \tan x =  - \dfrac{1}{2}\) \( \Rightarrow \) có $2$ vị trí biểu diễn nghiệm trên đường tròn lượng giác.

Phương trình \( \Leftrightarrow 9{\sin ^2}x + \left( {m - 2} \right)\sin 2x + {\cos ^2}x = 0\)

\( \Leftrightarrow 9.\dfrac{{1 - \cos 2x}}{2} + \left( {m - 2} \right)\sin 2x + \dfrac{{1 + \cos 2x}}{2} = 0\)\( \Leftrightarrow \left( {m - 2} \right)\sin 2x - 4\cos 2x =  - 5\)

Phương trình có nghiệm \( \Leftrightarrow {\left( {m - 2} \right)^2} + 16 \ge 25 \Leftrightarrow {\left( {m - 2} \right)^2} \ge 9 \Leftrightarrow \left[ \begin{array}{l}m \ge 5\\m \le  - 1\end{array} \right.\)

\( \Rightarrow m \in \left\{ { - 10; - 9;...; - 1;5;6;...;10} \right\}\)$ \Rightarrow $  có \(16\) giá trị nguyên.

Phương trình \( \Leftrightarrow 2.\dfrac{{1 - \cos 2x}}{2} + m\sin 2x = 2m \Leftrightarrow m\sin 2x - \cos 2x = 2m - 1.\)

Phương trình vô nghiệm \( \Leftrightarrow {m^2} + 1 < {\left( {2m - 1} \right)^2} \Leftrightarrow 3{m^2} - 4m > 0 \Leftrightarrow \left[ \begin{array}{l}m < 0\\m > \dfrac{4}{3}\end{array} \right..\)

Đặt $t = \sin x + \cos x = \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right)$.

Vì $\sin \left( {x + \dfrac{\pi }{4}} \right) \in \left[ { - \,1;1} \right] \Rightarrow t \in \left[ { - \,\sqrt 2 ;\sqrt 2 } \right]$.

Ta có ${t^2} = {\left( {\sin x + \cos x} \right)^2} = {\sin ^2}x + {\cos ^2}x + 2\sin x\cos x \Rightarrow \sin x\cos x = \dfrac{{{t^2} - 1}}{2}$.

Khi đó, phương trình đã cho trở thành $\dfrac{{{t^2} - 1}}{2} + 2t = 2 \Leftrightarrow {t^2} + 4t - 5 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t =  - \,5\left( {L} \right)\end{array} \right..$

Với $t = 1$, ta được $\sin x + \cos x = 1 \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = \sin \dfrac{\pi }{4}$.

$ \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{4} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{4} = \pi  - \dfrac{\pi }{4} + k2\pi \end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.,\,\,k \in \mathbb{Z}$.

Đặt \(t = \sin x + \cos x\left( { - \sqrt 2  \le t \le \sqrt 2 } \right)\)\( \Rightarrow \sin x\cos x = \dfrac{{{t^2-1}}}{2}\)

Phương trình trở thành $\left( {1 + \sqrt 3 } \right)t - \left( {{t^2} - 1} \right) - \sqrt 3  - 1 = 0$

$ \Leftrightarrow {t^2} - \left( {1 + \sqrt 3 } \right)t + \sqrt 3  = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = \sqrt 3 \left( {L} \right)\end{array} \right. \Leftrightarrow t = 1.$

Đặt $t = \left| {\sin x + \cos x} \right| = \sqrt 2 \left| {\sin \left( {x + \dfrac{\pi }{4}} \right)} \right|$.

Vì $\sin \left( {x + \dfrac{\pi }{4}} \right) \in \left[ { - \,1;1} \right] \Rightarrow t \in \left[ {0;\sqrt 2 } \right]$.

Ta có ${t^2} = {\left( {\sin x + \cos x} \right)^2} = {\sin ^2}x + {\cos ^2}x + 2\sin x\cos x \Rightarrow \sin 2x = {t^2} - 1.$

Phương trình đã cho trở thành $2\left( {{t^2} - 1} \right) - 3\sqrt 6 \,t + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{{\sqrt 6 }}{2}\\t = \sqrt 6 \left( {L} \right)\end{array} \right.$

$\sin 2x = {t^2} - 1 = \dfrac{1}{2}.$

Đặt \(t = \sin x + \cos x{\rm{ }}\left( { - \sqrt 2  \le t \le \sqrt 2 } \right)\)\( \Rightarrow \sin x\cos x = \dfrac{{{t^2} - 1}}{2}\)

Phương trình trở thành \(\dfrac{{{t^2} - 1}}{2} - t + m = 0 \Leftrightarrow  - 2m = {t^2} - 2t - 1\)\( \Leftrightarrow {\left( {t - 1} \right)^2} =  - 2m + 2\)

Do \( - \sqrt 2  \le t \le \sqrt 2 \)\( \Rightarrow  - \sqrt 2  - 1 \le t - 1 \le \sqrt 2  - 1\) \( \Rightarrow 0 \le {\left( {t - 1} \right)^2} \le 3 + 2\sqrt 2 \)

Vậy để phương trình có nghiệm \( \Leftrightarrow 0 \le  - 2m + 2 \le 3 + 2\sqrt 2  \Leftrightarrow  - \dfrac{{1 + 2\sqrt 2 }}{2} \le m \le 1\)

\( \Rightarrow m \in \left\{ { - 1;0;1} \right\}.\)

Ta có: \( - 1 \le \sin x \le 1; - 1 \le \cos x \le 1\)

\(\begin{array}{l}{\sin ^3}x + {\sin ^2}x = {\sin ^2}x\left( {\sin x + 1} \right) \ge 0\\{\sin ^3}x - {\sin ^2}x = {\sin ^2}x\left( {\sin x - 1} \right) \le 0\end{array}\)

Do đó \( - {\sin ^2}x \le {\sin ^3}x \le {\sin ^2}x\)

Tương tự \( - {\cos ^2}x \le {\cos ^3}x \le {\cos ^2}x\)

\( \Rightarrow  - 2{\sin ^2}x - {\cos ^2}x \le y \le 2{\sin ^2}x + {\cos ^2}x\)

Mà \(\left\{ \begin{array}{l} - 2{\sin ^2}x - {\cos ^2}x =  - 1 - {\sin ^2}x \ge  - 1 - 1 =  - 2\\2{\sin ^2}x + {\cos ^2}x = 1 + {\sin ^2}x \le 1 + 1 = 2\end{array} \right.\)  nên \( - 2 \le y \le 2\)

Vậy \(M = 2\) đạt được khi \(\sin x = 1,\cos x = 0\)

 \(m =  - 2\) đạt được khi \(\sin x =  - 1,\cos x = 0\)

Do đó \({M^2} + {m^2} = 8\)