Tổng hợp câu hay và khó chương 5 - Phần 1

Bước 1: Tìm mối quan hệ giữa x và t

Khi A sang trái thì x tăng dần và y giảm dần

Tạo mối quan hệ giữa y và t

Vì xe A chuyển động đều với vận tốc là 2m/s nên mối quan hệ giữa x và t là: \(x = v.t = 2t\)

Bước 2: Tìm mối quan hệ giữa y và t

Mà ta có \(\sqrt {{x^2} + 144}  + \sqrt {{y^2} + 144}  = 39\) nên:

\(\sqrt {4{t^2} + 144}  + \sqrt {{y^2} + 144}  = 39\)

\( \Leftrightarrow \sqrt {{y^2} + 144}  = 39 - 2\sqrt {{t^2} + 36} \)

\( \Leftrightarrow {y^2} + 144\)\( = {39^2} + 4\left( {{t^2} + 36} \right)\)\( - 4.39\sqrt {{t^2} + 36} \)

\(\begin{array}{l} \Leftrightarrow {y^2} = 4{t^2} + {39^2} - 156\sqrt {{t^2} + 36} \\y = \sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} \end{array}\)

Quãng đường A đi được là 5m nên ta có t=2,5(s)

Bước 3: Tính quãng đường tại t=2,5(s)

Vận tốc tại thời điểm t=2,5 của B là \(y'\left( {2,5} \right)\). Khi đó

\(\begin{array}{l}y' = \dfrac{{\left( {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} \right)'}}{{2\sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\\ = \dfrac{{8t - 156.\dfrac{t}{{\sqrt {{t^2} + 36} }}}}{{2\sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\\ = \dfrac{{4t\left( {2 - 39.\dfrac{t}{{\sqrt {{t^2} + 36} }}} \right)}}{{2\sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\\ = \dfrac{{2t\left( {2\sqrt {{t^2} + 36}  - 39t} \right)}}{{\sqrt {{t^2} + 36} \sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\end{array}\)

Vậy \(y'\left( {2,5} \right) \approx  - 0,867\)

Vận tốc tức thời của xe B tại thời điểm xe A cách N 5m là -0,867(m/s).

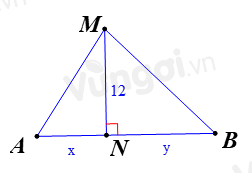
Bước 1: Xác định AM+BM, MN

Coi M, A, B là một tam giác và N thuộc cạnh AB

Sợi dây dài 39m => AM+BM=39

Có MN=12

Bước 2: Tìm mối liên hệ giữa x và y.

Theo định lý py-ta-go ta được:

\(\begin{array}{l}A{M^2} = A{N^2} + {12^2} = {x^2} + 144\\B{M^2} = B{N^2} + {12^2} = {y^2} + 144\\AM + BM = 39\\ \Leftrightarrow \sqrt {{x^2} + 144}  + \sqrt {{y^2} + 144}  = 39\end{array}\)

Vậy hệ thức cần tìm là \(\sqrt {{x^2} + 144}  + \sqrt {{y^2} + 144}  = 39\)

Ta có \(y' = 3{x^2} + 6x\).

Gọi \(A\left( {a;\,{a^3} + 3{a^2}} \right)\) thuộc đồ thị hàm số.

Phương trình tiếp tuyến $d$ của đồ thị hàm số tại \(A\) là \(y = \left( {3{a^2} + 6a} \right)\left( {x - a} \right) + {a^3} + 3{a^2}\).

$M\left( {m;\,0} \right) \in d$\( \Leftrightarrow \left( {3{a^2} + 6a} \right)\left( {m - a} \right) + {a^3} + 3{a^2} = 0\)\( \Leftrightarrow 2{a^3} - 3\left( {m - 1} \right){a^2} - 6ma = 0\) \( \Leftrightarrow \left[ \begin{array}{l}a = 0\\2{a^2} - 3\left( {m - 1} \right)a - 6m = 0\,\,\,\,\left( 1 \right)\end{array} \right.\).

Khi \(a = 0\) ta có phương trình tiếp tuyến \(y = 0\).

Đối với đồ thị hàm số không có tiếp tuyến nào vuông góc với \(y = 0\) nên yêu cầu bài toán tương đương phương trình \(\left( 1 \right)\) có hai nghiệm \({a_1}\) và \({a_2}\) khác \(0\) thỏa \(y'\left( {{a_1}} \right).y'\left( {{a_2}} \right) =  - 1\) $ \Leftrightarrow \left( {3a_1^2 + 6{a_1}} \right)\left( {3a_2^2 + 6{a_2}} \right) =  - 1$\( \Leftrightarrow 9{a_1}.{a_2}\left[ {{a_1}.{a_2} + 2\left( {{a_1} + {a_2}} \right) + 4} \right] + 1 = 0\) \( \Leftrightarrow 9\left( { - 3m} \right)\left[ { - 3m + 3\left( {m - 1} \right) + 4} \right] + 1 = 0\)\( \Leftrightarrow  - 27m + 1 = 0\)\( \Leftrightarrow m = \dfrac{1}{{27}}\).

Thay \(m = \dfrac{1}{{27}}\) vào \(\left( 1 \right)\) thử lại có 2 nghiệm phân biệt khác \(0\).

Từ \({\left[ {f\left( {2x + 1} \right)} \right]^2} + {\left[ {f\left( {1 - x} \right)} \right]^3} = x\) (*), cho \(x = 0\) ta có \({\left[ {f\left( 1 \right)} \right]^2} + {\left[ {f\left( 1 \right)} \right]^3} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}f\left( 1 \right) = 0\\f\left( 1 \right) =  - 1\end{array} \right.\)

Đạo hàm hai vế của (*) ta được \(4.f\left( {2x + 1} \right).f'\left( {2x + 1} \right) - 3{\left[ {f\left( {1 - x} \right)} \right]^2}.f'\left( {1 - x} \right) = 1\)

Cho \(x = 0\) ta được \(4f\left( 1 \right).f'\left( 1 \right) - 3.{\left[ {f\left( 1 \right)} \right]^2}.f'\left( 1 \right) = 1\)\( \Leftrightarrow f\left( 1 \right).f'\left( 1 \right).\left[ {4 - 3f\left( 1 \right)} \right] = 1\) (**)

Nếu \(f\left( 1 \right) = 0\) thì (**) vô lý, do đó \(f\left( 1 \right) =  - 1\), khi đó (**) trở thành

\( - f'\left( 1 \right).\left[ {4 + 3} \right] = 1\)\( \Leftrightarrow f'\left( 1 \right) =  - \dfrac{1}{7}\)

Phương trình tiếp tuyến \(y =  - \dfrac{1}{7}\left( {x - 1} \right) - 1\) \( \Leftrightarrow y =  - \dfrac{1}{7}x - \dfrac{6}{7}\)

Ta có \(y = \sin 3x.\cos x - \sin 2x\)\( = \dfrac{1}{2}\left( {\sin 4x + \sin 2x} \right) - \sin 2x\)\( = \dfrac{1}{2}\left( {\sin 4x - \sin 2x} \right)\)

Mặt khác theo quy nạp ta chứng minh được \({\left( {\sin ax} \right)^{\left( n \right)}} = {\left( { - 1} \right)^{n - 1}}{a^n}\sin \left( {\dfrac{{n\pi }}{2} - ax} \right)\)

Do đó \({y^{\left( {10} \right)}}\left( x \right) = \dfrac{1}{2}\left( {{{\left( { - 1} \right)}^9}{4^{10}}.\sin \left( {5\pi  - 4x} \right) - {{\left( { - 1} \right)}^9}{{.2}^{10}}.\sin \left( {5\pi  - 2x} \right)} \right)\)

\( = \dfrac{1}{2}\left( { - {4^{10}}.\sin 4x + {2^{10}}\sin 2x} \right)\)

\( \Rightarrow \) \({y^{\left( {10} \right)}}\left( {\dfrac{\pi }{3}} \right)\)\( \approx 454490.13\)

$y = \sqrt {1 + 3x - {x^2}} $$ \Rightarrow {y^2} = 1 + 3x - {x^2}$

$ \Rightarrow 2y.y' = 3 - 2x$$ \Rightarrow 2.{\left( {y'} \right)^2} + 2y.y'' =  - 2$$ \Rightarrow {\left( {y'} \right)^2} + y.y'' =  - 1$

+ Khi $0 < x < {x_0}$: $f\left( x \right) = a\sqrt x $ $ \Rightarrow f'\left( x \right) = \dfrac{a}{{2\sqrt x }}$.

Ta có $f'\left( x \right)$ xác định trên $\left( {0;{x_0}} \right)$ nên liên tục trên khoảng $\left( {0;{x_0}} \right)$.

+ Khi $x > {x_0}$: $f\left( x \right) = {x^2} + 12$ $ \Rightarrow f'\left( x \right) = 2x$. Ta có $f'\left( x \right)$ xác định trên $\left( {{x_0}; + \infty } \right)$ nên liên tục trên khoảng $\left( {{x_0}; + \infty } \right)$.

+ Tại $x = {x_0}$:

$\mathop {\lim }\limits_{x \to x_0^ - } \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to x_0^ - } \dfrac{{a\sqrt x  - a\sqrt {{x_0}} }}{{x - {x_0}}}$$ = \mathop {\lim }\limits_{x \to x_0^ - } \dfrac{{a\left( {\sqrt x  - \sqrt {{x_0}} } \right)}}{{x - {x_0}}}$$ = \mathop {\lim }\limits_{x \to x_0^ - } \dfrac{a}{{\sqrt x  + \sqrt {{x_0}} }}$$ = \dfrac{a}{{2\sqrt {{x_0}} }}$.

$\mathop {\lim }\limits_{x \to x_0^ + } \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to x_0^ + } \dfrac{{{x^2} + 12 - \left( {x_0^2 + 12} \right)}}{{x - {x_0}}}$$ = \mathop {\lim }\limits_{x \to x_0^ + } \dfrac{{{x^2} - x_0^2}}{{x - {x_0}}}$$ = \mathop {\lim }\limits_{x \to x_0^ + } \left( {x + {x_0}} \right)$$ = 2{x_0}$.

Hàm số $f$ có đạo hàm trên khoảng $\left( {0; + \infty } \right)$ khi và chỉ khi

$\mathop {\lim }\limits_{x \to x_0^ - } \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to x_0^ + } \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}$$ \Leftrightarrow \dfrac{a}{{2\sqrt {{x_0}} }} = 2{x_0}$.

Khi đó $f'\left( {{x_0}} \right) = \dfrac{a}{{2\sqrt {{x_0}} }} = 2{x_0}$ và $f'\left( x \right) = \left\{ \begin{array}{l}\dfrac{a}{{2\sqrt x }}{\rm{   khi }}0 < x < {x_0}\\2x{\rm{       khi }}x \ge {x_0}\end{array} \right.$ nên hàm số $f$ có đạo hàm liên tục trên khoảng $\left( {0; + \infty } \right)$.

Ta có $\dfrac{a}{{2\sqrt {{x_0}} }} = 2{x_0} \Leftrightarrow a = 4{x_0}\sqrt {{x_0}} $ $\left( 1 \right)$

Mặt khác: Hàm số $f$ liên tục tại ${x_0}$ nên $x_0^2 + 12 = a\sqrt {{x_0}} $ $\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra ${x_0} = 2$ và $a = 8\sqrt 2 $

Vậy $S = a + {x_0} = 2\left( {1 + 4\sqrt 2 } \right)$.

Ta có: \(y' = 3{x^2} + 6mx + m + 1\).

Hệ số góc của tiếp tuyến tại điểm có hoành độ \(x =  - 1\) là \(y'\left( { - 1} \right) = 4 - 5m\)

Khi \(x =  - 1\) thì \(y = 2m - 1\).

Phương trình tiếp tuyến của đồ thị hàm số tại điểm \(B\left( { - 1;2m - 1} \right)\) là:

\(y = y'\left( { - 1} \right)\left( {x + 1} \right) + y\left( 1 \right)\) hay \(y = \left( {4 - 5m} \right)\left( {x + 1} \right) + 2m - 1\)

Tiếp tuyến đi qua \(A\left( {1;3} \right)\) \( \Leftrightarrow 3 = \left( {4 - 5m} \right)\left( {1 + 1} \right) + 2m - 1 \Leftrightarrow m = \dfrac{1}{2}\)

Vậy \({m_0} = \dfrac{1}{2}\).

Ta có \(f\left( 0 \right) = 1\).

\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)\) \( = \mathop {\lim }\limits_{x \to {0^ + }} \left( {a{x^2} + bx + 1} \right)\) \( = 1\).

\(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\) \( = \mathop {\lim }\limits_{x \to {0^ - }} \left( {ax - b - 1} \right)\) \( =  - b - 1\).

Để hàm số có đạo hàm tại \({x_0} = 0\) thì hàm số phải liên tục tại \({x_0} = 0\) nên

\(f\left( 0 \right) = \mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\). Suy ra \( - b - 1 = 1\)\( \Leftrightarrow b =  - 2\).

Khi đó \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} - 2x + 1,x \ge 0\\ax + 1,x < 0\end{array} \right.\).

Xét:

+) \(\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{x}\) \( = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{a{x^2} - 2x + 1 - 1}}{x}\)\( = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax - 2} \right)\)\( =  - 2\).

+) \(\mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{x}\) \( = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{ax + 1 - 1}}{x}\)\( = \mathop {\lim }\limits_{x \to {0^ - }} \left( a \right)\) \( = a\).

Hàm số có đạo hàm tại \({x_0} = 0\)thì \(a =  - 2\).

Vậy với \(a =  - 2\),\(b =  - 2\) thì hàm số có đạo hàm tại \({x_0} = 0\) khi đó \(T =  - 6\).

Ta có \(y = {\sin ^2}x = \dfrac{{1 - {\rm{cos}}2x}}{2}\).

Khi đó \(y' = \sin 2x\) ; \(y'' = 2.c{\rm{os}}2x = 2.{\rm{sin}}\left( {2x + \dfrac{\pi }{2}} \right)\) ; \(y''' =  - {2^2}.{\rm{sin}}2x = {2^2}.{\rm{sin}}\left( {2x + \pi } \right)\)…

\({y^{\left( n \right)}} = {2^{n - 1}}\sin \left[ {2x + \dfrac{{\left( {n - 1} \right)\pi }}{2}} \right]\).

Vậy \({y^{\left( {2018} \right)}(\pi )} = {2^{2017}}.\sin \left( {2.\pi  + \dfrac{{2017\pi }}{2}} \right) \) \(= {2^{2017}}.\sin \left( {1010\pi  + \dfrac{\pi }{2}} \right) = {2^{2017}}\)

Đường thẳng $d$ đi qua điểm $A\left( {0;\,a} \right)$, hệ số góc $k$ có phương trình: $y = kx + a$.

Để $d$ là tiếp tuyến của $\left( C \right)$ thì hệ phương trình $\left\{ \begin{array}{l}\dfrac{{x + 2}}{{x - 1}} = kx + a{\rm{   }}\left( * \right)\\\dfrac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}} = k{\rm{         }}\left( {**} \right)\end{array} \right.$ có nghiệm.

Thay (**) vào (*) ta được: $\dfrac{{x + 2}}{{x - 1}} = \dfrac{{ - 3x}}{{{{\left( {x - 1} \right)}^2}}} + a$

$ \Leftrightarrow \left( {a - 1} \right){x^2} - 2\left( {a + 2} \right)x + a + 2 = 0$ với \(x \ne 1\). $\left( 1 \right)$

Do từ $A$ kẻ được hai tiếp tuyến đến $\left( C \right)$ nên phương trình $\left( 1 \right)$ có hai nghiệm phân biệt khác $1$.

$ \Leftrightarrow \left\{ \begin{array}{l}a \ne 1\\\Delta ' = 3\left( {a + 2} \right) > 0\\a - 1 - 2\left( {a + 2} \right) + a + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a >  - 2\\a \ne 1\end{array} \right.$. $\left( 2 \right)$

Khi đó toạ độ hai tiếp điểm là $M\left( {{x_1};\,\dfrac{{{x_1} + 2}}{{{x_1} - 1}}} \right)$ và $N\left( {{x_2};\,\dfrac{{{x_2} + 2}}{{{x_2} - 1}}} \right)$ với ${x_1}$, ${x_2}$ là nghiệm của $\left( 1 \right)$ do đó ${x_1} + {x_2} = \dfrac{{2\left( {a + 2} \right)}}{{a - 1}}$, ${x_1}{x_2} = \dfrac{{a + 2}}{{a - 1}}$.

Hai tiếp điểm nằm về hai phía của trục hoành khi

$\dfrac{{{x_1} + 2}}{{{x_1} - 1}}.\dfrac{{{x_2} + 2}}{{{x_2} - 1}} < 0$$ \Leftrightarrow \dfrac{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1}} < 0$ $ \Leftrightarrow \dfrac{{9a + 6}}{{ - 3}} < 0 \Leftrightarrow a >  - \dfrac{2}{3}$.

Kết hợp điều kiện $\left( 2 \right)$ suy ra $\left\{ \begin{array}{l}a >  - \dfrac{2}{3}\\a \ne 1\end{array} \right.$ nên trên đoạn $\left[ { - 2018;\,2018} \right]$ số giá trị nguyên của $a$ thỏa yêu cầu bài toán là $2018$.

\(y = \dfrac{{{x^2}}}{{x - 1}} = x + 1 + \dfrac{1}{{x - 1}}\)

Gọi điểm \(A\left( {a;2} \right) \in \left( d \right):y = 2\). Đường thẳng đi qua \(A\) có dạng \(y = k\left( {x - a} \right) + 2\)

Điều kiện tiếp xúc: \(\left\{ \begin{array}{l}\dfrac{{{x^2}}}{{x - 1}} = k\left( {x - a} \right) + 2\\\dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = k\end{array} \right.\)

Ta có: $\dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = k$ \(\Rightarrow \dfrac{{{{\left( {x - 1} \right)}^2} - 1}}{{{{\left( {x - 1} \right)}^2}}} = k\) \( \Rightarrow 1 - \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} = k\) \( \Rightarrow {\left( {x - 1} \right)^2} = \dfrac{1}{{1 - k}}\)

\(\dfrac{{{x^2}}}{{x - 1}} = k\left( {x - a} \right) + 2\)\( \Leftrightarrow x + 1 + \dfrac{1}{{x - 1}} = k\left( {x - a} \right) + 2\)  \( \Leftrightarrow x - 1 + \dfrac{1}{{x - 1}} = k\left( {x - 1} \right) + k\left( {1 - a} \right)\)

\( \Leftrightarrow {\left( {x - 1} \right)^2} + 1 = k{\left( {x - 1} \right)^2} + k\left( {1 - a} \right)\left( {x - 1} \right)\) \( \Leftrightarrow \left( {1 - k} \right){\left( {x - 1} \right)^2} + 1 = k\left( {1 - a} \right)\left( {x - 1} \right)\) \( \Leftrightarrow \left( {1 - k} \right).\dfrac{1}{{1 - k}} + 1 = k\left( {1 - a} \right)\left( {x - 1} \right)\) \( \Leftrightarrow 2 = k\left( {1 - a} \right)\left( {x - 1} \right)\) \( \Leftrightarrow x - 1 = \dfrac{2}{{k\left( {1 - a} \right)}}\)

\( \Rightarrow {\left[ {\dfrac{2}{{k\left( {1 - a} \right)}}} \right]^2} = \dfrac{1}{{1 - k}}\) \( \Leftrightarrow \dfrac{4}{{{k^2}{{\left( {1 - a} \right)}^2}}} = \dfrac{1}{{1 - k}}\) \( \Leftrightarrow {k^2}{\left( {1 - a} \right)^2} = 4\left( {1 - k} \right)\)

\( \Rightarrow \)\({\left( {1 - a} \right)^2}{k^2} + 4k - 4 = 0\)

Để \(2\) tiếp tuyến vuông góc nhau thì phương trình trên có hai nghiệm phân biệt \(k_1,k_2\) sao cho \(k_1.k_2=-1\)

\( \Rightarrow \) \(\dfrac{{ - 4}}{{{{\left( {1 - a} \right)}^2}}} =  - 1\)

\( \Rightarrow \)\(\left[ \begin{array}{l}a = 3\,\,\,\,\,\,\,\\a =  - 1\,\,\,\,\end{array} \right.\)

Vậy tổng hai hoành độ là \(2\).

TXĐ: $D = \mathbb{R}$.

\(y' = 6{x^2} - 12x\).

Hệ số góc của tiếp tuyến tại \({x_0}\) là \(k = y'\left( {{x_0}} \right)\).

\( \Leftrightarrow k = 6x_0^2 - 12{x_0}\)\( = 6\left( {x_0^2 - 2{x_0}} \right)\)\( = 6{\left( {{x_0} - 1} \right)^2} - 6 \ge  - 6\).

Hệ số góc nhỏ nhất bằng \( - 6\) khi \({x_0} = 1\)\( \Rightarrow {y_0} =  - 1\).

Phương trình tiếp tuyến là \(y =  - 6\left( {x - 1} \right) - 1\)\( \Leftrightarrow 6x + y - 5 = 0\).

Ta có \(y = {x^3} - 3{x^2} + 2\)$ \Rightarrow y' = 3{x^2} - 6x$.

Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm thuộc \(\left( C \right):y = {x^3} - 3{x^2} + 2\), suy ra tiếp tuyến của \(\left( C \right)\) tại \(M\) có phương trình là $y = \left( {3x_M^2 - 6{x_M}} \right)\left( {x - {x_M}} \right) + x_M^3 - 3x_M^2 + 2$.

Tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt \(\left( C \right)\) tại điểm \(N\left( {{x_N};{y_N}} \right)\) (khác \(M\)) nên \({x_M}\), \({x_N}\) là nghiệm của phương trình: ${x^3} - 3{x^2} + 2 = \left( {3x_M^2 - 6{x_M}} \right)\left( {x - {x_M}} \right) + x_M^3 - 3x_M^2 + 2$

$ \Leftrightarrow \left( {{x^3} - x_M^3} \right) - 3\left( {{x^2} - x_M^2} \right) - \left( {3x_M^2 - 6{x_M}} \right)\left( {x - {x_M}} \right) = 0$

$ \Leftrightarrow {\left( {x - {x_M}} \right)^2}\left( {x + 2{x_M} - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_M}\\x =  - 2{x_M} + 3\end{array} \right.$ \( \Rightarrow \,{x_N} =  - 2{x_M} + 3\).

Khi đó \(P = 5x_M^2 + x_N^2 = 5x_M^2 + {\left( { - 2{x_M} + 3} \right)^2} = 9x_M^2 - 12{x_M} + 9 \ge 9{\left( {{x_M} - \dfrac{2}{3}} \right)^2} + 5\)

Vậy \(P\) đạt giá trị nhỏ nhất bằng \(5\) khi \({x_M} = \dfrac{2}{3}\). Khi đó \(M\left( {\dfrac{2}{3};\dfrac{{26}}{{27}}} \right)\)\( \Rightarrow \,OM = \dfrac{{10\sqrt {10} }}{{27}}\).

Gọi $M\left( {{x_0};\sqrt {x_0^2 - 2{x_0} + 3} } \right)$ là tiếp điểm.

Phương trình tiếp tuyến của $\left( C \right)$ tại $M$ có dạng là $y - \sqrt {x_0^2 - 2{x_0} + 3}  = \dfrac{{{x_0} - 1}}{{\sqrt {x_0^2 - 2{x_0} + 3} }}\left( {x - {x_0}} \right)$$ \Leftrightarrow y = \dfrac{{{x_0} - 1}}{{\sqrt {x_0^2 - 2{x_0} + 3} }} \cdot x + \dfrac{{3 - {x_0}}}{{\sqrt {x_0^2 - 2{x_0} + 3} }}$.

Vì tiếp tuyến của $\left( C \right)$ tại $M$ đi qua điểm $A\left( {1;a} \right)$ nên ta có:

$a = \dfrac{{{x_0} - 1}}{{\sqrt {x_0^2 - 2{x_0} + 3} }} + \dfrac{{3 - {x_0}}}{{\sqrt {x_0^2 - 2{x_0} + 3} }} = \dfrac{2}{{\sqrt {x_0^2 - 2{x_0} + 3} }} \Leftrightarrow a\sqrt {x_0^2 - 2{x_0} + 3}  = 2$

$ \Leftrightarrow \left\{ \begin{array}{l}a > 0\\{a^2}\left( {x_0^2 - 2{x_0} + 3} \right) = 4\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}a > 0\\{a^2}x_0^2 - 2a^2{x_0} + 3{a^2} - 4 = 0\left(  *  \right)\end{array} \right.$.

Vì qua $A$ kẻ được đúng hai tiếp tuyến đến $\left( C \right)$ nên $\left(  *  \right)$ phải có hai nghiệm phân biệt

\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta ' =  - 2{a^4} + 4{a^2} > 0}\end{array}} \right.\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{0 < {a^2} < 2}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{ - \sqrt 2  < a < \sqrt 2 }\end{array}} \right. \Leftrightarrow 0 < a < \sqrt 2 \end{array}\)

Vì $a \in \mathbb{Z}$ nên $a = 1$.

Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(d\):

\({x^3} - 3x = k\left( {x + 1} \right) + 2\)\( \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x - 2 - k} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x =  - 1 \Rightarrow y = 2\\{x^2} - x - 2 - k = 0\left( 1 \right)\end{array} \right.\).

\(d\) cắt \(\left( C \right)\) tại ba điểm phân biệt \( \Leftrightarrow \)phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt khác \( - 1\)

\( \Leftrightarrow \left\{ \begin{array}{l}{\Delta _{\left( 1 \right)}} > 0\\g\left( { - 1} \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k >  - \dfrac{9}{4}\\k \ne 0\end{array} \right.\).

Khi đó, \(d\) cắt \(\left( C \right)\) tại \(M\left( { - 1;2} \right)\), \(N\left( {{x_1};{y_1}} \right)\), \(P\left( {{x_2};{y_2}} \right)\) với \({x_1},{x_2}\) là nghiệm của \(\left( 1 \right)\).

Theo định lý vietè: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = 1\\P = {x_1}{x_2} =  - k - 2\end{array} \right.\).

Tiếp tuyến tại \(N\) và \(P\) vuông góc với nhau \( \Leftrightarrow y'\left( {{x_1}} \right).y'\left( {{x_2}} \right) =  - 1\)\( \Leftrightarrow \left( {3x_1^2 - 3} \right)\left( {3x_2^2 - 3} \right) =  - 1\)

\( \Leftrightarrow 9x_1^2x_1^2 - 9\left( {x_1^2 + x_2^2} \right) + 9 =  - 1 \Leftrightarrow 9{P^2} + 18P - 9{S^2} + 9 =  - 1\)

\( \Leftrightarrow 9{k^2} + 18k + 1 = 0 \Leftrightarrow k = \dfrac{{ - 3 \pm 2\sqrt 3 }}{3}\).

Vậy tích các phần tử trong \(S\) là \(\dfrac{1}{9}\).

Gọi $d$ là đường thẳng qua $A\left( {m;\, - 10} \right)$ có hệ số góc $k$.

Suy ra $d:y = k\left( {x - m} \right) - 10$.

$d$ là tiếp tuyến của $\left( C \right)$khi hệ phương trình sau có nghiệm

$\left\{ \begin{array}{l}{x^3} - 3{x^2} - 9x + 10 = k\left( {x - m} \right) - 10\,\,\,\left( 1 \right)\\3{x^2} - 6x - 9 = k\end{array} \right.\,\,$

Thế $k$ vào (1), ta được $2{x^3} - \left( {3m + 3} \right){x^2} + 6mx + 9m - 20 = 0$ (*).

Để có đúng $2$ tiếp tuyến của $\left( C \right)$ qua $A$ thì phương trình (*) có 2 nghiệm.

Phương trình \(\left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \) \(\left( * \right)\) có thể đưa được về dạng \(2{\left( {x - a} \right)^2}\left( {x - b} \right) = 0\) với \(a \ne b\).

Ta có: $2{x^3} - \left( {3m + 3} \right){x^2} + 6mx + 9m - 20 = 2{\left( {x - a} \right)^2}\left( {x - b} \right)$

\( \Leftrightarrow 2{x^3} - \left( {3m + 3} \right){x^2} + 6mx + 9m - 20 = 2{x^3} - 2\left( {2a + b} \right){x^2} + 2\left( {{a^2} + 2ab} \right)x - 2{a^2}b\)

\( \Leftrightarrow \left\{ \begin{array}{l} - \left( {3m + 3} \right) =  - 2\left( {2a + b} \right)\,\,\left( 1 \right)\\6m = 2\left( {{a^2} + 2ab} \right)\,\,\,\left( 2 \right)\\9m - 20 =  - 2{a^2}b\,\,\left( 3 \right)\end{array} \right.\)

Từ \(\left( 2 \right) \Rightarrow 3m = {a^2} + 2ab = a\left( {a + 2b} \right)\) thay vào \(\left( 1 \right)\) được:

\( - \left( {{a^2} + 2ab} \right) - 3 =  - 4a - 2b\)\( \Leftrightarrow {a^2} - 4a + 3 + 2ab - 2b = 0\)

\( \Leftrightarrow \left( {a - 1} \right)\left( {a - 3} \right) + 2b\left( {a - 1} \right) = 0\)\( \Leftrightarrow \left( {a - 1} \right)\left( {a + 2b - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}a = 1\\a + 2b = 3\end{array} \right.\)

+) Với \(a = 1\) thì \(3m = 1 + 2b\) thay vào \(\left( 3 \right)\) ta được \(3\left( {1 + 2b} \right) - 20 =  - 2b \Leftrightarrow b = \dfrac{{17}}{8}\)

Suy ra \(m = \dfrac{{1 + 2b}}{3} = \dfrac{7}{4}\).

+) Với \(a + 2b = 3\) thì \(3m = 3a \Leftrightarrow m = a\) thay vào \(\left( 1 \right),\left( 3 \right)\) ta được:

\(\left\{ \begin{array}{l} - 3a - 3 =  - 4a - 2b\\9a - 20 =  - 2{a^2}b\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 3 - 2b\\9\left( {3 - 2b} \right) - 20 =  - 2{\left( {3 - 2b} \right)^2}.b\end{array} \right.\)  

\( \Leftrightarrow \left\{ \begin{array}{l}a = 3 - 2b\\8{b^3} - 24{b^2} + 7 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 3 - 2b\\b =  - \dfrac{1}{2},b = \dfrac{{7 \pm \sqrt {21} }}{4}\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}a = 4\\a = \dfrac{{ - 1 \pm \sqrt {21} }}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}m = 4\\m = \dfrac{{ - 1 \pm \sqrt {21} }}{2}\end{array} \right.\)

Vậy tập hợp các giá trị của \(m\) thỏa mãn là \(S = \left\{ {\dfrac{7}{4};4;\dfrac{{ - 1 \pm \sqrt {21} }}{2}} \right\}\).

Suy ra $T = \dfrac{7}{4} + \,4 + \,\dfrac{{ - 1 + \sqrt {21} }}{2} + \dfrac{{ - 1 - \sqrt {21} }}{2}$$ = \dfrac{{19}}{4}$.

Ta có: \(y' = 3{x^2} - 2mx - m\). Gọi \(M\left( {{x_0};\,{y_0}} \right) \in \left( C \right)\) suy ra hệ số góc của tiếp tuyến của \(\left( C \right)\) tại \(M\) có hệ số góc là \(k = y'\left( {{x_0}} \right) = 3x_0^2 - 2m{x_0} - m\)\( = 3{\left( {{x_0} - \dfrac{m}{3}} \right)^2} - \left( {\dfrac{{{m^2}}}{3} + m} \right)\)\( \ge  - \left( {\dfrac{{{m^2} + 3m}}{3}} \right)\).

Để mọi đường thẳng tiếp xúc với \(\left( C \right)\) đều có hệ số góc dương thì :

\( - \left( {\dfrac{{{m^2} + 3m}}{3}} \right) > 0\)\( \Leftrightarrow \left( {\dfrac{{{m^2} + 3m}}{3}} \right) < 0\)\( \Leftrightarrow  - 3 < m < 0\).

\( \Rightarrow \) Tập các giá trị nguyên của \(m\)là: \(T = \left\{ { - 2;\, - 1} \right\}\). Vậy tổng các phần tử của \(T\) là: \( - 3\).

Ta có \(y = {x^3} - 3x + 2\)\( \Rightarrow y' = 3{x^2} - 3\).

Gọi \({x_0}\) là hoành độ tiếp điểm, phương trình tiếp tuyến có dạng

$y = \left( {3x_0^2 - 3} \right)\left( {x - {x_0}} \right) + x_0^3 - 3{x_0} + 2$

Gọi \(M\left( {m;9m - 14} \right)\) là điểm nằm trên đường thẳng $d:y = 9x - 14$.

Tiếp tuyến đi qua điểm \(M\) khi và chỉ khi $9m - 14 = \left( {3x_0^2 - 3} \right)\left( {m - {x_0}} \right) + x_0^3 - 3{x_0} + 2\,\,\,\left( 1 \right)$

$ \Leftrightarrow \left( {{x_0} - 2} \right)\left[ {2x_0^2 - \left( {3m - 4} \right){x_0} + 8 - 6m} \right] = 0$ $ \Leftrightarrow \left( {{x_0} - 2} \right)\left[ {2x_0^2 - \left( {3m - 4} \right){x_0} + 8 - 6m} \right] = 0$

$ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\2x_0^2 - \left( {3m - 4} \right){x_0} + 8 - 6m = 0 = g\left( {{x_0}} \right)\,\,\,\,\,\left( 2 \right)\end{array} \right.$

Yêu cầu đề bài $ \Leftrightarrow $$\left( 2 \right)$ có hai nghiệm phân biệt có một nghiệm bằng $2$ hoặc $\left( 2 \right)$ có nghiệm kép khác $2$

$ \Leftrightarrow $$\left\{ \begin{array}{l}\Delta  > 0\\g\left( 2 \right) = 0\end{array} \right.$ hoặc $\left\{ \begin{array}{l}\Delta  = 0\\g\left( 2 \right) \ne 0\end{array} \right.$

$ \Leftrightarrow $$\left[ \begin{array}{l}\left\{ \begin{array}{l}9{m^2} + 24m - 48 > 0\\ - 12m + 24 = 0\end{array} \right.\\\left\{ \begin{array}{l}9{m^2} + 24m - 48 = 0\\ - 12m + 24 \ne 0\end{array} \right.\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = \dfrac{4}{3}\\m =  - 4\end{array} \right.$.

Vậy có $3$ điểm $M$ thỏa đề bài.

Vì hàm số đã cho là hàm số chẵn nên đồ thị $\left( C \right)$ của nó đối xứng qua $Oy$. Do đó từ điểm $A$ trên trục $Oy$ nếu kẻ được một tiếp tuyến $d$ đến $\left( C \right)$ thì ảnh của $d$ qua phép đối xứng trục $Oy$ cũng là một tiếp tuyến của $\left( C \right)$.

Vậy để qua điểm $A$ trên trục $Oy$ có thể kẻ đến $\left( C \right)$ đúng ba tiếp tuyến thì điều kiện cần và đủ là có một tiếp tuyến vuông góc với trục tung và một tiếp tuyến với nhánh phải của đồ thị $\left( C \right)$, tức là phần đồ thị của hàm số $y = f\left( x \right) = {x^3} - 3{x^2} + 1$, với $x \ge 0$.

Gọi $M\left( {0;m} \right)$ thuộc $Oy$ và $\left( \Delta  \right)$ là tiếp tuyến qua $M\left( {0;m} \right)$ có hệ số góc $k$. Ta có: $\left( \Delta  \right):y = kx + m$.

Điều kiện tiếp xúc là: $\left\{ \begin{array}{l}{x^3} - 3{x^2} + 1 = kx + m\\3{x^2} - 6x = k\end{array} \right.$

Suy ra: ${x^3} - 3{x^2} + 1 = x\left( {3{x^2} - 6x} \right) + m$$ \Leftrightarrow m =  - 2{x^3} + 3{x^2} + 1$  $\left( * \right)$

Yêu cầu đề bài tương đương phương trình $\left( * \right)$ có đúng một nghiệm $x = 0$ và một nghiệm $x > 0$.

Phương trình $\left( * \right)$ có nghiệm $x = 0$ nên $m = 1$.

Thử lại, với $m = 1$ thì $\left( * \right)$ trở thành: $ - 2{x^3} + 3{x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{3}{2}\end{array} \right.$ (đúng).

Vậy $m = 1$.