Câu hỏi:
2 năm trước
Đặt\(AN = x,\,0 < x \le 18\), và \(BN = y\), (đơn vị mét). Tìm một hệ thức liên hệ giữa \(x\) và \(y\).
Trả lời bởi giáo viên
Đáp án đúng: a
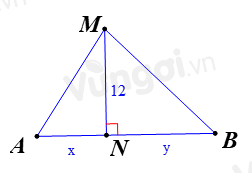
Bước 1: Xác định AM+BM, MN
Coi M, A, B là một tam giác và N thuộc cạnh AB
Sợi dây dài 39m => AM+BM=39
Có MN=12
Bước 2: Tìm mối liên hệ giữa x và y.
Theo định lý py-ta-go ta được:
\(\begin{array}{l}A{M^2} = A{N^2} + {12^2} = {x^2} + 144\\B{M^2} = B{N^2} + {12^2} = {y^2} + 144\\AM + BM = 39\\ \Leftrightarrow \sqrt {{x^2} + 144} + \sqrt {{y^2} + 144} = 39\end{array}\)
Vậy hệ thức cần tìm là \(\sqrt {{x^2} + 144} + \sqrt {{y^2} + 144} = 39\)
Hướng dẫn giải:
Coi M, A, B là một tam giác và N thuộc cạnh AB
Bước 1: Xác định AM+BM, MN
Bước 2: Tìm mối liên hệ giữa x và y.

