Cho hai hình bình hành \(ABCD,\,\,ABEF\) nằm trên hai mặt phẳng phân biệt. Gọi M,N lần lượt thuộc đoạn \(AC,\,\,BF\) sao cho \(\dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}}\)( Tham khảo hình vẽ). Đường thẳng \(MN\) song song với mặt phẳng nào sau đây?
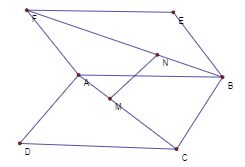
Bước 1:
Lấy \(H,\,\,K\) lần lượt trên \(AD,\,\,AF\) sao cho \(\dfrac{{AH}}{{AD}} = \dfrac{{AM}}{{AC}}\) và \(\dfrac{{AK}}{{FA}} = \dfrac{{BN}}{{BF}}\).
Bước 2:
Vì \(\dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}}\) nên \(\dfrac{{AH}}{{AD}} = \dfrac{{AK}}{{FA}}\)
Tam giác \(AFD\) có \(\dfrac{{AH}}{{AD}} = \dfrac{{AK}}{{FA}}\), áp dụng định lí Ta-lét đảo ta có \(HK\parallel DF\).
Tương tự ta có \(KN\parallel FE\)
Bước 3:
Do đó \(\left( {HKN} \right)\parallel \left( {DFE} \right) \Rightarrow \left( {MNKH} \right)\parallel \left( {DFEC} \right)\)\( \Rightarrow MN\parallel \left( {DCF} \right)\)
Cho hai mặt phẳng \(\left( \alpha \right);\,\,\left( \beta \right)\) song song với nhau. Xét hai đường thẳng \(a \subset \left( \alpha \right);\)\(b \subset \left( \beta \right)\). Tìm mệnh đề đúng trong các mệnh đề sau ?
Ta có \(a \subset \left( \alpha \right);\,\,b \subset \left( \beta \right)\) mà \(\left( \alpha \right)\parallel \left( \beta \right).\)
Do đó 2 đường thẳng a,b có thể song song hoặc chéo nhau.
Trong các mệnh đề sau, mệnh đề nào sai ?
Câu D sai vì hai đường thẳng phân biệt song song với cùng một mặt phẳng thì chúng song song hoặc chéo nhau.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB\), \(CD\), \(SA\) (Tham khảo hình vẽ). Có bao nhiêu khẳng định đúng trong các khẳng định sau:
i)\(\left( {MNP} \right)\parallel \left( {SBC} \right).\)
ii)\(NP\parallel \left( {SBC} \right).\)
iii)\(MP\parallel \left( {SCD} \right).\)
iv)\(MP\parallel \left( {SBC} \right).\)
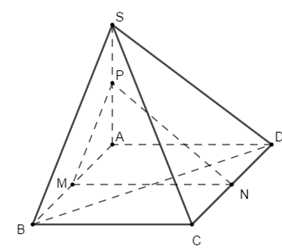
Bước 1:
Ta có \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,SA\).
Nên ta có \(\left\{ \begin{array}{l}MN\parallel BC\\MP\parallel SB\end{array} \right. \Rightarrow \left( {MNP} \right)\parallel \left( {SBC} \right)\)\( \Rightarrow \left\{ \begin{array}{l}NP\parallel \left( {SBC} \right)\\MP\parallel \left( {SBC} \right)\end{array} \right.\)
=>I;II;IV đúng.
Ta có \(MP\parallel SB\); SB cắt \(\left( {SCD} \right)\) tại S nên MP không song song với \(\left( {SCD} \right)\).
=> III sai.
Bước 2:
Vậy có 3 khẳng định đúng.
Chọn câu đúng :
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau nên A đúng.
Hai đường thẳng cùng song song với một mặt phẳng thì có thể cắt nhau, song song, trùng nhau hoặc chéo nhau nên B sai.
Hai mặt phẳng không cắt nhau thì song song hoặc trùng nhau nên C sai.
Hai mặt phẳng không song song thì trùng nhau hoặc cắt nhau nên D sai.
Cho một đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(\left( P \right)\)?
Nếu đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) thì có duy nhất một mặt phẳng chứa \(a\) và song song với \(\left( P \right)\).
Trong các mệnh đề sau, mệnh đề nào đúng?
Qua một điểm nằm ngoài một mặt phẳng cho trước có duy nhất một mặt phẳng song song với mặt phẳng đó.
Trong các điều kiện sau, điều kiện nào kết luận \(mp\left( \alpha \right)//mp\left( \beta \right)\)?
A sai vì \(\left( \alpha \right),\left( \beta \right)\) có thể trùng nhau.
B sai vì nếu a // b thì \(\left( \alpha \right),\left( \beta \right)\) chưa chắc song song với nhau.
C không thể kết luận được vị trí của \(\left( \alpha \right),\left( \beta \right)\).
D đúng vì dựa vào định nghĩa hai mặt phẳng song song khi mặt phẳng này chứa hai đường thẳng cắt nhau lần lượt song song với mặt phẳng kia.
Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau thì mọi đường thẳng nằm trong \(\left( \alpha \right)\) đều song song với \(\left( \beta \right)\).
Cho hai mặt phẳng song song \(\left( \alpha \right)\) và $\left( \beta \right)$, đường thẳng \(a//\left( \alpha \right)\) . Có mấy vị trí tương đối của $a$ với \(\left( \beta \right)\)?
Ta có: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( \beta \right)\\a//\left( \alpha \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}a \subset \left( \beta \right)\\a//\left( \beta \right)\end{array} \right.\)
Trong các mệnh đề sau, mệnh đề nào đúng?
A và B sai vì nếu \(\left( \alpha \right)//\left( \beta \right)\) và \(a \subset \left( \alpha \right),b \subset \left( \beta \right)\) thì a // b hoặc a và b chéo nhau.
C sai vì nếu a // b và \(a \subset \left( \alpha \right),b \subset \left( \beta \right)\) thì \(\left( \alpha \right)//\left( \beta \right)\) hoặc \(\left( \alpha \right) \cap \left( \beta \right) = c//a//b\)
D đúng.
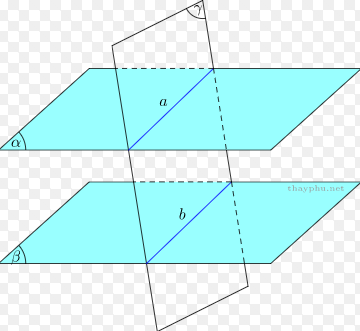
Hai đường thẳng $a$ và $b$ nằm trong \(mp\left( \alpha \right)\). Hai đường thẳng $a’$ và $b’$ nằm trong \(mp\left( \beta \right)\). Mệnh đề nào sau đây đúng?
Trong các đáp án đã cho chỉ có đáp án D đúng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
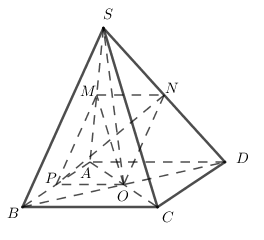
Dễ dàng chứng minh được $MNOP $ là hình bình hành \( \Rightarrow M,N,O,P\) đồng phẳng \( \Rightarrow A,C\) sai.
Ta có : $MN$ là đường trung bình của tam giác $SAD$ \( \Rightarrow MN//AD//BC\)
$ON$ là đường trung bình của tam giác $SBD$ \( \Rightarrow ON//SB\)
\( \Rightarrow (MON) // (SBC)\)
\( \Rightarrow \) Đáp án B đúng.
Đáp án D sai vì \(N \in \left( {MNP} \right) \cap \left( {SBD} \right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Thiết diện của (P) với hình chóp là hình gì ?
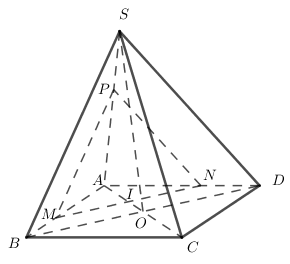
Trong $(ABCD)$ qua $I$ kẻ $MN // BD $ \(\left( {M \in AB;N \in AD} \right)\)
Trong $(SAB)$ qua $M$ kẻ $MP // SB$ \(\left( {P \in SA} \right)\)
\( \Rightarrow \left( {MNP} \right)//\left( {SBD} \right) \Rightarrow \left( P \right) \equiv \left( {MNP} \right)\)
\(\left\{ \begin{array}{l}\left( {MNP} \right) \cap \left( {SAD} \right) = NP\\\left( {SBD} \right) \cap \left( {SAD} \right) = SD\\\left( {MNP} \right)//\left( {SBD} \right)\end{array} \right. \Rightarrow NP//SD\)
Theo định lí Ta-let ta có: \(\dfrac{{MN}}{{BD}} = \dfrac{{AM}}{{AB}} = \dfrac{{AP}}{{AS}} = \dfrac{{MP}}{{SB}} = \dfrac{{NP}}{{SD}}\)
Mà tam giác \(SBD\) đều nên \(SB = BD = SD \Rightarrow MN = NP = MP\)
Vậy \(\Delta MNP\) đều.
Cho các mệnh đề sau:
1. Qua một điểm không thuộc hai mặt phẳng cắt nhau vẽ được duy nhất một đường thẳng song song với hai mặt đó.
2. Ba đường thẳng đôi một cắt nhau thì xác định một mặt phẳng.
3. Qua một điểm không thuộc hai đường thẳng chéo nhau vẽ được duy nhất một mặt phẳng song song với hai đường thẳng đó.
4. Ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song.
5. Nếu đường thẳng $d$ song song với đường thẳng $d’$ trong mặt phẳng $(P)$ thì đường thẳng $d$ song song hoặc nằm trong mặt phẳng $(P).$
6. Hai mặt phẳng cùng song song với một đường thẳng thì cắt nhau theo giao tuyến song song với đường thẳng đó.
Hãy chọn các mệnh đề đúng:
1. Qua một điểm vẽ đường thẳng song song với hai đường thẳng cắt nhau thì đường thẳng cần vẽ phải song song với giao tuyến của hai mặt phẳng đó. Qua một điểm không thuộc đường thẳng vẽ được duy nhất 1 đường thẳng song song với đường thẳng đã cho. Vậy 1. đúng.
2. Hai đường thẳng cắt nhau xác định một mặt phẳng. 2 sai
3. Giả sử a và b là hai đường thẳng chéo nhau, \(M \notin a,M \notin b\)
Qua M kẻ \(a'//a;\,\,b'//b \Rightarrow a',b'\) là duy nhất.
\(a' \cap b' = \left\{ M \right\} \Rightarrow \) mặt phẳng (P) xác định bới a’, b’ là duy nhất. Và ta có : \(\left( P \right)//a,\,\,\left( P \right)//b\). Vậy 3 đúng.
4, 5. Hiển nhiên đúng.
6. Hai mặt phẳng cùng song song với một đường thẳng thì có thể song song hoặc trùng nhau, hoặc cắt nhau theo giao tuyến song song với đường thẳng đó. Vậy 6 sai.
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
Ta có \(AD \cap \left( {BEF} \right) = A \Rightarrow A\) sai.
Ta có: \(\left\{ \begin{array}{l}AF//BE\\AD//BC\end{array} \right. \Rightarrow \left( {AFD} \right)//\left( {BEC} \right) \Rightarrow \) B đúng.
\(\left( {ABD} \right) \cap \left( {EFC} \right) = CD \Rightarrow C\) sai.
\(EC \cap \left( {ABF} \right) = E \Rightarrow D\)sai.
Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Mặt phẳng \(\left( \alpha \right)\) cắt $SA, SB, SC, SD$ theo thứ tự lần lượt tại $A’, B’, C’, D’$ (không đồng thời trùng với các đầu mút). \(A'B'C'D'\) là hình bình hành khi và chỉ khi:
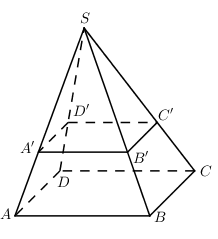
Do $A',B',C',D'$ không đồng thời trùng với các đầu mút nên loại đáp án C.
Gọi $a$ là đường thẳng qua $S$ và song song với $AB, b$ là đường thẳng qua $S$ và song song với $AD.$
$A’B’C’D’$ là hình bình hành khi và chỉ khi \(\left\{ \begin{array}{l}A'B'//C'D'\\A'B' = C'D'\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}a = \left( {SAB} \right) \cap \left( {SCD} \right)\\A'B'//C'D'\\A'B' \subset \left( {SAB} \right),\,\,C'D' \subset \left( {SCD} \right)\end{array} \right. \Rightarrow A'B'//a\)
Suy ra $A’B’ // AB$ $(1)$
Tương tự ta có: \(\left\{ \begin{array}{l}b = \left( {SAD} \right) \cap \left( {SBC} \right)\\A'D'//B'C'\\A'D' \subset \left( {SAD} \right),\,\,C'B' \subset \left( {SBC} \right)\end{array} \right. \Rightarrow A'D'//b\)
Suy ra $A’D’ // AD$ $(2)$
Từ $(1)$ và $(2)$ \( \Rightarrow \left( {A'B'C'D'} \right)//\left( {ABCD} \right)\) hay \(\left( \alpha \right)//\left( {ABCD} \right)\)
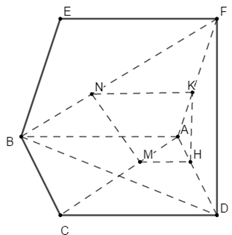
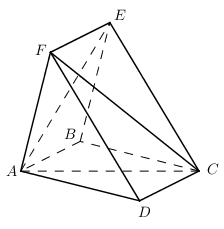
Cho hai hình vuông $ABCD,ABEF$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo $AC$ và $BF$ ta lấy các điểm $M, N$ sao cho $AM = BN.$ Mặt phẳng $(P)$ chứa $MN$ và song song với $AB$ cắt $AD$ và $AF$ lần lượt tại $M’, N’.$ Khẳng định nào sau đây là đúng?
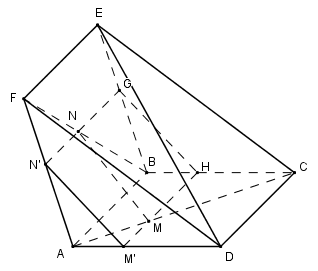
Trong (ABCD) qua M kẻ MM’ // AB \(\left( {M' \in AD} \right)\)
Trong (ABEF) qua N kẻ NN’ // AB \(\left( {N' \in AF} \right)\)
Ta có:
\(\left\{ \begin{array}{l}\dfrac{{AM'}}{{AD}} = \dfrac{{AM}}{{AC}}\\\dfrac{{AN'}}{{AF}} = \dfrac{{BN}}{{BF}}\\AM = BN;AC = BF\end{array} \right. \Rightarrow \dfrac{{AM'}}{{AD}} = \dfrac{{AN'}}{{AF}} \Rightarrow M'N'//DF\)
Lại có NN’ // AB // EF \( \Rightarrow \left( {MM'N'N} \right)//\left( {DEF} \right)\)
Mà \(MN \subset \left( {MM'N'N} \right) \Rightarrow MN//\left( {DEF} \right)\)
Cho hình chóp $S.ABC $ có đáy là tam giác $ABC$ thỏa mãn $AB = AC = 4,$ \(\widehat {BAC} = {30^0}\) . Mặt phẳng $(P)$ song song với $(ABC)$ cắt đoạn $SA$ tại $M$ sao cho $SM = 2MA.$ Diện tích thiết diện của $(P)$ và hình chóp $S.ABC$ bằng bao nhiêu?
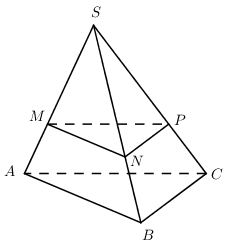
Trong (SAB) qua M kẻ MN // AB, trong (SAC) kẻ MP // AC. Khi đó ta có (MNP) // (ABC).
\( \Rightarrow \left( {MNP} \right) \equiv \left( P \right)\).
Thiết diện của (P) và hình chóp là tam giác MNP đồng dạng với tam giác ABC theo tỉ số \(\dfrac{{MN}}{{AB}} = \dfrac{{SM}}{{SA}} = \dfrac{2}{3}\)
\( \Rightarrow \dfrac{{{S_{MNP}}}}{{{S_{ABC}}}} = {\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9} \Rightarrow {S_{MNP}} = \dfrac{4}{9}{S_{ABC}}\)
Ta có ${S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC} = \dfrac{1}{2}.4.4.\sin {30^0} = 4$
\( \Rightarrow {S_{MNP}} = \dfrac{4}{9}.4 = \dfrac{{16}}{9}\)
Cho hình chóp S.ABCD có đáy ABCD là hình thang có các đáy AD và BC. Gọi M là trọng tâm tam giác SAD, N là điểm thuộc AC sao cho \(NA = \dfrac{{NC}}{2}\), P là điểm thuộc đoạn CD sao cho \(PD = \dfrac{{PC}}{2}\) . Khi đó mệnh đề nào sau đây là đúng?
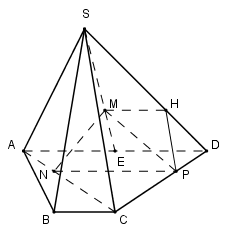
Gọi \(H \in SD\) sao cho \(HD = \dfrac{1}{2}SH\)
Ta có: \(\dfrac{{SM}}{{SE}} = \dfrac{{SH}}{{SD}} = \dfrac{2}{3} \Rightarrow MH//AD//NP \Rightarrow M,H,P,N\) đồng phẳng.
Ta có:
\(\begin{array}{l}\dfrac{{AN}}{{AC}} = \dfrac{{DP}}{{DC}} = \dfrac{1}{3} \Rightarrow NP//AD;\,\,\dfrac{{DH}}{{DS}} = \dfrac{{DP}}{{DC}} = \dfrac{1}{3} \Rightarrow HP//SC\\\left\{ \begin{array}{l}NP//AD//BC\\HP//SC\end{array} \right. \Rightarrow \left( {MHPN} \right)//\left( {SBC} \right) \Rightarrow \left( {MNP} \right)//\left( {SBC} \right)\\MN \subset \left( {MNP} \right) \Rightarrow MN//\left( {SBC} \right)\end{array}\)

