Câu hỏi:
2 năm trước
Cho hình chóp $S.ABC $ có đáy là tam giác $ABC$ thỏa mãn $AB = AC = 4,$ \(\widehat {BAC} = {30^0}\) . Mặt phẳng $(P)$ song song với $(ABC)$ cắt đoạn $SA$ tại $M$ sao cho $SM = 2MA.$ Diện tích thiết diện của $(P)$ và hình chóp $S.ABC$ bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: a
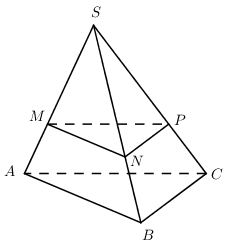
Trong (SAB) qua M kẻ MN // AB, trong (SAC) kẻ MP // AC. Khi đó ta có (MNP) // (ABC).
\( \Rightarrow \left( {MNP} \right) \equiv \left( P \right)\).
Thiết diện của (P) và hình chóp là tam giác MNP đồng dạng với tam giác ABC theo tỉ số \(\dfrac{{MN}}{{AB}} = \dfrac{{SM}}{{SA}} = \dfrac{2}{3}\)
\( \Rightarrow \dfrac{{{S_{MNP}}}}{{{S_{ABC}}}} = {\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9} \Rightarrow {S_{MNP}} = \dfrac{4}{9}{S_{ABC}}\)
Ta có ${S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC} = \dfrac{1}{2}.4.4.\sin {30^0} = 4$
\( \Rightarrow {S_{MNP}} = \dfrac{4}{9}.4 = \dfrac{{16}}{9}\)
Hướng dẫn giải:
Qua M kẻ các đường thẳng song song với AB và AC. Xác định mặt phẳng (P) và thiết diện của (P) với hình chóp là tam giác MNP.
Chứng minh thiết diện là tam giác đồng dạng với tam giác ABC theo tỉ số k nào đó \( \Rightarrow \dfrac{{{S_{MNP}}}}{{{S_{ABC}}}} = {k^2}\) .
Tính diện tích tam giác ABC từ đó suy ra diện tích tam giác MNP.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
