Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB\), \(CD\), \(SA\) (Tham khảo hình vẽ). Có bao nhiêu khẳng định đúng trong các khẳng định sau:
i)\(\left( {MNP} \right)\parallel \left( {SBC} \right).\)
ii)\(NP\parallel \left( {SBC} \right).\)
iii)\(MP\parallel \left( {SCD} \right).\)
iv)\(MP\parallel \left( {SBC} \right).\)
Trả lời bởi giáo viên
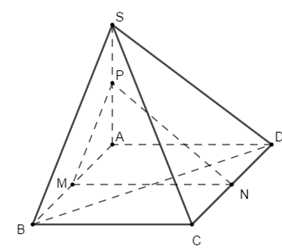
Bước 1:
Ta có \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,SA\).
Nên ta có \(\left\{ \begin{array}{l}MN\parallel BC\\MP\parallel SB\end{array} \right. \Rightarrow \left( {MNP} \right)\parallel \left( {SBC} \right)\)\( \Rightarrow \left\{ \begin{array}{l}NP\parallel \left( {SBC} \right)\\MP\parallel \left( {SBC} \right)\end{array} \right.\)
=>I;II;IV đúng.
Ta có \(MP\parallel SB\); SB cắt \(\left( {SCD} \right)\) tại S nên MP không song song với \(\left( {SCD} \right)\).
=> III sai.
Bước 2:
Vậy có 3 khẳng định đúng.
Hướng dẫn giải:
Bước 1: Kiểm tra từng đáp án
Dựa vào tính chất song song để chứng minh.
Bước 2: Kết luận