Câu hỏi:
2 năm trước
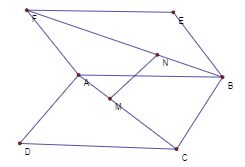
Cho hai hình bình hành \(ABCD,\,\,ABEF\) nằm trên hai mặt phẳng phân biệt. Gọi M,N lần lượt thuộc đoạn \(AC,\,\,BF\) sao cho \(\dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}}\)( Tham khảo hình vẽ). Đường thẳng \(MN\) song song với mặt phẳng nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: b
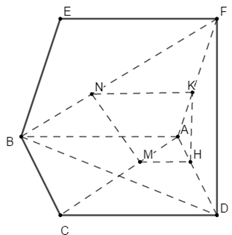
Bước 1:
Lấy \(H,\,\,K\) lần lượt trên \(AD,\,\,AF\) sao cho \(\dfrac{{AH}}{{AD}} = \dfrac{{AM}}{{AC}}\) và \(\dfrac{{AK}}{{FA}} = \dfrac{{BN}}{{BF}}\).
Bước 2:
Vì \(\dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}}\) nên \(\dfrac{{AH}}{{AD}} = \dfrac{{AK}}{{FA}}\)
Tam giác \(AFD\) có \(\dfrac{{AH}}{{AD}} = \dfrac{{AK}}{{FA}}\), áp dụng định lí Ta-lét đảo ta có \(HK\parallel DF\).
Tương tự ta có \(KN\parallel FE\)
Bước 3:
Do đó \(\left( {HKN} \right)\parallel \left( {DFE} \right) \Rightarrow \left( {MNKH} \right)\parallel \left( {DFEC} \right)\)\( \Rightarrow MN\parallel \left( {DCF} \right)\)
Hướng dẫn giải:
Bước 1: Lấy \(H,\,\,K\) lần lượt trên \(AD,\,\,AF\) sao cho \(\dfrac{{AH}}{{AD}} = \dfrac{{AM}}{{AC}}\) và \(\dfrac{{AK}}{{FA}} = \dfrac{{BN}}{{BF}}\).
Bước 2: Chứng minh \(HK\parallel DF\) và \(KN\parallel FE\)
Bước 3: Chứng minh hai mặt phẳng song song rồi suy ra tính chất song song của đường thẳng và mặt phẳng.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
