Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SD. Gọi P, Q, R lần lượt là trung điểm của AB, ON, SB. Chọn mệnh đề sai trong các mệnh đề sau:
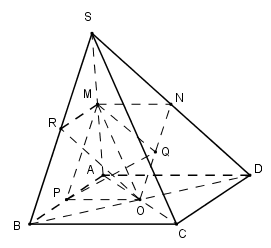
\(\left\{ \begin{array}{l}MR//AB//CD\\OR//SD\end{array} \right. \Rightarrow \left( {MOR} \right)//\left( {SCD} \right) \Rightarrow B\) đúng.
\(\left\{ \begin{array}{l}MN//AD//BC\\ON//SB\end{array} \right. \Rightarrow \left( {MON} \right)//\left( {SBC} \right) \Rightarrow C\) đúng.
Ta có:
\(\left\{ \begin{array}{l}MP//SB\\OP//BC\end{array} \right. \Rightarrow \left( {MNOP} \right)//\left( {SBC} \right);\,\,PQ \subset \left( {MNOP} \right) \Rightarrow PQ//\left( {SBC} \right)\) \( \Rightarrow D\) đúng.
Vậy A sai.
Cho tứ diện $ABCD,$ gọi \({G_1};{G_2};{G_3}\) lần lượt là trọng tâm các tam giác $ABC, ACD, ADB.$ Diện tích thiết diện tạo bởi mặt phẳng \(\left( {{G_1}{G_2}{G_3}} \right)\) bằng $k$ lần diện tích tam giác $BCD,$ khi đó $k$ bằng

Gọi $M, N, P$ lần lượt là trung điểm của $BC, CD, BD.$ Ta có:
\(\begin{array}{l}\dfrac{{A{G_1}}}{{AM}} = \dfrac{{A{G_2}}}{{AN}} = \dfrac{{A{G_3}}}{{AP}} = \dfrac{2}{3}\\ \Rightarrow {G_1}{G_2}//MN,\,\,{G_2}{G_3}//NP \Rightarrow \left( {{G_1}{G_2}{G_2}} \right)//\left( {MNP} \right)\end{array}\)
Qua \({G_1}\) kẻ \(B'C'//BC\,\,\left( {B' \in AB,C' \in AC} \right)\)
Qua \({G_2}\) kẻ \(C'D'//DC\,\,\left( {D' \in AD} \right)\)
Khi đó thiết diện của hình chóp cắt bởi \(\left( {{G_1}{G_2}{G_3}} \right)\) là \(\Delta B'C'D'\)
Ta có: \(\dfrac{{B'C'}}{{BC}} = \dfrac{{A{G_1}}}{{AM}} = \dfrac{2}{3} \Rightarrow \Delta B'C'D'\) đồng dạng với \(\Delta BCD\) theo tỉ số \(\dfrac{2}{3}\).
\( \Rightarrow \dfrac{{{S_{\Delta B'C'D'}}}}{{{S_{\Delta BCD}}}} = {\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}\).
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$ và có $AC = a, BD = b. $ Tam giác $SBD$ là tam giác đều. Một mặt phẳng $(P)$ di động song song với $(SBD)$ đi qua $I$ trên đoạn $OC.$ Đặt \(AI = x\,\,\left( {\dfrac{a}{2} < x < a} \right)\). Khi đó diện tích thiết diện của hình chóp với mặt phẳng $(P)$ là:
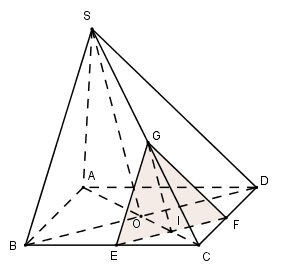
Trong $(ABCD)$ qua $I$ kẻ $EF // BD$ \(\left( {E \in BC;F \in CD} \right)\)
Trong $(SAC)$ qua $I$ kẻ $IG // SO$ \(\left( {G \in SC} \right)\)
\( \Rightarrow \left( {GEF} \right)\) qua $I$ và song song với $(SBD)$ \( \Rightarrow \left( P \right) \equiv \left( {GEF} \right)\)
Ta có: \(\left\{ \begin{array}{l}\left( {GEF} \right) \cap \left( {SBC} \right) = GE\\\left( {SBD} \right) \cap \left( {SBC} \right) = SB\\\left( {GEF} \right)//\left( {SBD} \right)\end{array} \right. \Rightarrow GE//SB\)
Tương tự ta chứng minh được $GF // SD.$
Ta có:
\(\left\{ \begin{array}{l}\dfrac{{IC}}{{OC}} = \dfrac{{FE}}{{BD}} = \dfrac{{GC}}{{SC}} = \dfrac{{GE}}{{SB}} = \dfrac{{GF}}{{SD}}\\BD = SB = SD\end{array} \right. \Rightarrow GE = GF = EF \Rightarrow \Delta GEF\) đều và \(\dfrac{{IC}}{{OC}} = \dfrac{{EF}}{{BD}}\) \( \Rightarrow EF = \dfrac{{IC}}{{OC}}.BD = \dfrac{{a - x}}{{\frac{a}{2}}}.b = \dfrac{{2b\left( {a - x} \right)}}{a}\)
\( \Rightarrow \Delta GEF\) đều cạnh \(\dfrac{{2(a - x)}}{a}.b\) , do đó \({S_{\Delta GEF}} = \dfrac{{{{\left( {\dfrac{{2(a - x)}}{a}} \right)}^2}.{b^2}\sqrt 3 }}{2} = \dfrac{{{b^2}{{\left( {a - x} \right)}^2}\sqrt 3 }}{{{a^2}}}\)
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB = 3a, AD = CD = a. Mặt bên (SAB) là tam giác cân tại S, SA = 2a. Mặt bên \(\left( \alpha \right)\) di động và song song với (SAB) đồng thời cắt các cạnh AD, BC, SC, SD theo thứ tự M, N, P, Q. Biết tứ giác MNPQ ngoại tiếp một đường tròn bán kính r. Tính r?
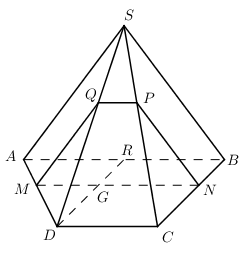
Lấy điểm \(M \in AD,\) trong (ABCD) qua M kẻ MN // AB \(\left( {N \in BC} \right)\). Trong (SAD) qua M kẻ MQ // SA, trong (SBC) qua N kẻ NP // SB.
\( \Rightarrow \left( {MNPQ} \right)//\left( {SAB} \right)\) .
Ta có: \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {ABCD} \right) = MN\\\left( {MNPQ} \right) \cap \left( {SCD} \right) = PQ\\\left( {ABCD} \right) \cap \left( {SCD} \right) = CD\end{array} \right. \Rightarrow MN//PQ//CD \Rightarrow \) MNPQ là hình thang.
Lại có \(\left\{ \begin{array}{l}\widehat {QMN} = \widehat {\left( {MN;MQ} \right)} = \widehat {\left( {AB;AS} \right)} = \widehat {SAB}\\\widehat {PNM} = \widehat {\left( {NM;NP} \right)} = \widehat {\left( {BA;BS} \right)} = \widehat {SBA}\end{array} \right. \Rightarrow \widehat {QMN} = \widehat {PNM}\)
Do đó MNPQ là hình thang cân.
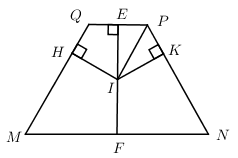
Giả sử MNPQ ngoại tiếp được đường tròn tâm I, gọi E và F lần lượt là trung điểm của PQ và MN.
Do MNPQ là hình thang cân nên \(I \in EF\).
Kẻ $IH \bot MQ;\,\,IK \bot NP$.
Ta có: \(IE = IF = IH = IK\), xét tam giác vuông IPE và IPK có IC chung, IE = IK \( \Rightarrow \Delta IPE = \Delta IPK\,\,\left( {ch - cgv} \right) \Rightarrow EP = KP\)
Chứng minh tương tự ta có: \(QE = QH,\,\,NK = NF,\,\,MH = MF\)
\( \Rightarrow MN + PQ = MQ + NP = 2MQ\,\,\,\left( * \right)\)
Đặt AM = x (0 < x < a). Theo định lí Ta-let ta có: \(\dfrac{{DM}}{{DA}} = \dfrac{{MQ}}{{SA}} \Rightarrow MQ = \dfrac{{DM.SA}}{{DA}} = \dfrac{{\left( {a - x} \right).2a}}{a} = 2\left( {a - x} \right)\)
Ta có : \(\dfrac{{PQ}}{{CD}} = \dfrac{{SQ}}{{SD}} = \dfrac{{AM}}{{AD}} \Rightarrow \dfrac{{PQ}}{a} = \dfrac{x}{a} \Rightarrow PQ = x\) .
Kẻ DR // BC, gọi \(G = DR \cap MN\) , dễ thấy RB = GN = CD = a.
\(\dfrac{{MG}}{{AR}} = \dfrac{{DM}}{{DA}} \Rightarrow MG = \dfrac{{AR.DM}}{{DA}} = \dfrac{{2a.\left( {a - x} \right)}}{a} = 2\left( {a - x} \right) \Rightarrow MN = MG + GN = 3a - 2x\)
Thay vào (*) ta có : \(3a - 2x + x = 4\left( {a - x} \right) \Leftrightarrow 3a - x = 4a - 4x \Leftrightarrow 3x = a \Leftrightarrow x = \dfrac{a}{3}\).
\( \Rightarrow MN = \dfrac{{7a}}{3},\,\,MQ = \dfrac{{4a}}{3};\,\,PQ = \dfrac{a}{3}\)
Ta có : \(EF = \sqrt {M{Q^2} - {{\left( {\dfrac{{MN - PQ}}{2}} \right)}^2}} = \dfrac{{a\sqrt 7 }}{3} \Rightarrow r = \dfrac{1}{2}EF = \dfrac{{a\sqrt 7 }}{6}.\)

