Câu hỏi:
2 năm trước
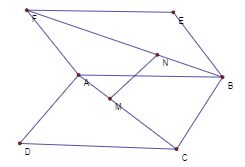
Cho tứ diện $ABCD,$ gọi \({G_1};{G_2};{G_3}\) lần lượt là trọng tâm các tam giác $ABC, ACD, ADB.$ Diện tích thiết diện tạo bởi mặt phẳng \(\left( {{G_1}{G_2}{G_3}} \right)\) bằng $k$ lần diện tích tam giác $BCD,$ khi đó $k$ bằng
Trả lời bởi giáo viên
Đáp án đúng: a
Gọi $M, N, P$ lần lượt là trung điểm của $BC, CD, BD.$ Ta có:
\(\begin{array}{l}\dfrac{{A{G_1}}}{{AM}} = \dfrac{{A{G_2}}}{{AN}} = \dfrac{{A{G_3}}}{{AP}} = \dfrac{2}{3}\\ \Rightarrow {G_1}{G_2}//MN,\,\,{G_2}{G_3}//NP \Rightarrow \left( {{G_1}{G_2}{G_2}} \right)//\left( {MNP} \right)\end{array}\)
Qua \({G_1}\) kẻ \(B'C'//BC\,\,\left( {B' \in AB,C' \in AC} \right)\)
Qua \({G_2}\) kẻ \(C'D'//DC\,\,\left( {D' \in AD} \right)\)
Khi đó thiết diện của hình chóp cắt bởi \(\left( {{G_1}{G_2}{G_3}} \right)\) là \(\Delta B'C'D'\)
Ta có: \(\dfrac{{B'C'}}{{BC}} = \dfrac{{A{G_1}}}{{AM}} = \dfrac{2}{3} \Rightarrow \Delta B'C'D'\) đồng dạng với \(\Delta BCD\) theo tỉ số \(\dfrac{2}{3}\).
\( \Rightarrow \dfrac{{{S_{\Delta B'C'D'}}}}{{{S_{\Delta BCD}}}} = {\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}\).
Hướng dẫn giải:
+) Chứng minh \(\left( {{G_1}{G_2}{G_2}} \right)//\left( {MNP} \right) \Rightarrow \) Cách dựng thiết diện.
+) Chứng minh thiết diện vừa dựng được là tam giác đồng dạng với tam giác $BCD.$
+) Sử dụng tính chất: Tỉ số diện tích bằng bình phương tỉ số đồng dạng.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
