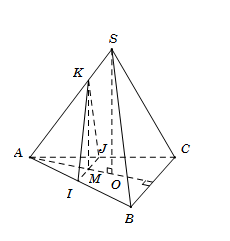
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, \(SA \bot \left( {ABC} \right)\),$SA = a$. Gọi $\left( P \right)$ là mặt phẳng đi qua $S$ và vuông góc với $BC$. Thiết diện của $\left( P \right)$ và hình chóp $S.ABC$ có diện tích bằng ?

Kẻ \(AE \bot BC,SA \bot BC \Rightarrow BC \bot \left( {SAE} \right) \equiv \left( P \right)\)
Thiết diện của mặt phẳng \(\left( P \right)\) và hình chóp \(S.ABC\) là tam giác \(SAE\) có diện tích ${S_{SAE}} = \dfrac{1}{2}SA.AE = \dfrac{1}{2}a.a.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4}$
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), cạnh bên \(SA \bot \left( {ABC} \right).\) Mặt phẳng \(\left( P \right)\) đi qua trung điểm \(M\) của \(AB\) và vuông góc với $SB$ cắt \(AC,SC,SB\) lần lượt tại \(N,P,Q.\) Tứ giác \(MNPQ\) là hình gì ?
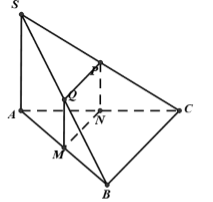
Ta có: \(\left\{ \begin{array}{l}AB \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot SB.\)
Vậy \(\left\{ \begin{array}{l}BC \bot SB\\\left( P \right) \bot SB\end{array} \right. \Rightarrow \left( P \right)//BC\left( 1 \right).\)
Mà \(\left( P \right) \cap \left( {ABC} \right) = MN\left( 2 \right).\)
Từ \(\left( 1 \right);\left( 2 \right) \Rightarrow MN//BC\)
Tương tự ta có \(PQ//BC\) nên MN//PQ hay thiết diện là hình thang.
\(\left\{ \begin{array}{l}
BC \bot \left( {SAB} \right)\\
MN//BC
\end{array} \right. \) \(\Rightarrow MN \bot \left( {SAB} \right) \Rightarrow MN\bot MQ\)
Vậy thiết diện là hình thang \(MNPQ\) vuông tại \(M\) và \(Q\).
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều, \(SA \bot \left( {ABC} \right)\). Gọi $\left( P \right)$ là mặt phẳng qua $B$ và vuông góc với $SC$. Thiết diện của $\left( P \right)$ và hình chóp $S.ABC$ là:

Gọi \(I\) là trung điểm của \(AC\), kẻ \(IH \bot SC\).
Ta có \(BI \bot AC,\,BI \bot SA \Rightarrow BI \bot SC\).
Do đó \(SC \bot \left( {BIH} \right)\) hay thiết diện là tam giác \(BIH\).
Mà \(BI \bot \left( {SAC} \right)\) nên \(BI \bot IH\) hay thiết diện là tam giác vuông.
Tam giác $ABC$ có$BC = 2a$, đường cao \(AD = a\sqrt 2 \). Trên đường thẳng vuông góc với $\left( {ABC} \right)$ tại $A$, lấy điểm $S$ sao cho \(SA = a\sqrt 2 \). Gọi $E,F$ lần lượt là trung điểm của $SB$ và$SC$. Diện tích tam giác $AEF$ bằng?

Do\(AD \bot BC,SA \bot BC \Rightarrow BC \bot \left( {SAD} \right)\)\( \Rightarrow BC \bot AH \Rightarrow EF \bot AH\)
\( \Rightarrow {S_{\Delta AEF}} = \dfrac{1}{2}EF.AH\)
Mà \(EF = \dfrac{1}{2}BC = a\). Do \(H\) là trung điểm \(SD \Rightarrow AH = \dfrac{1}{2}SD = a\) \( \Rightarrow {S_{\Delta AEF}} = \dfrac{1}{2}{a^2}\)
Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt đáy, \(ABCD\) là hình vuông cạnh \(a\sqrt 2 \), \(SA = 2a\). Gọi \(M\) là trung điểm cạnh \(SC\), \(\left( \alpha \right)\) là mặt phẳng đi qua \(A\), \(M\) và song song với đường thẳng \(BD\). Tính diện tích thiết diện của hình chóp bị cắt bởi mặt phẳng \(\left( \alpha \right)\).

Gọi \(O = AC \cap BD\), \(I = SO \cap AM\). Trong mặt phẳng \(\left( {SBD} \right)\) qua \(I\) kẻ \(EF//BD\), khi đó ta có \(\left( {AEMF} \right) \equiv \left( \alpha \right)\) là mặt phẳng chứa \(AM\) và song song với \(BD\). Do đó thiết diện của hình chóp bị cắt bởi mặt phẳng \(\left( \alpha \right)\) là tứ giác \(AEMF\)
Ta có: $\left\{ {\begin{array}{*{20}{l}}{FE\,{\rm{//}}\,BD}\\{BD \bot \left( {SAC} \right)}\end{array}} \right.$$ \Rightarrow FE \bot \left( {SAC} \right)$$ \Rightarrow FE \bot AM$.
Mặt khác ta có:
*\(AC = 2a = SA\) nên tam giác \(SAC\) vuông cân tại \(A\), suy ra \(AM = a\sqrt 2 \).
* \(I\) là trọng tâm tam giác \(SAC\), mà \(EF\,{\rm{//}}\,BD\) nên tính được \(EF = \dfrac{2}{3}BD = \dfrac{{4a}}{3}\).
Tứ giác \(AEMF\) có hai đường chéo \(FE \bot AM\) nên \({S_{AEMF}} = \dfrac{1}{2}FE.AM = \dfrac{{2{a^2}\sqrt 2 }}{3}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(AB = 8a\), \(SA = SB = SC = SD = 8a\). Gọi \(N\) là trung điểm cạnh \(SD\). Tính diện tích thiết diện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \(\left( {ABN} \right)\).

Mặt phẳng \(\left( {ABN} \right)\) chứa \(AB{\rm{//}}CD\) nên cắt mặt phẳng \(\left( {SCD} \right)\) theo giao tuyến \(NM{\rm{//}}CD\) và \(M\) cũng là trung điểm của \(SC\). Suy ra thiết diện cần tìm là hình thang cân \(ABMN\).
Hạ \(NI \bot AB\). Ta có \(N{I^2} = A{N^2} - A{I^2}\) với \(AN = \dfrac{{8a\sqrt 3 }}{2} = 4a\sqrt 3 \).
\(2AI = AB - MN\)\( = 8a - 4a = 4a \Rightarrow AI = 2a\). Từ đó suy ra \(NI = 2a\sqrt {11} \).
Vậy \({S_{ABMN}} = \dfrac{1}{2}\left( {AB + MN} \right).NI\)\( = \dfrac{1}{2}\left( {8a + 4a} \right)2a\sqrt {11} = 12{a^2}\sqrt {11} \).
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(2a\),\(SA = 2a\sqrt[{}]{3}\). Gọi \(I\) là trung điểm của \(AD\), mặt phẳng \(\left( P \right)\) qua \(I\) và vuông góc với \(SD\). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\).
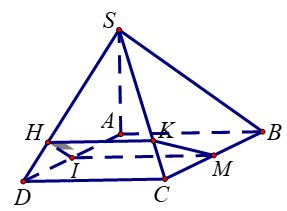
Kẻ \(IM{\rm{//}}CD\) với \(M \in BC\).
Ta có \(\left. \begin{array}{l}IM \bot SA\\IM \bot AD\end{array} \right\}\)\( \Rightarrow IM \bot \left( {SAD} \right)\)\( \Rightarrow IM \bot SD\)\( \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = IM\).
Kẻ \(IH \bot SD\) với \(H \in SD\)\( \Rightarrow \left( P \right) \cap \left( {SAD} \right) = IH\).
Vì \(\left. \begin{array}{l}IM{\rm{//}}CD\\IM \subset \left( P \right)\\CD \subset \left( {SCD} \right)\end{array} \right\}\)\( \Rightarrow \left( P \right) \cap \left( {SCD} \right) = HK\) với \(HK{\rm{//}}IM\left( {{\rm{//}}CD} \right)\)và \(K \in SC\).
\(\left( P \right) \cap \left( {SBC} \right) = KM\).
Vì \(IM \bot \left( {SAD} \right)\) nên \(IM \bot IH\). Do đó thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\) là hình thang \(IHKM\) vuông tại \(I\)và \(H\).
Ta có \(IM = AB = 2a\).
Xét \(\Delta SAD\) có: \(\tan \widehat {SAD} = \dfrac{{SA}}{{AD}}\)\( = \dfrac{{2\sqrt[{}]{3}a}}{{2a}}\)\( = \sqrt[{}]{3}\)\( \Rightarrow \widehat {SDA} = 60^\circ \).
Xét \(\Delta DHI\) có: \(\sin \widehat {HDI} = \dfrac{{HI}}{{ID}}\)\( \Rightarrow HI = ID.\sin 60^\circ \)\( = a.\dfrac{{\sqrt[{}]{3}}}{2}\).
Xét \(\Delta SAD\) có: \(SD = \sqrt[{}]{{S{A^2} + A{D^2}}}\)\( = \sqrt[{}]{{12{a^2} + 4{a^2}}}\)\( = 4a\).
Xét \(\Delta DHI\) có: \(HD = \sqrt[{}]{{I{D^2} - I{H^2}}}\)\( = \sqrt[{}]{{{a^2} - \dfrac{{3{a^2}}}{4}}}\)\( = \dfrac{a}{2}\)\( \Rightarrow SH = SD - HD\)\( = 4a - \dfrac{a}{2}\)\( = \dfrac{{7a}}{2}\).
Vì \(HK{\rm{//}}CD\) nên theo Talet ta có \(\dfrac{{HK}}{{CD}} = \dfrac{{SH}}{{SD}}\)\( = \dfrac{{\dfrac{{7a}}{2}}}{{4a}} = \dfrac{7}{8}\)\( \Rightarrow HK = \dfrac{7}{8}CD\)\( = \dfrac{7}{8}.2a\)\( = \dfrac{{7a}}{4}\).
Do đó diện tích thiết diện là \({S_{IHKM}} = \dfrac{{\left( {IM + HK} \right).IH}}{2}\)\( = \dfrac{{\left( {2a + \dfrac{{7a}}{4}} \right).\dfrac{{a\sqrt[{}]{3}}}{2}}}{2}\)\( = \dfrac{{15\sqrt[{}]{3}{a^2}}}{{16}}\).
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a,\,\,\,SA \bot \left( {ABC} \right),\,\,\,SA = \dfrac{{a\sqrt 3 }}{2}.$ Gọi $\left( P \right)$ là mặt phẳng đi qua $A$ và vuông góc với \(BC.\) Thiết diện của hình chóp $S.ABC$ được cắt bởi $\left( P \right)$ có diện tích bằng ?
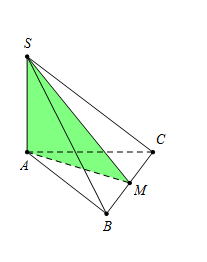
Gọi $M$ là trung điểm của $BC$ thì $BC \bot AM\,\,\,\,\,\,\,\,\,\left( 1 \right).$
Hiển nhiên \(AM = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
Mà $SA \bot \left( {ABC} \right) \Rightarrow BC \bot SA\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).$
Từ \(\left( 1 \right)\,\)và \(\left( 2 \right)\) suy ra \(BC \bot \left( {SAM} \right) \Rightarrow \left( P \right) \equiv \left( {SAM} \right).\)
$ \Rightarrow $ Thiết diện của hình chóp $S.ABC$ được cắt bởi $(P)$ chính là \(\Delta SAM.\)
Và \(\Delta \,SAM\) vuông tại $A$ nên \({S_{\Delta SAM}} = \dfrac{1}{2}SA.AM \) \(= \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}.a\sqrt 3 = \dfrac{{3{a^2}}}{4}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với $mp\,\,\left( {ABCD} \right).$ Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ và vuông góc với $SB.$ Mặt phẳng $\left( \alpha \right)$ cắt hình chóp theo thiết diện là hình gì ?
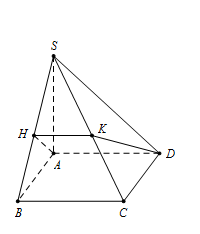
Ta có $AD$ vuông góc với $SA$ và $ AB$ $ \Rightarrow AD \bot mp\,\,\left( {SAB} \right) \Rightarrow AD \bot SB.$
Vẽ đường cao $AH$ trong tam giác $SAB$
Lại có $AD$ và $AH$ qua $A$ và vuông góc với $SB.$
Vậy mặt phẳng $\left( \alpha \right)$ chính là mặt phẳng $(AHD).$
Mặt khác $AD // mp(SBC) $ mà $AD \subset mp\,\,\left( {AHD} \right)$
Vậy mặt phẳng $(SBC)$ cắt mặt phẳng $(AHD) $ theo giao tuyến $HK // AD.$
Do đó mặt cắt là hình thang $ADKH $ mà $AD \bot mp\,\,\left( {SAB} \right)$$ \Rightarrow \,AD \bot AH.$
Vậy $ADKH $ là hình thang vuông.
Cho tứ diện đều $ABCD$ cạnh $a = 12,$ gọi $\left( P \right)$ là mặt phẳng qua $B$ và vuông góc với $AD.$ Thiết diện của $\left( P \right)$ và hình chóp có diện tích bằng

Gọi $E $ là trung điểm của $AD$ ta có \(BE \bot AD,CE \bot AD \Rightarrow AD \bot \left( {BCE} \right) \Rightarrow \left( P \right) \equiv \left( {BCD} \right)\)
Thiết diện là tam giác $BCE.$
Gọi $F$ là trung điểm của $BC.$
Ta có \(BE = CE = \dfrac{{12\sqrt 3 }}{2} = 6\sqrt 3 ;\) \(EF = \sqrt {B{E^2} - B{F^2}} = 6\sqrt 2 \)
Diện tích thiết diện là \(S = \dfrac{1}{2}EF.BC = \dfrac{1}{2}.6\sqrt 2 .12 = 36\sqrt 2 \)
Cho tứ diện đều $ABCD$ cạnh $a = 12$, $AP$ là đường cao của tam giác$ACD$. Mặt phẳng $\left( P \right)$ qua $B$ vuông góc với $AP$ cắt mp$\left( {ACD} \right)$ theo đoạn giao tuyến có độ dài bằng ?
Gọi \(G\) là trọng tâm tam giác \(ACD\) thì \(BG \bot \left( {ACD} \right)\) (tính chất tứ diện đều)
Kẻ \(KL\) đi qua trọng tâm \(G\) của \(\Delta ACD\) và song song với \(CD\) \( \Rightarrow AP \bot KL\) \( \Rightarrow \left( P \right)\) chính là mặt phẳng \(\left( {BKL} \right)\) \( \Rightarrow \left( {ACD} \right) \cap \left( {BKL} \right) = KL = \dfrac{2}{3}CD = 8\)

Cho tam giác cân $ABC,$ $AB = AC = a\sqrt 5 $ $BC = 4a.$ Trên nửa đường thẳng vuông góc với mặt phẳng chứa tam giác $ABC$ tại $A$ lấy một điểm $D$ sao cho $AD = a\sqrt 3 .$ Người ta cắt hình chóp bằng một mặt phẳng $\left( P \right)$ vuông góc với đường cao $AH$ của tam giác $ABC.$ Thiết diện là hình gì ?
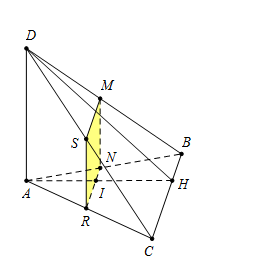
Ta có $AH$ vuông góc với $BC$ và $AD.$
Vậy $(P)$ là mặt phẳng song song với $BC$ và $AD.$
Lại có $BC // (P)$ nên $(P)$ cắt hai mặt phẳng $(ABC)$ và $(DBC)$ theo hai giao tuyến $NR$ và $MS$ với $NR // MS // BC.$
Mà $AD // (P)$ nên $\left( P \right)$ cắt hai mặt phẳng $(ACD)$ và $(BAD)$ theo hai giao tuyến $RS$ và $NM$ với $RS // MN // AD.$
Mặt khác $NM // AD$ và $AD \bot NR$\( \Rightarrow MN \bot NR\) suy ra $MNRS$ là hình chữ nhật.
Cho lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều, chiều cao bằng \(\dfrac{1}{2}\) cạnh đáy. Thiết diện của hình lăng trụ và mặt phẳng qua $B'$ vuông góc với $A'C$ là
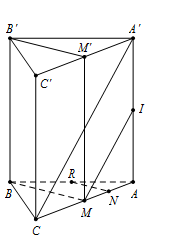
Gọi $M, M’, N, R$ lần lượt là trung điểm của $AC, A’C’, AM$ và $AB.$
Tam giác $A’B’C’$ đều suy ra $B'M' \bot A'C'.$
Mà $AA’$ vuông góc với đáy $(A’B’C’)$ $ \Rightarrow \,\,AA' \bot B'M'.$
Vậy $B’M’$ vuông góc với $(ACC’A’)$ $ \Rightarrow $$B'M' \bot A'C.$
Gọi $I$ là trung điểm của $AA’,$ ta có $A’C // MI.$
Mà $M’A’AM $ là hình vuông $ \Rightarrow \,\,M'N \bot MI.$
Do đó $M'N \bot A'C.$
Suy ra mặt cắt là $mp\,\,\left( {B'M'N} \right)$.
Mặt phẳng này cắt hai mặt phẳng song song $\left( {ABC} \right)$ và $\left( {A'B'C'} \right)$ theo hai giao tuyến $B’M’$ và $NR$ song song nhau.
Mặt khác $B'M' \bot \left( {ACC'A'} \right) \Rightarrow B'M' \bot M'N.$
Vậy $B’M’NR$ là hình thang vuông.
Cho tứ diện $SABC$ có hai tam giác $\Delta ABC$ và $\Delta SBC$ là hai tam giác đều cạnh $a,\,\,\,SA = \dfrac{{a\sqrt 3 }}{2}.$ Gọi $M$ là điểm trên $AB$ sao cho $AM = b{\rm{ }}\left( {0 < b < a} \right).$ $\left( P \right)$ là mặt phẳng qua $M$ và vuông góc với $BC.$ Thiết diện của $\left( P \right)$ và tứ diện $SABC$ có diện tích bằng ?
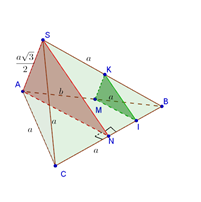
Gọi $N$ là trung điểm của $BC.$
Ta có \(\left\{ \begin{array}{l}SB = SC\\AB = AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}BC \bot SN\\BC \bot AN\end{array} \right. \Rightarrow BC \bot \left( {SAN} \right).\)
Theo bài ra \(BC \bot \left( P \right) \Rightarrow \left\{ \begin{array}{l}M \in \left( P \right)\\\left( P \right)//\left( {SAN} \right)\end{array} \right.\).
Kẻ \(MI//AN,\,MK//SA\)
\( \Rightarrow \) Thiết diện của $\left( P \right)$ và $S.ABC$ là \(\Delta KMI\)
Mà \(\left\{ \begin{array}{l}\Delta ABC\\\Delta SBC\end{array} \right.\) là hai tam giác đều cạnh $a$
$\Rightarrow AN = SN = \dfrac{{a\sqrt 3 }}{2} = SA $ $\Rightarrow \Delta SAN$ là tam giác đều cạnh \(\dfrac{{a\sqrt 3 }}{2}\)
\(\Rightarrow \Delta KMI\) là tam giác đều cạnh \(\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a - b}}{a}= \frac{{\sqrt 3 }}{2}\left( {a - b} \right)\)
\(\Rightarrow {S_{\Delta KMI}} = \dfrac{{3\sqrt 3 }}{{16}}(a-b)^2\)
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều, $O$ là trung điểm của đường cao $AH$ của tam giác $ABC,{\rm{ }}SO$ vuông góc với đáy. Gọi $I$ là điểm tùy ý trên $OH$ (không trùng với $O$ và $H$). mặt phẳng $\left( P \right)$ qua $I$ và vuông góc với $OH$. Thiết diện của $\left( P \right)$ và hình chóp $S.ABC$ là hình gì?

Mặt phẳng $(P)$ vuông góc với $OH$ nên $(P)$ song song với $SO.$
Suy ra $(P)$ cắt $(SAH)$ theo giao tuyến là đường thẳng qua $I$ và song song với $SO$ cắt $SH$ tại $K.$
Từ giả thiết suy ra $(P)$ song song $BC,$ do đó \((P)\) sẽ cắt $(ABC), (SBC)$ lần lượt là các đường thẳng qua $I$ và $K$ song song với $BC$ cắt $AB, AC.$ $SB, SC$ lần lượt tại $M, N, P, Q. $
Do đó thiết diện là tứ giác $MNPQ.$
Ta có $MN$ và $PQ$ cùng song song \(BC \Rightarrow I\) là trung điểm của $MN$ và $K$ là trung điểm của $PQ.$
Mà $IK // SO $ nên \(IK \bot MN,IK \bot PQ\)
Do đó $MNPQ$ là hình thang cân.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$ và $SA = SB = SC = b$ (\(a > b\sqrt 2 \)). Gọi $G$ là trọng tâm$\Delta \,ABC$. Xét mặt phẳng $\left( P \right)$ đi qua $A$ và vuông góc với $SC$ tại điểm I nằm giữa $S$ và $C$. Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( P \right)$ là
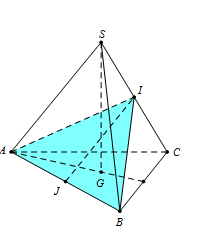
Kẻ \(AI \bot SC\), ta dễ dàng chứng minh được \(\Delta SAI = \Delta SBI\,\,\left( {c.g.c} \right) \Rightarrow \widehat {SIA} = \widehat {SIB} = {90^0} \Rightarrow BI \bot SC\)
\( \Rightarrow SC \bot \left( {ABI} \right)\). Thiết diện là tam giác $AIB.$
Ta có $AI = AC\sin \widehat {ACS} = a.\sqrt {1 - {{\cos }^2}\widehat {ACS}} = a.\sqrt {1 - \left( {\dfrac{{{a^2} + {b^2} - {b^2}}}{{2ab}}} \right)} = a\sqrt {1 - \dfrac{a}{{2b}}} .$
Gọi $J$ là trung điểm của $AB.$ Dễ thấy tam giác $AIB$ cân tại $I,$ suy ra \(IJ \bot AB\)
$ \Rightarrow IJ = \sqrt {A{I^2} - A{J^2}} = \sqrt {{a^2}\left( {1 - \dfrac{a}{{2b}}} \right) - \dfrac{{{a^2}}}{4}} = a\sqrt {\dfrac{3}{4} - \dfrac{a}{{2b}}} = \dfrac{a}{{2b}}\sqrt {3{b^2} - 2ab} $
Do đó: \(S = \dfrac{1}{2}AB.IJ = \dfrac{{{a^2}\sqrt {3{b^2} - 2ab} }}{{4b}}\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với $mp\,\,\left( {ABCD} \right),\,\,SA = a\sqrt 2 .$ Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ và vuông góc với $SB.$ Mặt phẳng $\left( \alpha \right)$ cắt hình chóp theo một thiết diện có diện tích $S.$ Tính $S$ theo $a.$
Ta có AD vuông góc với SA và AB$ \Rightarrow AD \bot mp\,\,\left( {SAB} \right) \Rightarrow AD \bot SB.$
Vẽ đường cao AH trong tam giác SAB
Lại có AD và AH qua A và vuông góc với SB.
Vậy mặt phẳng $\left( \alpha \right)$ chính là mặt phẳng (AHD)
Mặt khác AD // mp(SBC) mà $AD \subset mp\,\,\left( {AHD} \right)$
Vậy mặt phẳng (SBC) cắt mặt phẳng (AHD) theo giao tuyến HK // AD.
Do đó mặt cắt là hình thang ADKH mà $AD \bot mp\,\,\left( {SAB} \right)$$ \Rightarrow \,AD \bot AH.$
Suy ra tứ giác ADKH là hình thang vuông.
Tam giác SAB vuông $ \Rightarrow \,\,AH = \dfrac{{SA.AB}}{{SC}} = \dfrac{{a\sqrt 2 .a}}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}.$ Và $S{A^2} = SH.HB\,\, \Rightarrow \,\,SH = \dfrac{{S{A^2}}}{{SB}} = \dfrac{{2{a^2}}}{{a\sqrt 3 }} = \dfrac{{2a\sqrt 3 }}{3}.$
Ta có $HK$//$BC$$ \Rightarrow \,\,\dfrac{{HK}}{{BC}} = \dfrac{{SH}}{{SB}}\,\, \Rightarrow \,\,HK = \dfrac{{SH.BC}}{{SB}} = \dfrac{{\dfrac{{2a\sqrt 3 }}{3}.a}}{{a\sqrt 3 }} = \dfrac{{2a}}{3}.$
Do đó ${S_{ADKH}} = \dfrac{{AH}}{2}.\left( {HK + AD} \right) = \dfrac{{a\sqrt 6 }}{6}.\left( {\dfrac{{2a}}{3} + a} \right) = \dfrac{{a\sqrt 6 }}{6}.\dfrac{{5a}}{3} = \dfrac{{5{a^2}\sqrt 6 }}{{18}}.$

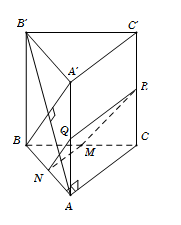
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $BC = a\sqrt 2 $; $AA' = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $M$ là trung điểm của $BC$ và vuông góc với $AB'$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình lăng trụ $ABC.A'B'C'$ là:
Gọi N là trung điểm $AB \Rightarrow MN//AC \Rightarrow MN \bot AB$.
Ta có $\left\{ \begin{array}{l}MN \bot AB\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {ABB'A'} \right) \Rightarrow MN \bot AB' \Rightarrow MN \subset \left( \alpha \right).$
Từ giả thiết $ \Rightarrow $$AB = a = AA' \Rightarrow ABB'A'$ là hình vuông $ \Rightarrow BA' \bot AB'$
Trong mp $\left( {ABB'A'} \right)$ kẻ $NQ\parallel BA'$ với $Q \in AA'$.
Trong mp $\left( {ACC'A'} \right)$ kẻ $QR\parallel AC$ với $R \in CC'$.
Vậy thiết diện là hình thang MNPQ vuông (do MN và QR cùng song song với AC và $MN \bot NQ$).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB = a,$ $BC = 2a.$ Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ đi qua $S$ vuông góc với $AB.$ Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.
|
Gọi H là trung điểm $AB \Rightarrow SH \bot AB.$ Suy ra: \( \bullet \) $SH \subset \left( \alpha \right)$. \( \bullet \) $SH \bot \left( {ABCD} \right)$ (do $\left( {SAB} \right) \bot \left( {ABCD} \right)$ theo giao tuyến $AB$). Kẻ $HM \bot AB{\rm{ }}\left( {M \in CD} \right) \Rightarrow HM \subset \left( \alpha \right).$ Do đó thiết diện là tam giác SHM vuông tại H. |
|
Ta có $SH = \dfrac{{a\sqrt 3 }}{2}$, $HM = BC = 2a.$ Vậy ${S_{\Delta SHM}} = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}.2a = \dfrac{{{a^2}\sqrt 3 }}{2}.$

Cho hình chóp đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, tâm $O$; $SO = 2a$. Gọi $M$ là điểm thuộc đoạn $AO{\rm{ }}\,\left( {M \ne A;M \ne O} \right)$. Mặt phẳng $\left( \alpha \right)$ đi qua $M$ và vuông góc với $AO$. Đặt $AM = x$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp $S.ABC.$
Vì S.ABC là hình chóp đều nên $SO \bot \left( {ABC} \right)$ ( với O là tâm của tam giác ABC).
Do đó $SO \bot AO$ mà $\left( \alpha \right) \bot AO$ suy ra $SO\parallel \left( \alpha \right)$.
Tương tự ta cũng có $BC\parallel \left( \alpha \right)$.
Qua M kẻ $IJ\parallel BC$ với $I \in AB,{\rm{ }}J \in AC$; kẻ $MK\parallel SO$ với $K \in SA.$
Khi đó thiết diện là tam giác KIJ.
Diện tích tam giác KIJ là ${S_{\Delta IJK}} = \dfrac{1}{2}IJ.MK$.
Trong tam giác ABC, ta có $\dfrac{{IJ}}{{BC}} = \dfrac{{AM}}{{AA'}}$ (A’ là trung điểm của BC) suy ra $IJ = \dfrac{{AM.BC}}{{AA'}} = \dfrac{{x.a}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{2x\sqrt 3 }}{3}$.
Tương tự trong tam giác SAO, ta có $\dfrac{{MK}}{{SO}} = \dfrac{{AM}}{{AO}}$ suy ra $MK = \dfrac{{AM.SO}}{{AO}} = \dfrac{{x.2a}}{{\dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2}}} = 2x\sqrt 3 $.
Vậy ${S_{\Delta IJK}} = \dfrac{1}{2}\dfrac{{2x\sqrt 3 }}{3}.2x\sqrt 3 = 2{x^2}$.