Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với $mp\,\,\left( {ABCD} \right).$ Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ và vuông góc với $SB.$ Mặt phẳng $\left( \alpha \right)$ cắt hình chóp theo thiết diện là hình gì ?
Trả lời bởi giáo viên
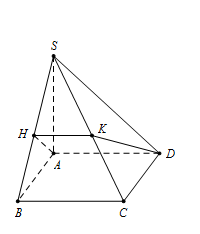
Ta có $AD$ vuông góc với $SA$ và $ AB$ $ \Rightarrow AD \bot mp\,\,\left( {SAB} \right) \Rightarrow AD \bot SB.$
Vẽ đường cao $AH$ trong tam giác $SAB$
Lại có $AD$ và $AH$ qua $A$ và vuông góc với $SB.$
Vậy mặt phẳng $\left( \alpha \right)$ chính là mặt phẳng $(AHD).$
Mặt khác $AD // mp(SBC) $ mà $AD \subset mp\,\,\left( {AHD} \right)$
Vậy mặt phẳng $(SBC)$ cắt mặt phẳng $(AHD) $ theo giao tuyến $HK // AD.$
Do đó mặt cắt là hình thang $ADKH $ mà $AD \bot mp\,\,\left( {SAB} \right)$$ \Rightarrow \,AD \bot AH.$
Vậy $ADKH $ là hình thang vuông.
Hướng dẫn giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng

