Cho lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều, chiều cao bằng \(\dfrac{1}{2}\) cạnh đáy. Thiết diện của hình lăng trụ và mặt phẳng qua $B'$ vuông góc với $A'C$ là
Trả lời bởi giáo viên
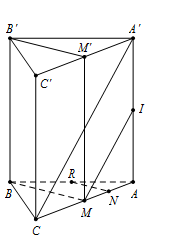
Gọi $M, M’, N, R$ lần lượt là trung điểm của $AC, A’C’, AM$ và $AB.$
Tam giác $A’B’C’$ đều suy ra $B'M' \bot A'C'.$
Mà $AA’$ vuông góc với đáy $(A’B’C’)$ $ \Rightarrow \,\,AA' \bot B'M'.$
Vậy $B’M’$ vuông góc với $(ACC’A’)$ $ \Rightarrow $$B'M' \bot A'C.$
Gọi $I$ là trung điểm của $AA’,$ ta có $A’C // MI.$
Mà $M’A’AM $ là hình vuông $ \Rightarrow \,\,M'N \bot MI.$
Do đó $M'N \bot A'C.$
Suy ra mặt cắt là $mp\,\,\left( {B'M'N} \right)$.
Mặt phẳng này cắt hai mặt phẳng song song $\left( {ABC} \right)$ và $\left( {A'B'C'} \right)$ theo hai giao tuyến $B’M’$ và $NR$ song song nhau.
Mặt khác $B'M' \bot \left( {ACC'A'} \right) \Rightarrow B'M' \bot M'N.$
Vậy $B’M’NR$ là hình thang vuông.
Hướng dẫn giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng

