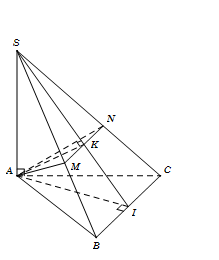
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a,$ $SA = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $A$ và vuông góc với trung tuyến $SI$ của tam giác $SBC$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.
Gọi I là trung điểm $BC \Rightarrow AI \bot BC.$ Kẻ $AK \bot SI$ $\left( {K \in SI} \right)$
\(\Delta SAB = \Delta SAC\left( {c.g.c} \right) \Rightarrow SB = SC \Rightarrow \Delta SBC\) cân tại S \( \Rightarrow SI \bot BC\)
Từ $K$ kẻ đường thẳng song song với $BC$ cắt $SB,{\rm{ }}SC$ lần lượt tạị $M,{\rm{ }}N$.
\( \Rightarrow MN \bot SI\). Khi đó thiết diện là tam giác $AMN.$
Ta có $\left\{ \begin{array}{l}BC \bot AI\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot AK \Rightarrow MN \bot AK.$
Tam giác vuông $SAI$, có $AK = \dfrac{{SA.AI}}{{\sqrt {S{A^2} + A{I^2}} }} = \dfrac{{a.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{a\sqrt {21} }}{7}$.
Tam giác $SBC$, có
$\dfrac{{MN}}{{BC}} = \dfrac{{SK}}{{SI}} = \dfrac{{S{A^2}}}{{S{I^2}}} = \dfrac{{S{A^2}}}{{S{A^2} + A{I^2}}} = \dfrac{{{a^2}}}{{{a^2} + {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}} = \dfrac{4}{7} \Rightarrow MN = \dfrac{{4a}}{7}.$
Vậy ${S_{\Delta AMN}} = \dfrac{1}{2}AK.MN = \dfrac{1}{2}\dfrac{{a\sqrt {21} }}{7}.\dfrac{{4a}}{7} = \dfrac{{2{a^2}\sqrt {21} }}{{49}}.$
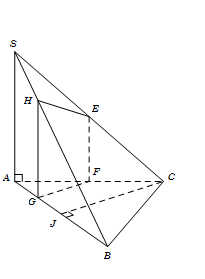
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $SA = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua trung điểm $E$ của $SC$ và vuông góc với $AB$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.
Gọi F là trung điểm AC, suy ra EF // SA.
Do $SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB$ nên $EF \bot AB$. \(\left( 1 \right)\)
Gọi J, G lần lượt là trung điểm AB, AJ.
Suy ra $CJ \bot AB$ và $FG\parallel CJ$ nên $FG \bot AB$. \(\left( 2 \right)\)
Trong $\Delta \,SAB$ kẻ $GH\parallel SA$ $\left( {H \in SB} \right)$, suy ra $GH \bot AB$. \(\left( 3 \right)\)
Từ \(\left( 1 \right)\) , \(\left( 2 \right)\) và \(\left( 3 \right)\), suy ra thiết diện cần tìm là hình thang vuông EFGH, vuông tại G và F.
Do đó ${S_{EFGH}} = \dfrac{1}{2}\left( {EF + GH} \right).FG$.
Ta có $EF = \dfrac{1}{2}SA = \dfrac{a}{2}$; $FG = \dfrac{1}{2}CJ = \dfrac{{a\sqrt 3 }}{4}$; $\dfrac{{GH}}{{SA}} = \dfrac{{BG}}{{BA}} = \dfrac{3}{4} \Rightarrow GH = BG = \dfrac{{3a}}{4}.$
Vậy ${S_{EFGH}} = \dfrac{1}{2}\left( {\dfrac{a}{2} + \dfrac{{3a}}{4}} \right).\dfrac{{a\sqrt 3 }}{4} = \dfrac{{5{a^2}\sqrt 3 }}{{32}}$.
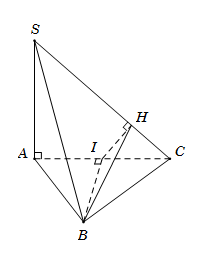
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $\,SA = 2a$ và vuông góc với đáy. Gọi $\left( \alpha \right)$ là mặt phẳng đi qua $B$ và vuông góc với $SC$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.
Gọi I là trung điểm của AC, suy ra $BI \bot AC$.
Ta có $\left\{ \begin{array}{l}BI \bot AC\\BI \bot SA\end{array} \right. \Rightarrow BI \bot \left( {SAC} \right) \Rightarrow BI \bot SC$. (1)
Kẻ $IH \bot SC$ $\left( {H \in SC} \right)$. (2)
Từ (1) và (2), suy ra $SC \bot \left( {BIH} \right)$.
Vậy thiết diện cần tìm là tam giác IBH.
Do $BI \bot \left( {SAC} \right) \Rightarrow BI \bot IH$ nên $\Delta \,IBH$ vuông tại I.
Ta có BI đường cao của tam giác đều cạnh a nên $BI = \dfrac{{a\sqrt 3 }}{2}$
Tam giác CHI đồng dạng tam giác CAS, suy ra
$\dfrac{{IH}}{{SA}} = \dfrac{{CI}}{{CS}} \Rightarrow IH = \dfrac{{CI.SA}}{{CS}} = \dfrac{{CI.SA}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{\dfrac{a}{2}.2a}}{{\sqrt {4{a^2} + {a^2}} }} = \dfrac{{a\sqrt 5 }}{5}$
Vậy ${S_{\Delta \,BIH}} = \dfrac{1}{2}BI.IH = \dfrac{1}{2}\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 5 }}{5} = \dfrac{{{a^2}\sqrt {15} }}{{20}}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$, đáy lớn $AD = 8$, $BC = 6$, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$, $SA = 6.$ Gọi $M$ là trung điểm $AB.$ Gọi $\left( P \right)$ là mặt phẳng qua $M$ và vuông góc với $AB$. Thiết diện của $\left( P \right)$ và hình chóp có diện tích bằng:
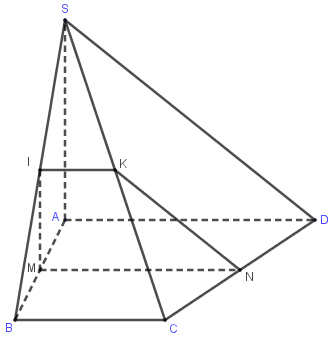
Do $\left( P \right) \bot AB \Rightarrow \left( P \right)\parallel SA.$
Gọi $I$ là trung điểm của $SB \Rightarrow MI\parallel SA \Rightarrow MI \subset \left( P \right).$
Gọi $N$ là trung điểm của $CD \Rightarrow MN \bot AB \Rightarrow MN \subset \left( P \right).$
Gọi $K$ là trung điểm của $SC \Rightarrow IK\parallel BC$,
Mà $MN\parallel BC \Rightarrow MN\parallel IK \Rightarrow IK \subset \left( P \right).$
Vậy thiết diện của $(P)$ và hình chóp là hình thang $MNKI$ vuông tại $M$ và $I.$
Ta có: $MI$ là đường trung bình của tam giác $SAB$ $ \Rightarrow MI = \dfrac{1}{2}SA = 3.$
$IK$ là đường trung bình của tam giác $SBC$ $ \Rightarrow IK = \dfrac{1}{2}BC = 3.$
$MN$ là đường trung bình của hình thang $ABCD$ $ \Rightarrow MN = \dfrac{1}{2}\left( {AD + BC} \right) = 7.$
Vậy ${S_{MNKI}} = \dfrac{{IK + MN}}{2}.MI = \dfrac{{3 + 7}}{2}.3 = 15.$
Cho hình chóp đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, tâm $O$, đường cao $AA'$; $SO = 2a$. Gọi $M$ là điểm thuộc đoạn $OA'{\rm{ }}\left( {M \ne A';M \ne O} \right)$. Mặt phẳng $\left( \alpha \right)$ đi qua $M$ và vuông góc với $AA'$. Đặt $AM = x$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp $S.ABC$.

Vì $S.ABC$ là hình chóp đều nên $SO \bot \left( {ABC} \right)$
($O$ là tâm của tam giác $ABC$)
Do đó $SO \bot AA'$ mà $\left( \alpha \right) \bot AA'$ suy ra $SO\parallel \left( \alpha \right)$.
Tương tự ta cũng có $BC\parallel \left( \alpha \right)$
Qua $M $ kẻ $IJ\parallel BC$ với $I \in AB,{\rm{ }}J \in AC$; kẻ $MN\parallel SO$ với $N \in SA'.$
Qua $N$ kẻ $EF\parallel BC$ với $E \in SB,{\rm{ }}F \in SC$.
Khi đó thiết diện là hình thang $IJFE.$
Diện tích hình thang ${S_{IJEF}} = \dfrac{1}{2}\left( {IJ + EF} \right)MN$.
Tam giác $ABC,$ có $\dfrac{{IJ}}{{BC}} = \dfrac{{AM}}{{AA'}} \Rightarrow IJ = \dfrac{{AM.BC}}{{AA'}} = \dfrac{{x.a}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{2x\sqrt 3 }}{3}.$
Tam giác $SBC,$ có $\dfrac{{EF}}{{BC}} = \dfrac{{SN}}{{SA'}} = \dfrac{{OM}}{{OA'}} \Rightarrow EF = \dfrac{{OM.BC}}{{OA'}} = \dfrac{{\left( {x - \dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2}} \right)a}}{{\dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}}} = 2\left( {x\sqrt 3 - a} \right).$
Tam giác $SOA’,$ có $\dfrac{{MN}}{{SO}} = \dfrac{{MA'}}{{OA'}} \Rightarrow MN = \dfrac{{SO.MA'}}{{OA'}} = \dfrac{{2a.\left( {\dfrac{{a\sqrt 3 }}{2} - x} \right)}}{{\dfrac{1}{3}\dfrac{{a\sqrt 3 }}{2}}} = 2\left( {3a - 2x\sqrt 3 } \right).$
Vậy
$\begin{array}{l}{S_{IJEF}} = \dfrac{1}{2}MN\left( {EF + IJ} \right) = \dfrac{1}{2}.2\left( {3a - 2x\sqrt 3 } \right)\left( {\dfrac{{2x\sqrt 3 }}{3} + 2\left( {x\sqrt 3 - a} \right)} \right)\\ = \dfrac{2}{3}\left( {4x\sqrt 3 - 3a} \right)\left( {3a - 2x\sqrt 3 } \right) = - 2\left( {8{x^2} - 6\sqrt 3 ax + 3{a^2}} \right).\end{array}$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB = a$, $AD = a\sqrt 3 $. Cạnh bên $SA = 2a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ đi qua $A$ vuông góc với $SC$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.
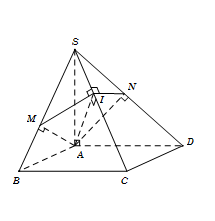
Trong tam giác $SAC, $ kẻ $AI \bot SC$ $\left( {\,I \in SC} \right)$
Trong $mp(SBC),$ kẻ ${d_1}$ đi qua $I$ vuông góc với $SC$ cắt $SB $ tại $M.$
Trong $mp(SCD),$ kẻ ${d_2}$ đi qua $I$ vuông góc với $SC$ cắt $SD$ tại $N.$
Khi đó thiết diện của hình chóp cắt bởi mp $\left( \alpha \right)$ là tứ giác $AMIN.$
Ta có $SC \bot \left( \alpha \right) \Rightarrow SC \bot AM$. (1)
Lại có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM$. (2)
Từ (1) và (2), suy ra $AM \bot \left( {SBC} \right) \Rightarrow AM \bot MI$. Chứng minh tương tự, ta được $AN \bot NI$.
Do đó ${S_{AMIN}} = {S_{\Delta AMI}} + {S_{\Delta ANI}} $ $= \dfrac{1}{2}AM.MI + \dfrac{1}{2}AN.NI$.
Vì $AM, AI, AN $ là các đường cao của các tam giác vuông $SAB, SAC, SAD $ nên
$AM = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$; $AI = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = a\sqrt 2 $; $AN = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{2a\sqrt {21} }}{7}$
Suy ra $MI = \sqrt {A{I^2} - A{M^2}} = \dfrac{{a\sqrt {30} }}{5}$ và $NI = \sqrt {A{I^2} - A{N^2}} = \dfrac{{a\sqrt {14} }}{7}$
Vậy ${S_{AMIN}} = \dfrac{1}{2}\left( {\dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{a\sqrt {30} }}{5} + \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{a\sqrt {14} }}{7}} \right) = \dfrac{{12{a^2}\sqrt 6 }}{{35}}$

