Câu hỏi:
2 năm trước
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA=a và vuông góc với đáy. Mặt phẳng (α) qua trung điểm E của SC và vuông góc với AB. Tính diện tích S của thiết diện tạo bởi (α) với hình chóp đã cho.
Trả lời bởi giáo viên
Đáp án đúng: c
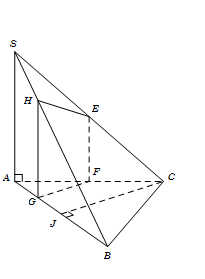
Gọi F là trung điểm AC, suy ra EF // SA.
Do SA⊥(ABC)⇒SA⊥AB nên EF⊥AB. (1)
Gọi J, G lần lượt là trung điểm AB, AJ.
Suy ra CJ⊥AB và FG∥CJ nên FG⊥AB. (2)
Trong ΔSAB kẻ GH∥SA (H∈SB), suy ra GH⊥AB. (3)
Từ (1) , (2) và (3), suy ra thiết diện cần tìm là hình thang vuông EFGH, vuông tại G và F.
Do đó SEFGH=12(EF+GH).FG.
Ta có EF=12SA=a2; FG=12CJ=a√34; GHSA=BGBA=34⇒GH=BG=3a4.
Vậy SEFGH=12(a2+3a4).a√34=5a2√332.
Hướng dẫn giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác
