Giới hạn của dãy số

Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I₁ đi vào tại A, dòng I₂ đi ra tại B thì các dòng điện \({I_1}\) và \({I_2}\)  gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to  \)và \(\mathop {{B_2}}\limits^ \to  \)có phương chiều như hình vẽ:

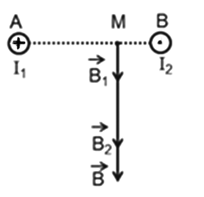
Có độ lớn: \(\left\{ \begin{array}{l}{B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {2.10^{ - 7}}\dfrac{{12}}{{{{15.10}^{ - 2}}}}{\rm{ =  }}1,{6.10^{ - 5}}T\\{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{BM}} = {2.10^{ - 7}}\dfrac{{15}}{{{{5.10}^{ - 2}}}}{\rm{ =  }}{6.10^{ - 5}}T\end{array} \right.\)

Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to   = \mathop {{B_1}}\limits^ \to   + \mathop {{B_2}}\limits^ \to  \) .

Vì \(\mathop {{B_1}}\limits^ \to  \)và \(\mathop {{B_2}}\limits^ \to  \)cùng phương, cùng chiều \( \Rightarrow B = {B_1} + {B_2} = 1,{6.10^{ - 5}} + {6.10^{ - 5}} = 7,{6.10^{ - 5}}T\)

Dãy số \(\left( {{u_n}} \right)\) có giới hạn \(0\) ta có thể viết:

\(\mathop {\lim }\limits_{n \to  + \infty } \left( {{u_n}} \right) = 0\), viết tắt là \(\lim \left( {{u_n}} \right) = 0\) hoặc \(\lim {u_n} = 0\).

Ta có : \(\lim \dfrac{{{u_n} + 1}}{{3u_n^2 + 5}} = \lim \dfrac{{u_n^2\left( {\dfrac{1}{{{u_n}}} + \dfrac{1}{{u_n^2}}} \right)}}{{u_n^2\left( {3 + \dfrac{5}{{u_n^2}}} \right)}}\) \( = \lim \dfrac{{\dfrac{1}{{{u_n}}} + \dfrac{1}{{u_n^2}}}}{{3 + \dfrac{5}{{u_n^2}}}} = \dfrac{{0 + 0}}{{3 + 0}} = 0\).

Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn \(0\) nếu mọi số hạng của dãy số đều có giá trị tuyệt đối nhỏ hơn một số dương nhỏ tùy ý cho trước kể từ một số hạng nào đó trở đi.

Bước 1: Tìm cấp số nhân

Ta biểu diễn \(b = 8,020202... = 8 + \underbrace {\underbrace {\underbrace {0,02}_{{u_1}}02}_{{u_2}}02}_{{u_3}}...\)

\( = 8 + \dfrac{2}{{100}} + \dfrac{2}{{{{100}^2}}} + \dfrac{2}{{{{100}^3} }}+ ...\)

Xét $S=\dfrac{2}{100}+\dfrac{2}{100^{2}}+\dfrac{2}{100^{3}}+\ldots$

Suy ra: $S$ là tổng của một cấp số nhân lùi vô hạn biết:

- Số hạng đầu: $u_{1}=\dfrac{2}{100}$.

- Công bội: $q=\dfrac{1}{100}$

Bước 2: Sử dụng công thức tổng cấp số nhân lùi vô hạn

Do vậy: $S=\dfrac{u_{1}}{1-q}=\dfrac{\dfrac{2}{100}}{1-\dfrac{1}{100}}=\dfrac{2}{99}$.

Vậy: $b=8+\dfrac{2}{99}=\dfrac{794}{99}$.

Dễ thấy \(\lim {u_n} = 0\) nên A đúng.

Do \(\left| {\dfrac{{{{\left( { - 1} \right)}^n}}}{n}} \right| \le \dfrac{1}{n}\) và \(\lim \dfrac{1}{n} = 0\) nên \(\lim \dfrac{{{{\left( { - 1} \right)}^n}}}{n} = 0\) hay \(\lim {v_v} = 0\).

Do đó các đáp án B và C đúng.

Ta thấy: $\dfrac{1}{{{2^n}}} = {\left( {\dfrac{1}{2}} \right)^n};\dfrac{1}{{{3^n}}} = {\left( {\dfrac{1}{3}} \right)^n},$ $\dfrac{1}{{{{\left( {0,5} \right)}^n}}} = {\left( {\dfrac{1}{{0,5}}} \right)^n} = {2^n},\dfrac{1}{{{{\left( {\sqrt 2 } \right)}^n}}} = {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^n}$

Mà \(\dfrac{1}{2} < 1,\dfrac{1}{3} < 1,\dfrac{1}{{\sqrt 2 }} < 1\) nên các đáp án A, B, D đúng.

Vì \(2 > 1\) nên \(\lim {2^n} =  + \infty \) nên C sai.

Vì \(\lim {u_n} =  - \dfrac{1}{2}\) nên \(\lim \left( {{u_n} + \dfrac{1}{2}} \right) = 0\).

Do \(\lim {u_n} = 1 - \sqrt 2 \) nên \(\lim \left| {{u_n}} \right| = \left| {1 - \sqrt 2 } \right| = \sqrt 2  - 1\).

Dễ thấy các đáp án A, B, C đúng theo định lý về dãy số có giới hạn hữu hạn.

Ta có: \(\lim \left( {{u_n} + {v_n}} \right) = \sqrt 3  - 2\sqrt 3  =  - \sqrt 3  < 0\).

Đáp án A: \(\lim \left( {{u_n} - 2{v_n}} \right) = \dfrac{5}{3} - 2.\left( { - \dfrac{2}{3}} \right) = 3 \ne \dfrac{1}{3}\) nên A sai.

Đáp án B: \(\lim \left( {2{u_n} - {v_n}} \right) = 2.\dfrac{5}{3} - \left( { - \dfrac{2}{3}} \right) = 4\) nên B đúng.

Đáp án C: \(\lim \left( {{u_n} - {v_n}} \right) = \dfrac{5}{3} - \left( { - \dfrac{2}{3}} \right) = \dfrac{7}{3} \ne 1\) nên C sai.

Đáp án D: \(\lim \left( {{u_n} + {v_n}} \right) = \dfrac{5}{3} + \left( { - \dfrac{2}{3}} \right) = 1 \ne \dfrac{1}{3}\) nên D sai.

Do \(0 < q = \dfrac{1}{3} < 1\) nên:

\({S_n} = {u_1} + {u_2} + ... + {u_n} = \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)  \( \Rightarrow \lim {S_n} = \lim \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}} = \dfrac{{{u_1}}}{{1 - q}} = \dfrac{2}{{1 - \dfrac{1}{3}}} = 3\)

Bước 1:

Vì \({S_n} = {u_1} + {u_2} + ... + {u_n}\) nên đây là tổng \(n\) số hạng đầu của cấp số nhân công bội \(q = \dfrac{1}{2}\).

Bước 2:

Theo công thức tính tổng \({S_n} = \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\) ta được \({S_n} = \dfrac{{2\left( {1 - {{\left( {\dfrac{1}{2}} \right)}^n}} \right)}}{{1 - \dfrac{1}{2}}} = 4\left( {1 - \dfrac{1}{{{2^n}}}} \right)\).

Dãy số \(\left( {{u_n}} \right)\) có giới hạn \( + \infty \) nếu mọi số hạng của dãy số đều lớn hơn một số dương tùy ý cho trước kể từ một số hạng nào đó trở đi.

Đáp án A: \(\lim \dfrac{1}{n} = 0\) nên loại.

Đáp án B: \(\lim \left( { - \sqrt n } \right) =  - \infty \) nên loại.

Đáp án C: \(\lim \left( {2{n^2}} \right) =  + \infty \) nên C đúng.

Đáp án D: \(\lim \left( {\dfrac{{ - 1}}{{2{n^2}}}} \right) = 0\) nên loại D.

Các dãy \(\left( {{u_n}} \right),\left( {{v_n}} \right),\left( {{x_n}} \right)\) đều là các dãy số không có giới hạn.

Dãy \(\left( {{y_n}} \right)\) mà \({y_n} = \dfrac{1}{2},\forall n \in {\mathbb{N}^*}\) có giới hạn \(\lim {y_n} = \dfrac{1}{2}\) nên đáp án D đúng.

\(\lim {S_n} = \dfrac{{{u_1}}}{{1 - q}} = \dfrac{3}{{1 + \dfrac{1}{2}}} = 2\)

\(\lim \left( {3{u_n} + 4{v_n}} \right) = 3.\left( { - 5} \right) + 4.4 = 1\)

Bước 1:

\(\begin{array}{l}S = {\left( {\dfrac{1}{2}} \right)^0} +{\left( {\dfrac{1}{2}} \right)^1} + {\left( {\dfrac{1}{2}} \right)^2} +  \cdots  + {\left( {\dfrac{1}{2}} \right)^{n - 1}} + ...\\ \Rightarrow q = \dfrac{1}{2}\end{array}\)

Bước 2:

\( \Rightarrow S = \dfrac{1}{{1 - \dfrac{1}{2}}} = 2\)