Giới hạn của dãy số

Bước 1:

Gọi \({h_n}\) là độ dài đường đi của quả bóng ở lần rơi xuống thứ \(n\left( {n \in {\mathbb{N}^*}} \right)\).

Gọi \({l_n}\) là độ dài đường đi của quả bóng ở lần nảy lên thứ \(n\left( {n \in {\mathbb{N}^*}} \right)\).

Bước 2: Tính \({h_1},{l_1}\). Từ đó tính S.

Theo bài ra ta có \({h_1} = 55,8,{l_1} = \dfrac{1}{{10}}.55,8 = 5,58\) và các dãy số \(\left( {{h_n}} \right),{l_n}\) là các cấp số nhân lùi vô hạn với công bội \(q = \dfrac{1}{{10}}\).

Suy ra tổng độ dài đường đi của quả bóng là

\(S = \dfrac{{{h_1}}}{{1 - \dfrac{1}{{10}}}} + \dfrac{{{l_1}}}{{1 - \dfrac{1}{{10}}}} = \dfrac{{10}}{9}\left( {{h_1} + {l_1}} \right) = 68,2(m)\)

Dãy số \(\left( {{u_n}} \right)\) mà \({u_n} = \dfrac{2}{n}\) có giới hạn \(0\).

Ta có: \(\lim \dfrac{{3{u_n} - 1}}{{{u_n} + 1}} = \dfrac{{3\lim {u_n} - 1}}{{\lim {u_n} + 1}}\) \( = \dfrac{{3.3 - 1}}{{3 + 1}} = \dfrac{8}{4} = 2\)

Các dãy số có giới hạn \(0\) là: \({u_n} = \dfrac{1}{{\sqrt n }},{u_n} = \dfrac{1}{{\sqrt[3]{n}}},{u_n} = 0\).

Dãy số \(\left( {{u_n}} \right)\) ở đáp án C có \(\lim {u_n} = \lim \dfrac{{\sqrt[3]{n}}}{2} =  + \infty \)

Định lý: Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\). Nếu \(\left| {{u_n}} \right| \le {v_n}\) với mọi \(n\) và \(\lim {v_n} = 0\) thì \(\lim {u_n} = 0\).

Định lý: Nếu \(\left| q \right| < 1\) thì \(\lim {q^n} = 0\).

Định nghĩa: Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là số thực \(L\) nếu \(\mathop {\lim }\limits_{n \to  + \infty } \left( {{u_n} - L} \right) = 0\).

Giả sử \(\lim {u_n} = L\). Khi đó \(\lim \left| {{u_n}} \right| = \left| L \right|\).

Định lý 1: Giả sử \(\lim {u_n} = L\). Khi đó:

i) \(\lim \left| {{u_n}} \right| = \left| L \right|\) và \(\lim \sqrt[3]{{{u_n}}} = \sqrt[3]{L}\).

ii) Nếu \({u_n} \ge 0\) với mọi \(n\) thì \(L \ge 0\) và \(\lim \sqrt {{u_n}} = \sqrt L \)

Từ định lý trên ta thấy chỉ có đáp án D đúng.

Giả sử \(\lim {u_n} = L,\lim {v_n} = M\). Khi đó \(\lim \left( {{u_n} + {v_n}} \right) = L + M\)

Giả sử \(\lim {u_n} = L,\lim {v_n} = M\) và \(c\) là một hằng số. Khi đó:

\(\lim \left( {{u_n} + {v_n}} \right) = L + M,\lim \left( {{u_n} - {v_n}} \right) = L - M,\lim \left( {{u_n}.{v_n}} \right) = L.M,\lim \left( {c.{u_n}} \right) = c.L\)

Công thức tính tổng cấp số nhân lùi vô hạn: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \dfrac{{{u_1}}}{{1 - q}}\).

Ta có: \({u_1} = \dfrac{1}{2};q = \dfrac{1}{2} \Rightarrow S = \dfrac{{{u_1}}}{{1 - q}} = \dfrac{{\dfrac{1}{2}}}{{1 - \dfrac{1}{2}}} = 1\)

Dãy số \(\left( {{u_n}} \right)\) có giới hạn \( - \infty \) nếu mọi số hạng của dãy số đều nhỏ hơn một số âm tùy ý cho trước kể từ một số hạng nào đó trở đi.

Khi đó, ta viết \(\mathop {\lim }\limits_{n \to  + \infty } \left( {{u_n}} \right) =  - \infty \), viết tắt là \(\lim \left( {{u_n}} \right) =  - \infty \) hoặc \(\lim {u_n} =  - \infty \).

Ta có: \(\lim n =  + \infty ,\lim \sqrt n  =  + \infty ,\) \(\lim \sqrt[3]{n} =  + \infty ,\) \(\lim \dfrac{1}{n} =  0 \)

Vậy chỉ có đáp án D là sai.

Ta có: \(\lim \left( {{u_n}.{v_n}} \right) = \lim \left( {\dfrac{1}{n}.{n^2}} \right) = \lim n =  + \infty \).

\(\sqrt 2  > 1 =  > \lim {(\sqrt 2 )^n} =  + \infty \)

Đáp án A sai.

\(\begin{array}{l}S = {u_1} + {u_2} + ...\\ = {u_1}\left( {1 + q + {q^2} + ...} \right)\\ = \dfrac{{{u_1}}}{{1 - q}}\end{array}\)

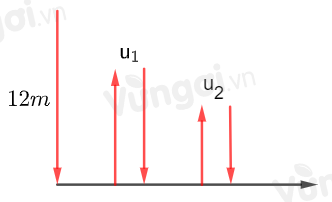
Ta coi độ cao nảy lên lần thứ nhất là \({u_1} \Rightarrow {u_1} = 12.\dfrac{2}{3} = 8\)

\( \Rightarrow {u_2} = \dfrac{2}{3}{u_1};{u_3} = \dfrac{2}{3}{u_2};...;{u_n} = \dfrac{2}{3}{u_{n - 1}};...\)

=> Đây là cấp số nhân lùi vô hạn với \({u_1} = 8;q = \dfrac{2}{3}\)

Khi đó tổng quãng đường quả bóng đã di chuyển là

\(S = 12 + 2{u_1} + 2{u_2} + 2{u_3} + ... + 2{u_n} + ...\)

$=12+2.(u_1+u_2+…)$$=12+2.\dfrac{u_1}{1-q}$

\( = 12 + 2.\dfrac{8}{{1 - \dfrac{2}{3}}} = 60\)

Bước 1: Tìm cấp số nhân

Ta biểu diễn

\(a = \underbrace {\underbrace {\underbrace {0,1}_{{u_1}}1}_{{u_2}}1}_{{u_3}}... = 0,1 + 0,01 + 0,001 + ...\)\( = \dfrac{1}{{10}} + \dfrac{1}{{{{10}^2}}} + \dfrac{1}{{{{10}^3}}} + ...\)

Xét dãy \({u_1} = 0,1;{u_2} = 0,01;{u_3} = 0,001;\)\(...;{u_n} = 0,\underbrace {0...01}_{n\,{\rm{ chữ\, số}}};...\)

Ta thấy dãy trên có:

- Số hạng đầu: $u_{1}=0,1=\dfrac{1}{10}$.

- Số hạng thứ hai \({u_2}=0,01 = \dfrac{1}{{{{10}^2}}} = {u_1}.\dfrac{1}{{10}}\)

- Số hạng thứ n: \({u_n}=0,\underbrace {0...01}_{n\,{\rm{ chữ\, số}}} = \dfrac{1}{{{{10}^n}}} = {u_1}.{\left( {\dfrac{1}{{10}}} \right)^{n - 1}}\)

Bước 2: Sử dụng công thức tổng cấp số nhân lùi vô hạn

Như vậy $a$ là tổng của một cấp số nhân lùi vô hạn biết:

- Số hạng đầu: $u_{1}=\dfrac{1}{10}$.

- Công bội: $q=\dfrac{1}{10}$

Do vậy: $a=\dfrac{u_{1}}{1-q}=\dfrac{\dfrac{1}{10}}{1-\dfrac{1}{10}}=\dfrac{1}{9}$.

Vậy: $a=\dfrac{1}{9}$.