Câu hỏi:
2 năm trước
Hai dòng điện thẳng dài, đặt song song ngược chiều, cách nhau 20cm trong không khí có \({I_1} = 12A\), \({I_2} = 15A\). Xác định cảm ứng từ tổng hợp tại điểm M cách \({I_1}\) \(15cm\) và cách \({I_2}\) là \(5cm\)?
Trả lời bởi giáo viên
Đáp án đúng: c
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi ra tại B thì các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \)và \(\mathop {{B_2}}\limits^ \to \)có phương chiều như hình vẽ:
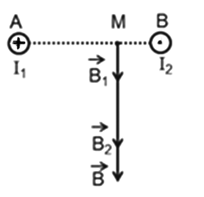
Có độ lớn: \(\left\{ \begin{array}{l}{B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {2.10^{ - 7}}\dfrac{{12}}{{{{15.10}^{ - 2}}}}{\rm{ = }}1,{6.10^{ - 5}}T\\{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{BM}} = {2.10^{ - 7}}\dfrac{{15}}{{{{5.10}^{ - 2}}}}{\rm{ = }}{6.10^{ - 5}}T\end{array} \right.\)
Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) .
Vì \(\mathop {{B_1}}\limits^ \to \)và \(\mathop {{B_2}}\limits^ \to \)cùng phương, cùng chiều \( \Rightarrow B = {B_1} + {B_2} = 1,{6.10^{ - 5}} + {6.10^{ - 5}} = 7,{6.10^{ - 5}}T\)
Hướng dẫn giải:
+ Áp dụng các bước giải xác định cảm ứng từ (Xem lí thuyết phần V)
+ Áp dụng biểu thức xác định cảm ứng từ của dòng điện thẳng: \(B = {2.10^{ - 7}}\dfrac{I}{r}\)
+ Sử dụng nguyên lý chồng chất từ trường
