Cho tam giác cân $ABC,$ $AB = AC = a\sqrt 5 $ $BC = 4a.$ Trên nửa đường thẳng vuông góc với mặt phẳng chứa tam giác $ABC$ tại $A$ lấy một điểm $D$ sao cho $AD = a\sqrt 3 .$ Người ta cắt hình chóp bằng một mặt phẳng $\left( P \right)$ vuông góc với đường cao $AH$ của tam giác $ABC.$ Thiết diện là hình gì ?
Trả lời bởi giáo viên
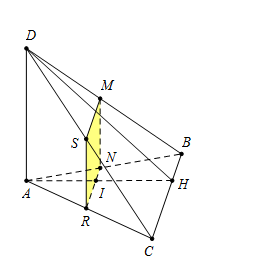
Ta có $AH$ vuông góc với $BC$ và $AD.$
Vậy $(P)$ là mặt phẳng song song với $BC$ và $AD.$
Lại có $BC // (P)$ nên $(P)$ cắt hai mặt phẳng $(ABC)$ và $(DBC)$ theo hai giao tuyến $NR$ và $MS$ với $NR // MS // BC.$
Mà $AD // (P)$ nên $\left( P \right)$ cắt hai mặt phẳng $(ACD)$ và $(BAD)$ theo hai giao tuyến $RS$ và $NM$ với $RS // MN // AD.$
Mặt khác $NM // AD$ và $AD \bot NR$\( \Rightarrow MN \bot NR\) suy ra $MNRS$ là hình chữ nhật.
Hướng dẫn giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng

