Cho tứ diện $SABC$ có hai tam giác $\Delta ABC$ và $\Delta SBC$ là hai tam giác đều cạnh $a,\,\,\,SA = \dfrac{{a\sqrt 3 }}{2}.$ Gọi $M$ là điểm trên $AB$ sao cho $AM = b{\rm{ }}\left( {0 < b < a} \right).$ $\left( P \right)$ là mặt phẳng qua $M$ và vuông góc với $BC.$ Thiết diện của $\left( P \right)$ và tứ diện $SABC$ có diện tích bằng ?
Trả lời bởi giáo viên
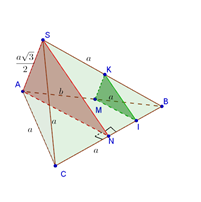
Gọi $N$ là trung điểm của $BC.$
Ta có \(\left\{ \begin{array}{l}SB = SC\\AB = AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}BC \bot SN\\BC \bot AN\end{array} \right. \Rightarrow BC \bot \left( {SAN} \right).\)
Theo bài ra \(BC \bot \left( P \right) \Rightarrow \left\{ \begin{array}{l}M \in \left( P \right)\\\left( P \right)//\left( {SAN} \right)\end{array} \right.\).
Kẻ \(MI//AN,\,MK//SA\)
\( \Rightarrow \) Thiết diện của $\left( P \right)$ và $S.ABC$ là \(\Delta KMI\)
Mà \(\left\{ \begin{array}{l}\Delta ABC\\\Delta SBC\end{array} \right.\) là hai tam giác đều cạnh $a$
$\Rightarrow AN = SN = \dfrac{{a\sqrt 3 }}{2} = SA $ $\Rightarrow \Delta SAN$ là tam giác đều cạnh \(\dfrac{{a\sqrt 3 }}{2}\)
\(\Rightarrow \Delta KMI\) là tam giác đều cạnh \(\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a - b}}{a}= \frac{{\sqrt 3 }}{2}\left( {a - b} \right)\)
\(\Rightarrow {S_{\Delta KMI}} = \dfrac{{3\sqrt 3 }}{{16}}(a-b)^2\)
Hướng dẫn giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, cụ thể là tính diện tích

