Số vị trí biểu diễn các nghiệm của phương trình \(\sin \left( {2x + \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\) trên đường tròn lượng giác là?
Trả lời bởi giáo viên
Phương trình \( \Leftrightarrow \sin \left( {2x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{3} = \dfrac{\pi }{6} + k2\pi \\2x + \dfrac{\pi }{3} = \pi - \dfrac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{\pi }{4} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\)
Biểu diễn nghiệm \(x = - \dfrac{\pi }{{12}} + k\pi \) trên đường tròn lượng giác ta được 2 vị trí (hình 1).
Biểu diễn nghiệm \(x = \dfrac{\pi }{4} + k\pi \) trên đường tròn lượng giác ta được 2 vị trí (hình 2).
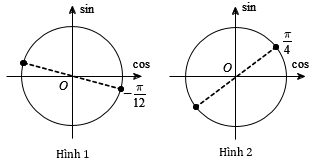
Vậy có tất cả 4 vị trí biểu diễn các nghiệm các nghiệm của phương trình.
Hướng dẫn giải:
- Giải phương trình \(\sin \left( {2x + \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\)
- Biểu diễn các nghiệm trên đường tròn lượng giác và kết luận.

