Câu hỏi:
3 năm trước
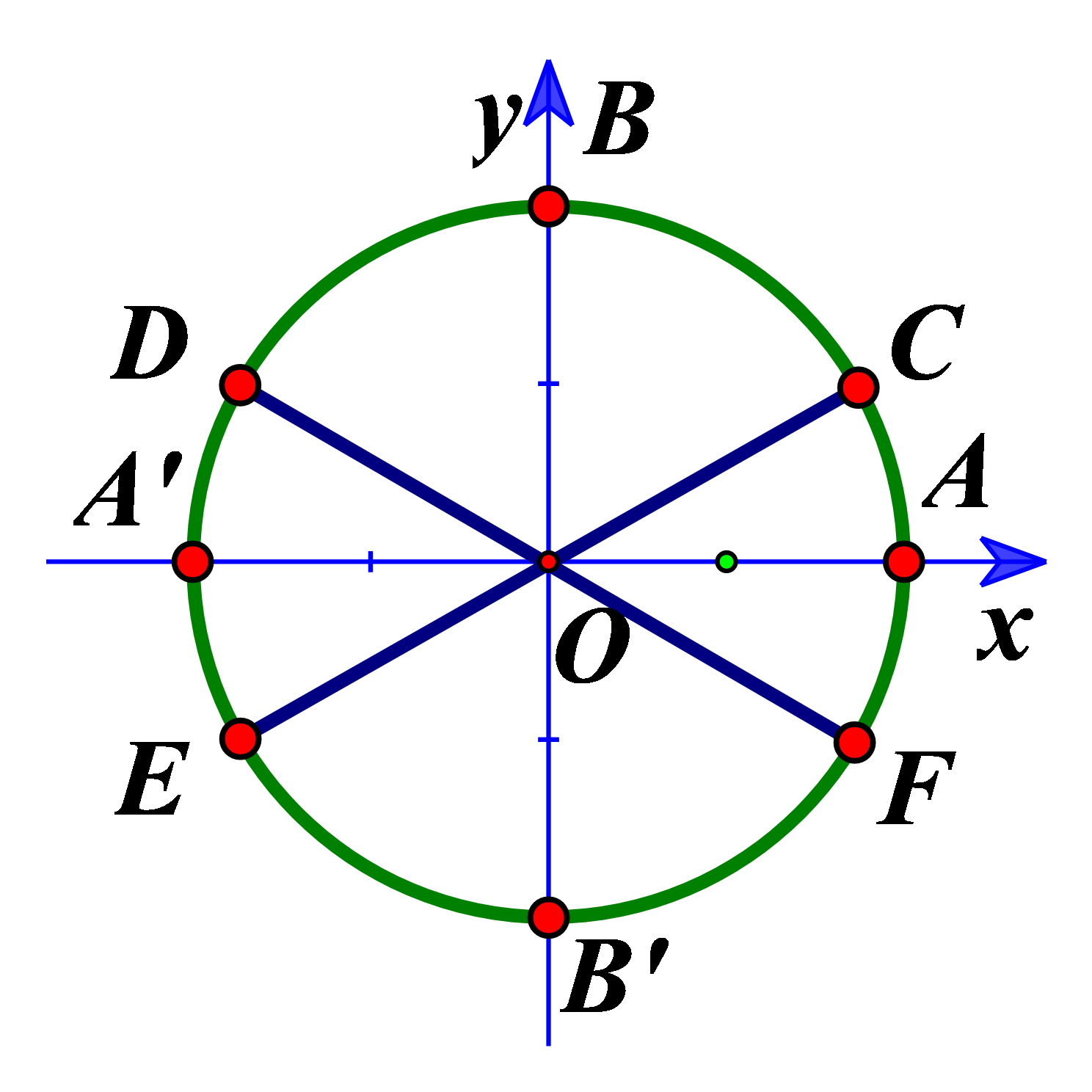
Nghiệm của phương trình \(2\sin x + 1 = 0\) được biểu diễn trên đường tròn lượng giác ở hình trên là những điểm nào?
Trả lời bởi giáo viên
Đáp án đúng: b
Bước 1: Tìm x
Ta có \(2\sin x + 1 = 0 \Leftrightarrow \sin x = - \dfrac{1}{2}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - \dfrac{\pi }{6} + k2\pi }\\{x = \dfrac{{7\pi }}{6} + k2\pi }\end{array}(k \in \mathbb{Z})} \right.\).
Bước 2: Tìm k từ đó tìm các điểm biểu diễn.
Với \(k = 0 \Rightarrow x = - \dfrac{\pi }{6}\) hoặc \(x = \dfrac{{7\pi }}{6}\).
Điểm biểu diễn của \(x = - \dfrac{\pi }{6}\) là \(F\), điểm biểu diễn \(x = \dfrac{{7\pi }}{6}\) là \(E\).
Hướng dẫn giải:
Bước 1: Tìm x
Bước 2: Tìm k từ đó tìm các điểm biểu diễn.

