Một số phương trình lượng giác thường gặp

Ta có

$4{\cos ^3}x - \cos 2x$$+ (m - 3)\cos x - 1 = 0$$\Leftrightarrow 4{\cos ^3}x - 2{\cos ^2}x$$+ (m - 3)\cos x = 0$

$\Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos x = 0}\\{4{{\cos }^2}x - 2\cos x + m - 3 = 0(1)}\end{array}} \right.$

$\cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}$ không có nghiệm thuộc khoảng $\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)$.

Đặt $t = \cos x$, vì $x \in \left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)$ nên $t \in (0;1]$.

Khi đó phương trình (1) $\Leftrightarrow 4{t^2} - 2t + m - 3 = 0$

Khi đó yêu cầu bài toán tương đương với tìm số các giá trị nguyên của m để phương trình (2) có 2 nghiệm phân biệt ${t_1},{t_2}$ thỏa mãn $0 < {t_1},{t_2} < 1$.

(2) $\Leftrightarrow m =  - 4{t^2} + 2t + 3 = g(t)$

Ta có bảng biến thiên của $g(t)$ trên $t \in (0;1]$.

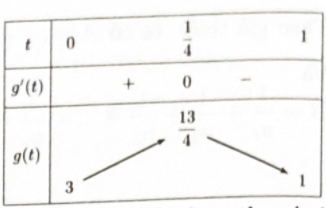
Từ bảng biến thiên trên ta có:

Phương trình (2) có 2 nghiệm phân biệt ${t_1},{t_2}$ thỏa mãn $0 < {t_1},{t_2} < 1$ thì $3 < m < \dfrac{{13}}{4}$. Vì $m$ nguyên nên không có giá trị nào.

Bước 1:

${\sin ^2}x - 3\sin x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\sin x = 2\left( {Loai} \right)\end{array} \right.$

Bước 2:

$\Leftrightarrow x = \dfrac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)$

Bước 1:

$4{\cos ^2}\dfrac{x}{2} - \sqrt 3 \cos 2x$$= 1 + 2{\cos ^2}\left( {x - \dfrac{\pi }{4}} \right)$

$\Leftrightarrow 2\left( {1 + \cos x} \right) - \sqrt 3 \cos 2x$$= 1 + 1 + \cos \left( {2x - \dfrac{\pi }{2}} \right)$

$\begin{array}{l} \Leftrightarrow 2 + 2\cos x - \sqrt 3 \cos 2x = 2 + \sin 2x\\ \Leftrightarrow 2\cos x = \sin 2x + \sqrt 3 \cos 2x\end{array}$

Bước 2:

$\begin{array}{l} \Leftrightarrow \cos x = \dfrac{1}{2}\sin 2x + \dfrac{{\sqrt 3 }}{2}\cos 2x\\ \Leftrightarrow \cos x = \cos 2x\cos \dfrac{\pi }{6} + \sin 2x\sin \dfrac{\pi }{6}\\ \Leftrightarrow \cos x = \cos \left( {2x - \dfrac{\pi }{6}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x - \dfrac{\pi }{6} = x + k2\pi \\2x - \dfrac{\pi }{6} =  - x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Xét $x = \dfrac{\pi }{6} + k2\pi$ thuộc $\left( {0;\dfrac{\pi }{2}} \right)$

$\Leftrightarrow 0 < \dfrac{\pi }{6} + k2\pi  < \dfrac{\pi }{2}$$\Leftrightarrow  - \dfrac{1}{{12}} < k < \dfrac{1}{6}$

Vì k nguyên nên $k = 0 \Rightarrow x = \dfrac{\pi }{6}$

Xét $x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}$ thuộc $\left( {0;\dfrac{\pi }{2}} \right)$

$\Leftrightarrow 0 < \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3} < \dfrac{\pi }{2}$$\Leftrightarrow  - \dfrac{1}{{12}} < k < \dfrac{2}{3}$

Vì k nguyên nên $k = 0 \Rightarrow x = \dfrac{\pi }{{18}}$

Vậy các nghiệm của phương trình thuộc $\left( {0;\dfrac{\pi }{2}} \right)$ là $\left\{ {\dfrac{\pi }{6};\dfrac{\pi }{{18}}} \right\}$.

Bước 1:

$\sin 2x - \sqrt 3 \sin x = 0$$\Leftrightarrow 2\sin x\cos x - \sqrt 3 \sin x = 0$

$\Leftrightarrow \sin x\left( {2\cos x - \sqrt 3 } \right) = 0$$\Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = \dfrac{{\sqrt 3 }}{2}\end{array} \right.$

Bước 2:

$\Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = \cos \dfrac{\pi }{6}\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x =  \pm \dfrac{\pi }{6} + k2\pi \end{array} \right.,k \in \mathbb{Z}$

Bước 1:

ĐK: $\cos x \ne 0$.

$1 + {\rm{sin}}x + {\rm{cos}}x + {\rm{tan}}x = 0$ $\Leftrightarrow \left( {1 + \tan x} \right) + \left( {\sin x + \cos x} \right) = 0$

$\Leftrightarrow \left( {1 + \dfrac{{\sin x}}{{\cos x}}} \right) + \left( {\sin x + \cos x} \right) = 0$

$\Leftrightarrow \dfrac{{\sin x + \cos x}}{{\cos x}} + \left( {\sin x + \cos x} \right) = 0$

$\Leftrightarrow \left( {\sin x + \cos x} \right)\left( {\dfrac{1}{{\cos x}} + 1} \right) = 0$

$\Leftrightarrow \left( {\sin x + \cos x} \right).\dfrac{{1 + \cos x}}{{\cos x}} = 0$

Bước 2:

$\Leftrightarrow \left[ \begin{array}{l}\sin x + \cos x = 0\\\cos x + 1 = 0\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}\sin x =  - \cos x\\\cos x =  - 1\end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}\dfrac{{\sin x}}{{\cos x}} =  - 1\\\cos x =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\tan x =  - 1\\\cos x =  - 1\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{4} + k\pi \\x = \pi  + k2\pi \end{array} \right.\left( {TM} \right)$

ĐK:  $\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi$.

$\begin{array}{l}{\sin ^2}x + {\sin ^2}x{\tan ^2}x = 3\\ \Leftrightarrow {\sin ^2}x\left( {1 + {{\tan }^2}x} \right) = 3\\ \Leftrightarrow {\sin ^2}x\left( {1 + \dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}} \right) = 3\\ \Leftrightarrow {\sin ^2}x\left( {\dfrac{{{{\cos }^2}x}}{{{{\cos }^2}x}} + \dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}} \right) = 3\\ \Leftrightarrow {\sin ^2}x\left( {\dfrac{{{{\cos }^2}x + {{\sin }^2}x}}{{{{\cos }^2}x}}} \right) = 3\\ \Leftrightarrow {\sin ^2}x.\dfrac{1}{{{{\cos }^2}x}} = 3\\ \Leftrightarrow {\tan ^2}x = 3\end{array}$

$\Leftrightarrow \left[ \begin{array}{l}\tan x = \sqrt 3 \\\tan x =  - \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\tan x = \tan \dfrac{\pi }{3}\\\tan x = \tan \left( { - \dfrac{\pi }{3}} \right)\end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{3} + k\pi \\x =  - \dfrac{\pi }{3} + k\pi \end{array} \right.$

Điều kiện: $\left\{ \begin{array}{l}x \ne \dfrac{\pi }{2} + k\pi \\y \ne \dfrac{\pi }{2} + k\pi \end{array} \right.$ .

Ta có $\left\{ \begin{array}{l}x + y = \dfrac{{2\pi }}{3}\\\tan x.\tan y = 3\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = \dfrac{{2\pi }}{3} - x}&{\left( 1 \right)}\\{\tan x.\tan \left( {\dfrac{{2\pi }}{3} - x} \right) = 3}&{\left( 2 \right)}\end{array}} \right.$

$\left( 2 \right) \Leftrightarrow \tan x.\dfrac{{\tan \dfrac{{2\pi }}{3} - \tan x}}{{1 + \tan \dfrac{{2\pi }}{3}.\tan x}} = 3$ 

$\Leftrightarrow \tan x.\dfrac{{ - \sqrt 3  - \tan x}}{{1 - \sqrt 3 \tan x}} = 3$ $\Rightarrow  - \sqrt 3 \tan x - {\tan ^2}x = 3 - 3\sqrt 3 \tan x$

$\Leftrightarrow {\tan ^2}x - 2\sqrt 3 \tan x + 3 = 0$

Đặt $\tan x = t$, phương trình trở thành

$\begin{array}{l}{t^2} - 2\sqrt 3 t + 3 = 0 \Leftrightarrow {\left( {t - \sqrt 3 } \right)^2} = 0\\ \Leftrightarrow t = \sqrt 3 \end{array}$

$\Leftrightarrow \tan x = \sqrt 3  \Leftrightarrow x = \dfrac{\pi }{3} + k\pi$

Từ $\left( 1 \right) \Leftrightarrow y = \dfrac{\pi }{3} - k\pi$.

${\cos ^2}x - 4\cos x + 3 = 0$

Đặt $\cos x = t\,\,\left( { - 1 \le t \le 1} \right)$ khi đó phương trình có dạng:

${t^2} - 4t + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\,\,\left( {ktm} \right)\\t = 1\,\,\,\left( {tm} \right)\end{array} \right.$

Khi $t = 1 \Leftrightarrow \cos x = 1 \Leftrightarrow x = k2\pi \,\,\left( {k \in Z} \right)$

${\sin ^2}x + 2\left( {m + 1} \right)\sin x - 3m\left( {m - 2} \right) = 0\,\,\,\left( * \right)$

Đặt $\sin x = t\,\,\left( { - 1 \le t \le 1} \right)$ khi đó phương trình có dạng ${t^2} + 2\left( {m + 1} \right)t - 3m\left( {m - 2} \right) = 0\,\,\,\left( 1 \right)$

Ta có: $\Delta ' = {\left( {m + 1} \right)^2} + 3m\left( {m - 2} \right) = 4{m^2} - 4m + 1 = {\left( {2m - 1} \right)^2} \ge 0\,\,\forall m \in R$

TH1: $\Delta ' = 0 \Leftrightarrow m = \dfrac{1}{2}$ phương trình (1) có nghiệm  $t =  - m - 1 = \dfrac{{ - 1}}{2} - 1 =  - \dfrac{3}{2}\,\,\left( {ktm} \right)$

TH2: $\Delta ' > 0 \Leftrightarrow m \ne \dfrac{1}{2}$. Khi đó phương trình có 2 nghiệm

$\left[ \begin{array}{l}{t_1} =  - m - 1 + 2m - 1 = m - 2\\{t_2} =  - m - 1 - 2m + 1 =  - 3m\end{array} \right.$

Để phương trình (*) có nghiệm thì phương trình (1) có nghiệm $- 1 \le t \le 1$

$\Leftrightarrow \left[ \begin{array}{l} - 1 \le m - 2 \le 1\\ - 1 \le  - 3m \le 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}1 \le m \le 3\\ - \dfrac{1}{3} \le m \le \dfrac{1}{3}\end{array} \right.$

Bước 1:

${\rm{cos}}2x - \left( {2m - 1} \right)\cos x - m + 1 = 0{\rm{ }}\left( 1 \right)$

$\Leftrightarrow 2\cos^2 x - \left( {2m - 1} \right)\cos x - m = 0$

Đặt $\cos x=t$

Phương trình trên trở thành:

$2t^2-(2m-1)t-m=0$

$(2t^2-2mt)+(t-m)=0$

$\Leftrightarrow \left[ \begin{array}{l}t=  - \dfrac{1}{2}\\t = m\end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}\cos x =  - \dfrac{1}{2}\\\cos x = m\end{array} \right..$

Bước 2:

Vì $x \in \left[ { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right]$ nên  $0 \le \cos x \le 1$.

Do đó $\cos x =  - \dfrac{1}{2}$ (loại).

Vậy phương trình (1) có đúng 2 nghiệm $x \in \left[ { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right]$ khi và chỉ khi $0 \le \cos x < 1$

$\Leftrightarrow 0 \le m < 1$.

(Nếu $\cos x=1$ thì có đúng 1 nghiệm $x=0$ $=>\cos x < 1$)

Bước 1:

$\cos 2x - 3\cos x = 4 \cos ^2\dfrac{x}{2}$$\Leftrightarrow 2{\cos ^2}x - 1 - 3\cos x = 2\left( {1 + \cos x} \right)$$\Leftrightarrow 2{\cos ^2}x - 5\cos x - 3 = 0$

Đặt $\cos x = t\,\,\left( { - 1 \le t \le 1} \right)$ khi đó phương trình có dạng $2{t^2} - 5t - 3 = 0$

Bước 2:

$\Leftrightarrow \left[ \begin{array}{l}t =  - \dfrac{1}{2}\,\,\,\,\left( {tm} \right)\\t = 3>1\,\,\left( {ktm} \right)\end{array} \right.$

$t =  - \dfrac{1}{2} \Leftrightarrow \cos x =  - \dfrac{1}{2}$$\Leftrightarrow \cos x =  \cos \dfrac{{2\pi }}{3}$

$\Leftrightarrow x =  \pm \dfrac{{2\pi }}{3} + k2\pi \,\,\,\left( {k \in Z} \right)$

Bước 1:

$\begin{array}{l}2{\sin ^2}x - 3\sin x + 1 = 0\\ \Leftrightarrow 2{\sin ^2}x - 2\sin x -\sin x+ 1 = 0\\\Leftrightarrow (\sin x-1)(2\sin x-1)=0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi }\\{\sin x = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \pi  - \dfrac{\pi }{6} + k2\pi  = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.}\end{array}} \right.\end{array}$

Bước 2:

Với $x = \dfrac{\pi }{2} + k2\pi$ thì $0 \le x < \dfrac{\pi }{2} \Rightarrow 0 \le \dfrac{\pi }{2} + k2\pi  < \dfrac{\pi }{2}$  vô nghiệm.

Với $x = \dfrac{\pi }{6} + k2\pi$ thì $0 \le x < \dfrac{\pi }{2} \Rightarrow 0 \le \dfrac{\pi }{6} + k2\pi  < \dfrac{\pi }{2}$$\Rightarrow k = 0 \Rightarrow x = \dfrac{\pi }{6}$.

Với $x = \dfrac{{5\pi }}{6} + k2\pi$ thì $0 \le x < \dfrac{\pi }{2} \Rightarrow 0 \le \dfrac{{5\pi }}{6} + k2\pi  < \dfrac{\pi }{2}$  vô nghiệm.

Vậy $x = \dfrac{\pi }{6}$.

Phương trình có nghiệm $\Leftrightarrow {m^2} + 25 \ge {\left( {m + 1} \right)^2} \Leftrightarrow 2m \le 24 \Leftrightarrow m \le 12$.

$\begin{array}{l}\,\,\,\,\,\,\sqrt 3 \cos 3x + \sin 3x = \sqrt 2 \\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\cos 3x + \dfrac{1}{2}\sin 3x = \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin 3x.\cos \dfrac{\pi }{3} + \cos 3x.\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {3x + \dfrac{\pi }{3}} \right) = \sin \left( {\dfrac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}3x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\3x + \dfrac{\pi }{3} = \dfrac{{3\pi }}{4} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}3x =  - \dfrac{\pi }{{12}} + k2\pi \\3x = \dfrac{{5\pi }}{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{{36}} + \dfrac{{k2\pi }}{3}\\x = \dfrac{{5\pi }}{{36}} + \dfrac{{k2\pi }}{3}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Bước 1:

$\begin{array}{l}\,\,\,\,\,\,\sqrt 3 \sin 4x - \cos 4x = \sin x - \sqrt 3 \cos x\\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\sin 4x - \dfrac{1}{2}\cos 4x = \dfrac{1}{2}\sin x - \dfrac{{\sqrt 3 }}{2}\cos x\\ \Leftrightarrow \sin 4x\cos \dfrac{\pi }{6} - \cos 4x\sin \dfrac{\pi }{6} = \sin x\sin \dfrac{\pi }{6} - \cos x\cos \dfrac{\pi }{6}\\ \Leftrightarrow \sin \left( {4x - \dfrac{\pi }{6}} \right) =  - \cos \left( {x + \dfrac{\pi }{6}} \right)\end{array}$

Bước 2:

$\Leftrightarrow \sin \left( {4x - \dfrac{\pi }{6}} \right) = \sin \left( {x - \dfrac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}4x - \dfrac{\pi }{6} = x - \dfrac{\pi }{3} + k2\pi \\4x - \dfrac{\pi }{6} = \dfrac{{4\pi }}{3} - x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x =  - \dfrac{\pi }{6} + k2\pi \\5x = \dfrac{{3\pi }}{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\\x = \dfrac{{3\pi }}{{10}} + \dfrac{{k2\pi }}{5}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)$

Bước 1:

$\begin{array}{l}\cos 7x\cos 5x - \sqrt 3 \sin 2x = 1 - \sin 7x\sin 5x\\ \Leftrightarrow \cos 7x\cos 5x + \sin 7x\sin 5x - \sqrt 3 \sin 2x = 1\\ \Leftrightarrow \cos \left( {7x - 5x} \right) - \sqrt 3 \sin 2x = 1\\ \Leftrightarrow \cos 2x - \sqrt 3 \sin 2x = 1\end{array}$

Bước 2:

$\Leftrightarrow \dfrac{1}{2}\cos 2x - \dfrac{{\sqrt 3 }}{2}\sin 2x = \dfrac{1}{2}\\ \Leftrightarrow \cos 2x\cos \dfrac{\pi }{3} - \sin 2x\sin \dfrac{\pi }{3} = \cos \dfrac{\pi }{3}\\ \Leftrightarrow \cos \left( {2x + \dfrac{\pi }{3}} \right) = \cos \dfrac{\pi }{3}$

Bước 3:

$\Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{3} = \dfrac{\pi }{3} + k2\pi \\2x + \dfrac{\pi }{3} =  - \dfrac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x =  - \dfrac{\pi }{3} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$

$\begin{array}{l}\,\,\,\,\,\,3\sin 2x + 4\cos 2x + 5\cos 2017x = 0\\ \Leftrightarrow \dfrac{3}{5}\sin 2x + \dfrac{4}{5}\cos 2x + \cos 2017x = 0\end{array}$

Đặt $\dfrac{3}{5} = sin\alpha  \Rightarrow \dfrac{4}{5} = \cos \alpha$, khi đó ta có:

$\begin{array}{l}\sin 2x\sin \alpha  + \cos 2x\cos \alpha  =  - \cos 2017x\\ \Leftrightarrow \cos \left( {2x - \alpha } \right) = \cos \left( {\pi  - 2017x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x - \alpha  = \pi  - 2017x + k2\pi \\2x - \alpha  =  - \pi  + 2017x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2019x = \pi  + \alpha  + k2\pi \\ - 2015x =  - \pi  + \alpha  + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{\pi  + \alpha }}{{2019}} + \dfrac{{k2\pi }}{{2019}}\\x = \dfrac{{\pi  - \alpha }}{{2015}} - \dfrac{{k2\pi }}{{2015}}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Bước 1:

$\begin{array}{l}\,\,\,\,\,\,3\sin 3x + \sqrt 3 \cos 9x = 1 + 4{\sin ^3}3x\\ \Leftrightarrow (3\sin 3x - 4{\sin ^3}3x )+ \sqrt 3 \cos 9x - 1 = 0\\ \Leftrightarrow \sin 9x + \sqrt 3 \cos 9x = 1\end{array}$

Bước 2:

$\Leftrightarrow \dfrac{1}{2}\sin 9x + \dfrac{{\sqrt 3 }}{2}\cos 9x = \dfrac{1}{2}$

$\Leftrightarrow \sin 9x\cos \dfrac{\pi }{3} + \cos 9x\sin \dfrac{\pi }{3} = \dfrac{1}{2}$

$\Leftrightarrow \sin \left( {9x + \dfrac{\pi }{3}} \right) = \sin \left( {\dfrac{\pi }{6}} \right)$

Bước 3:

$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}9x + \dfrac{\pi }{3} = \dfrac{\pi }{6} + k2\pi \\9x + \dfrac{\pi }{3} = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{{54}} + \dfrac{{k2\pi }}{9}\\x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{9}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

Bước 1:

ĐK:

$\begin{array}{l}\,\,\,\,\,\,\cos x + \sqrt 3 \sin x + 1 \ne 0\\ \Leftrightarrow 2\left( {\dfrac{{\sqrt 3 }}{2}\sin x + \dfrac{1}{2}\cos x} \right) \ne  - 1\\ \Leftrightarrow 2\left( {\sin x\cos \dfrac{\pi }{6} + \cos x\sin \dfrac{\pi }{6}} \right) \ne  - 1\\\, \Leftrightarrow 2\sin \left( {x + \dfrac{\pi }{6}} \right) \ne  - 1\\ \Leftrightarrow \sin \left( {x + \dfrac{\pi }{6}} \right) \ne  - \dfrac{1}{2} = \sin \left( {\dfrac{{ - \pi }}{6}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x + \dfrac{\pi }{6} \ne \dfrac{{ - \pi }}{6} + k2\pi \\x + \dfrac{\pi }{6} \ne \pi  - \dfrac{{ - \pi }}{6} + k2\pi \end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{{ - \pi }}{3} + k2\pi \\x \ne \pi  + k2\pi \end{array} \right.\end{array}$

Bước 2:

Đặt $t = \cos x + \sqrt 3 \sin x$$= 2\left( {\dfrac{{\sqrt 3 }}{2}\sin x + \dfrac{1}{2}\cos x} \right)$$= 2\left( {\sin x\cos \dfrac{\pi }{6} + \cos x\sin \dfrac{\pi }{6}} \right)$$= 2\sin \left( {x + \dfrac{\pi }{6}} \right) \in \left[ { - 2;2} \right]\backslash \left\{ { - 1} \right\}$

Bước 3:

Khi đó phương trình đã cho

$\begin{array}{l} \Leftrightarrow t = 3 - \dfrac{3}{{t + 1}} \Leftrightarrow t = \dfrac{{3t + 3}}{{t + 1}} - \dfrac{3}{{t + 1}}\\ \Leftrightarrow {t^2} + t = 3t + 3 - 3 \Leftrightarrow {t^2} - 2t = 0 \\\Leftrightarrow \left[ \begin{array}{l}t = 0\,\,\left( {tm} \right)\\t = 2\,\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Bước 4:

$\Leftrightarrow \left[ \begin{array}{l}2\sin \left( {x + \dfrac{\pi }{6}} \right) = 0\\2\sin \left( {x + \dfrac{\pi }{6}} \right) = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin \left( {x + \dfrac{\pi }{6}} \right) = 0\\\sin \left( {x + \dfrac{\pi }{6}} \right) = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{6} = k\pi \\x + \dfrac{\pi }{6} = \dfrac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{6} + k\pi \\x = \dfrac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{5\pi }}{6} + k\pi \\x = \dfrac{\pi }{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)$

Trường hợp 1: $\cos 2x = 0 \Leftrightarrow 2x = \dfrac{\pi }{2} + k\pi  \Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\,\,\left( {k \in Z} \right)$. Khi đó ${\sin ^2}2x = 1$

Thay vào phương trình ta có: $3.1 - 0 - 4.0 = 2 \Leftrightarrow 3 = 2$ (Vô lý)

$\Rightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\,\,\left( {k \in Z} \right)$ không là nghiệm của phương trình.

Trường hợp 2: $\cos 2x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\,\,\left( {k \in Z} \right)$.

Chia cả 2 vế của phương trình cho ${\cos ^2}2x$ ta được:

$3\dfrac{{{{\sin }^2}2x}}{{{{\cos }^2}2x}} - \dfrac{{\sin 2x}}{{\cos 2x}} - 4 = \dfrac{2}{{{{\cos }^2}2x}}$$\Leftrightarrow 3{\tan ^2}2x - \tan 2x - 4 = 2\left( {1 + {{\tan }^2}2x} \right)$$\Leftrightarrow {\tan ^2}2x - \tan 2x - 6 = 0$

Đặt $\tan 2x = t$. Khi đó phương trình trở thành

${t^2} - t - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t =  - 2\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}\tan 2x = 3\\\tan 2x =  - 2\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}2x = \arctan 3 + k\pi \\2x = \arctan \left( { - 2} \right) + k\pi \end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\arctan 3 + \dfrac{{k\pi }}{2}\\x = \dfrac{1}{2}\arctan \left( { - 2} \right) + \dfrac{{k\pi }}{2}\end{array} \right.\,\,\,\left( {k \in Z} \right)$