Một số phương trình lượng giác thường gặp

$4{\sin ^2}\dfrac{x}{2} - 3\sin x + 2 = 0 \Leftrightarrow 4{\sin ^2}\dfrac{x}{2} - 6\sin \dfrac{x}{2}\cos \dfrac{x}{2} + 2 = 0$

Trường hợp 1: $\cos \dfrac{x}{2} = 0 \Leftrightarrow \dfrac{x}{2} = \dfrac{\pi }{2} + k\pi  \Leftrightarrow x = \pi  + k2\pi \,\,\left( {k \in Z} \right)$. Khi đó ${\sin ^2}\dfrac{x}{2} = 1$

Thay vào phương trình ta có: $4.1 - 2.0 + 2 = 0 \Leftrightarrow 6 = 0\,\,\,\left( {Vô lý } \right)$

$\Rightarrow x = \pi  + k2\pi \,\,\left( {k \in Z} \right)$ không là nghiệm của phương trình.

Trường hợp 2: $\cos \dfrac{x}{2} \ne 0 \Leftrightarrow x \ne \pi  + k2\pi \,\,\left( {k \in Z} \right)$.

Chia cả 2 vế của phương trình (*) cho ${\cos ^2}\dfrac{x}{2}$ ta được:

$\begin{array}{l}4\dfrac{{{{\sin }^2}\dfrac{x}{2}}}{{{{\cos }^2}\dfrac{x}{2}}} - 6\dfrac{{\sin \dfrac{x}{2}}}{{\cos \dfrac{x}{2}}} + \dfrac{2}{{{{\cos }^2}\dfrac{x}{2}}} = 0\\ \Leftrightarrow 4{\tan ^2}\dfrac{x}{2} - 6\tan \dfrac{x}{2} + 2\left( {1 + {{\tan }^2}\dfrac{x}{2}} \right) = 0\\ \Leftrightarrow 6{\tan ^2}\dfrac{x}{2} - 6\tan \dfrac{x}{2} + 2 = 0\\ \Leftrightarrow 3{\tan ^2}\dfrac{x}{2} - 3\tan \dfrac{x}{2} + 1 = 0\end{array}$

Đặt $\tan \dfrac{x}{2} = t$ khi đó phương trình có dạng: $3{t^2} - 3t + 1 = 0$

Ta có: $\Delta  = {3^2} - 4.3 =  - 3 < 0 \Rightarrow$ phương trình vô nghiệm.

Trường hợp 1: $\cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)$. Khi đó ${\sin ^2}x = 1$

Thay vào phương trình ta có: $2\sqrt 3 .0 + 6.0 = 3 + \sqrt 3$(Vô lý)

$\Rightarrow x = \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)$ không là nghiệm của phương trình.

Trường hợp 2: $\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)$. Chia cả 2 vế của phương trình cho ${\cos ^2}x$ ta được:

$\begin{array}{l}2\sqrt 3  + 6\dfrac{{\sin x}}{{\cos x}} = \dfrac{{3 + \sqrt 3 }}{{{{\cos }^2}x}}\\ \Leftrightarrow 2\sqrt 3  + 6\tan x = \left( {3 + \sqrt 3 } \right)\left( {1 + {{\tan }^2}x} \right)\\ \Leftrightarrow \left( {3 + \sqrt 3 } \right){\tan ^2}x - 6\tan x + 3 - \sqrt 3  = 0\end{array}$

Đặt $\tan x = t$ khi đó phương trình có dạng

$\left( {3 + \sqrt 3 } \right){t^2} - 6t + 3 - \sqrt 3  = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = 2 - \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x = 2 - \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = \arctan \left( {2 - \sqrt 3 } \right) + k\pi \end{array} \right.\,\,\left( {k \in Z} \right)$

Vậy phương trình có 2 họ nghiệm.

ĐK: $\cos x \ne 0.$

$\dfrac{1}{2}\cos 4x + \dfrac{{4\tan x}}{{1 + {{\tan }^2}x}} = m$$\Leftrightarrow \dfrac{1}{2}\cos 4x + \dfrac{{4\tan x}}{{\dfrac{1}{{{{\cos }^2}x}}}} = m$$\Leftrightarrow \dfrac{1}{2}\cos 4x + 4\sin x\cos x = m$

$\Leftrightarrow \dfrac{1}{2}\left( {1 - 2{{\sin }^2}2x} \right) + 2\sin 2x = m$$\Leftrightarrow {\sin ^2}2x - 2\sin 2x + m - \dfrac{1}{2} = 0$

Đặt $\sin 2x = t\,\left( {t \in \left[ { - 1;1} \right]} \right)$. Khi đó phương trình trở thành: ${t^2} - 2t + m - \dfrac{1}{2} = 0\,(*)$

Phương trình đã cho vô nghiệm $\Leftrightarrow \left( * \right)$ không có nghiệm thuộc $\left[ { - 1;1} \right]$.

Xét hàm $f\left( t \right) = {t^2} - 2t$ có bảng biến thiên:

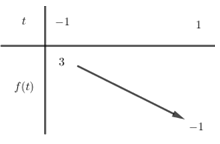
Từ bảng biến thiên ta thấy, phương trình $\left( * \right)$ không có nghiệm thuộc $\left[ { - 1;1} \right]$ nếu và chỉ nếu đường thẳng $y = \dfrac{1}{2} - m$ không cắt đồ thị hàm số $y = f\left( t \right)$ trong đoạn $\left[ { - 1;1} \right]$

$\Leftrightarrow \left[ \begin{array}{l}\dfrac{1}{2} - m > 3\\\dfrac{1}{2} - m <  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m <  - \dfrac{5}{2}\\m > \dfrac{3}{2}\end{array} \right.$.

Đặt $|\sin x + \cos x| = t\,\left( {t \in \left[ {0 ;\sqrt 2 } \right]} \right) \Rightarrow \sin 2x = {t^2} - 1$. Khi đó phương trình trở thành:

$2{t^2} - 3\sqrt 6 t + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \sqrt 6 \,(L)\\t = \dfrac{{\sqrt 6 }}{2}\,(TM)\end{array} \right. \Rightarrow \left| {\sin x + \cos x} \right| = \dfrac{{\sqrt 6 }}{2} \Leftrightarrow \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right) =  \pm \dfrac{{\sqrt 6 }}{2}$

$\Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) =  \pm \dfrac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = \sin \left( { \pm \dfrac{\pi }{3}} \right) \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{4} = \dfrac{\pi }{3} + k2\pi \\x + \dfrac{\pi }{4} = \dfrac{{2\pi }}{3} + k2\pi \\x + \dfrac{\pi }{4} =  - \dfrac{\pi }{3} + k2\pi \\x + \dfrac{\pi }{4} = \dfrac{{4\pi }}{3} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{5\pi }}{{12}} + k2\pi \\x =  - \dfrac{{7\pi }}{{12}} + k2\pi \\x = \dfrac{{13\pi }}{{12}} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{5\pi }}{{12}} + k2\pi \\x =  - \dfrac{{7\pi }}{{12}} + k2\pi \\x = \dfrac{{13\pi }}{{12}} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{{5\pi }}{{12}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).$

Ta có:

${\sin ^4}x + {\cos ^4}x$$= {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x$$= 1 - \dfrac{1}{2}{\sin ^2}2x$$= \dfrac{3}{4} + \dfrac{1}{4}\cos 4x$

${\sin ^6}x + {\cos ^6}x$$= {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^3}$$- 3{\sin ^2}x{\cos ^2}x\left( {{{\sin }^2}x + {{\cos }^2}x} \right)$$= 1 - \dfrac{3}{4}{\sin ^2}2x$$= \dfrac{5}{8} + \dfrac{3}{8}\cos 4x$

Phương trình đã cho trở thành

$4\left( {\dfrac{3}{4} + \dfrac{1}{4}\cos 4x} \right) - 8\left( {\dfrac{5}{8} + \dfrac{3}{8}\cos 4x} \right) - 4{\sin ^2}4x = m$

$\Leftrightarrow 3 + \cos 4x - 5 - 3\cos 4x - 4\left( {1 - {{\cos }^2}4x} \right) = m$

$\Leftrightarrow 4{\cos ^2}4x - 2\cos 4x = m + 6$

Đặt $t = \cos 4x,t \in \left[ { - 1;1} \right]$, phương trình trở thành $4{t^2} - 2t = m + 6\,\,\left( * \right)$

Phương trình đã cho vô nghiệm $\Leftrightarrow \left( * \right)$ không có nghiệm thuộc đoạn $\left[ { - 1;1} \right]$.

Xét hàm $f\left( t \right) = 4{t^2} - 2t$ trong đoạn $\left[ { - 1;1} \right]$ có:

Đồ thị của $f\left( t \right)$ là parabol có hoành độ đỉnh $t = \dfrac{1}{4} \in \left[ { - 1;1} \right]$.

Bảng biến thiên:

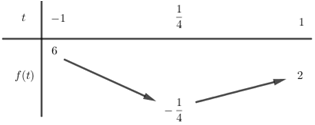
Phương trình $\left( * \right)$ không có nghiệm thuộc $\left[ { - 1;1} \right]$$\Leftrightarrow$$\left[ \begin{array}{l}m + 6 <  - \dfrac{1}{4}\\m + 6 > 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m <  - \dfrac{{25}}{4}\\m > 0\end{array} \right.$.

Vậy $m <  - \dfrac{{25}}{4}$ hoặc $m > 0$.

$\begin{array}{l}\sin 2x + 3\sin 4x = 0 \Leftrightarrow \sin 2x + 6\sin 2x\cos 2x = 0\\ \Leftrightarrow \sin 2x\left( {1 + 6\cos 2x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\1 + 6\cos 2x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\\cos 2x =  - \dfrac{1}{6}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2x = k\pi \\2x =  \pm \arccos \left( { - \dfrac{1}{6}} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{2}\\x =  \pm \dfrac{1}{2}\arccos \left( { - \dfrac{1}{6}} \right) + k\pi \end{array} \right.\left( {k \in Z} \right)\end{array}$

Bước 1:

Điều kiện:

$1 - \sin 2x \ne 0 \Leftrightarrow \sin 2x \ne 1 \Leftrightarrow 2x \ne \dfrac{\pi }{2} + k2\pi  \Leftrightarrow x \ne \dfrac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)$

Bước 2:

$\dfrac{{\cos 2x}}{{1 - \sin 2x}} = 0 \Leftrightarrow \cos 2x = 0 \Leftrightarrow {\cos ^2}2x = 0$

$\Leftrightarrow {1-{\sin ^2}2x = 0} \Leftrightarrow {\sin ^2}2x = 1$$\Leftrightarrow \sin 2x =  - 1$ (vì $\sin 2x \ne 1$)

$\Leftrightarrow 2x =  - \dfrac{\pi }{2} + k2\pi  \Leftrightarrow x =  - \dfrac{\pi }{4} + k\pi$

Đặt $k=l+1$ ta được:

$- \dfrac{\pi }{4} + k\pi=  - \dfrac{\pi }{4} + l\pi+\pi$$= \dfrac{{3\pi }}{4} + l\pi \left( {l \in Z} \right)$

Vậy $x= \dfrac{{3\pi }}{4} + l\pi \left( {l \in Z} \right)$ hay  $x= \dfrac{{3\pi }}{4} + k\pi \left( {l \in Z} \right)$

$\left\{ \begin{array}{l}1 - {\tan ^2}x \ne 0\\\cos 2x \ne 0\\\cos x \ne 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}\dfrac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cos }^2}x}} \ne 0\\\cos 2x \ne 0\\\cos x \ne 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}\cos 2x \ne 0\\\cos x \ne 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}2x \ne \dfrac{\pi }{2} + k\pi \\x \ne \dfrac{\pi }{2} + k\pi \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\\x \ne \dfrac{\pi }{2} + k\pi \end{array} \right.\,\,\,\left( {k \in Z} \right)$

$\begin{array}{l}\dfrac{{{a^2}}}{{1 - {{\tan }^2}x}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}} \Leftrightarrow \dfrac{{{a^2}}}{{\dfrac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cos }^2}x}}}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}}\\ \Leftrightarrow \dfrac{{{a^2}{{\cos }^2}x}}{{\cos 2x}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}} \Leftrightarrow {a^2}{\cos ^2}x = {\sin ^2}x + {a^2} - 2\\ \Leftrightarrow {a^2}{\cos ^2}x = 1 - {\cos ^2}x + {a^2} - 2\\ \Leftrightarrow \left( {{a^2} + 1} \right){\cos ^2}x = {a^2} - 1 \Leftrightarrow {\cos ^2}x = \dfrac{{{a^2} - 1}}{{{a^2} + 1}} < 1\end{array}$

Vì  $\cos x \ne 0 \Rightarrow 0 < {\cos ^2}x \le 1 \Leftrightarrow {\cos ^2}x > 0 \Leftrightarrow {a^2} - 1 > 0 \Rightarrow \left| a \right| > 1$

Bước 1:

$\left\{ \begin{array}{l}x - y = \dfrac{\pi }{3}\\\cos x - \cos y =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y + \dfrac{\pi }{3}\\\cos \left( {y + \dfrac{\pi }{3}} \right) - \cos y =  - 1\left( * \right)\end{array} \right.$

Bước 2:

$\begin{array}{l}\left( * \right) \Leftrightarrow  - 2\sin \left( {y + \dfrac{\pi }{6}} \right).\sin \dfrac{\pi }{6} =  - 1\\ \Leftrightarrow  - 2\sin \left( {y + \dfrac{\pi }{6}} \right).\dfrac{1}{2} =  - 1\\ \Leftrightarrow \sin \left( {y + \dfrac{\pi }{6}} \right) = 1\end{array}$

Bước 3:

$\Leftrightarrow y + \dfrac{\pi }{6} = \dfrac{\pi }{2} + k2\pi  \Leftrightarrow y = \dfrac{\pi }{3} + k2\pi \left( {k \in Z} \right)$$\Rightarrow x = y + \dfrac{\pi }{3} = \dfrac{{2\pi }}{3} + k2\pi \left( {k \in Z} \right)$

Vậy nghiệm của hệ phương trình là: $\left( {x;y} \right) = \left( {\dfrac{{2\pi }}{3} + k2\pi ;\dfrac{\pi }{3} + k2\pi } \right)\,\,\,\left( {k \in Z} \right)$

ĐK: $\sin x \ne 0 \Leftrightarrow x \ne k\pi \,\,\left( {k \in Z} \right)$

$\sqrt 3 {\cot ^2}x - 4\cot x + \sqrt 3  = 0$

Đặt $\cot x = t$ khi đó phương trình có dạng

$\sqrt 3 {t^2} - 4t + \sqrt 3  = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{1}{{\sqrt 3 }}\\t = \sqrt 3 \end{array} \right. \Rightarrow \left[ \begin{array}{l}\cot x = \dfrac{1}{{\sqrt 3 }}\\\cot x = \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{3} + k\pi \\x = \dfrac{\pi }{6} + k\pi \end{array} \right.\,\,\left( {k \in Z} \right)\,\,\left( {tm} \right)$

Khi $m = 1$ phương trình có dạng: ${\sin ^2}3x - 2\sin 3x - 3 = 0$

Đặt $\sin 3x = t\,\,\left( { - 1 \le t \le 1} \right)$ khi đó phương trình có dạng ${t^2} - 2t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t =  - 1\,\,\left( {tm} \right)\\t = 3\,\,\,\,\,\left( {ktm} \right)\end{array} \right.$

$t =  - 1 \Leftrightarrow \sin 3x =  - 1 \Leftrightarrow 3x =  - \dfrac{\pi }{2} + k2\pi  \Leftrightarrow x =  - \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3}\,\,\,\left( {k \in Z} \right)$

Bước 1:

$\begin{array}{l}4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\\  \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 8.\dfrac{{1 + \cos 2x}}{2} - 9 = 0\\ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4\left( {1 + \cos 2x} \right) - 9 = 0\\\Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4 + 4\cos 2x - 9 = 0\\ \Leftrightarrow 4 - 4{\cos ^2}2x + 4\cos 2x - 5 = 0 \\\Leftrightarrow  - 4{\cos ^2}2x + 4\cos 2x - 1 = 0\end{array}$

Bước 2:

Đặt $\cos 2x = t\,\,\left( { - 1 \le t \le 1} \right)$ khi đó phương trình có dạng 

$- 4{t^2} + 4t - 1 = 0$$\Leftrightarrow - \left( {4{t^2} - 4t + 1} \right) = 0$$\Leftrightarrow  - {\left( {2t - 1} \right)^2} = 0$ $\Leftrightarrow t = \dfrac{1}{2}\left( {tm} \right)$

$\begin{array}{l} \Leftrightarrow \cos 2x = \dfrac{1}{2} \Leftrightarrow \cos 2x =\cos \dfrac{\pi }{3} \\\Leftrightarrow 2x =  \pm \dfrac{\pi }{3} + k2\pi \Leftrightarrow x =  \pm \dfrac{\pi }{6} + k\pi \left( {k \in Z} \right)\end{array}$

$4{\sin ^2}x - 4\sin x - 3 = 0$

Đặt $\sin x = t\,\,\left( { - 1 \le t \le 1} \right)$ khi đó phương trình có dạng: $4{t^2} - 4t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{3}{2}\,\,\,\,\,\,\left( {ktm} \right)\\t =  - \dfrac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right.$

$t =  - \dfrac{1}{2} \Leftrightarrow \sin x =  - \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.\,\,\,\left( {k \in Z} \right)$

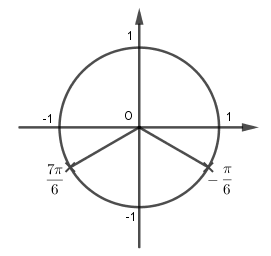
Vây số vị trí biểu diễn các nghiệm của phương trình $4{\sin ^2}x - 4\sin x - 3 = 0$ trên đường tròn lượng giác là 2 điểm như hình trên.

$\sqrt 3 \sin 2x - m\cos 2x = 1$

Ta có: $\left\{ \begin{array}{l}a = \sqrt 3 \\b =  - m\\c = 1\end{array} \right.$

Để phương trình có nghiệm thì ${a^2} + {b^2} \ge {c^2} \Leftrightarrow 3 + {m^2} \ge 1 \Leftrightarrow {m^2} \ge  - 2$ (luôn đúng với $\forall m$ )

Vậy phương trình luôn có nghiệm với mọi $m$.

$\begin{array}{l}\,\,\,\,\sqrt 3 \sin 2x - \cos 2x + 1 = 0\\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\sin 2x - \dfrac{1}{2}\cos 2x + \dfrac{1}{2} = 0\\ \Leftrightarrow \sin 2x.\cos \dfrac{\pi }{6} - \cos 2x.\sin \dfrac{\pi }{6} =  - \dfrac{1}{2}\\ \Leftrightarrow \sin \left( {2x - \dfrac{\pi }{6}} \right) = \sin \left( { - \dfrac{\pi }{6}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x - \dfrac{\pi }{6} =  - \dfrac{\pi }{6} + k2\pi \\2x - \dfrac{\pi }{6} = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2x = k2\pi \\2x = \dfrac{{4\pi }}{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \dfrac{{2\pi }}{3} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$

$\begin{array}{l}\,\,\,\,\,\,2\sqrt 2 \left( {\sin x + \cos x} \right)\cos x = 3 + \cos 2x\\ \Leftrightarrow 2\sqrt 2 \sin x\cos x + 2\sqrt 2 {\cos ^2}x = 3 + \cos 2x\\ \Leftrightarrow \sqrt 2 \sin 2x + \sqrt 2 \left( {1 + \cos 2x} \right) = 3 + \cos 2x\\ \Leftrightarrow \sqrt 2 \sin 2x + \left( {\sqrt 2  - 1} \right)\cos 2x = 3 - \sqrt 2 \end{array}$

Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}a = \sqrt 2 \\b = \sqrt 2  - 1\\c = 3 - \sqrt 2 \end{array} \right.\\ \Rightarrow {a^2} + {b^2} - {c^2} \\= 2 + {\left( {\sqrt 2  - 1} \right)^2} - {\left( {3 - \sqrt 2 } \right)^2} \\= 2 + 3 - 2\sqrt 2  - 11 + 6\sqrt 2  \\=  - 6 + 4\sqrt 2  < 0\\ \Rightarrow {a^2} + {b^2} < {c^2}\end{array}$

Vậy phương trình vô nghiệm

Bước 1:

${\mkern 1mu} \sin x + \sqrt 3 \cos x = \sqrt 2$$\Leftrightarrow \dfrac{1}{2}\sin x + \dfrac{{\sqrt 3 }}{2}\cos x = \dfrac{{\sqrt 2 }}{2}$

$\Leftrightarrow \sin x\cos \dfrac{\pi }{3} + \cos x\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 2 }}{2}$$\Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{4}$

Bước 2:

$\Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi }\\{x + \dfrac{\pi }{3} = \dfrac{{3\pi }}{4} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {\rm{\;}} - \dfrac{\pi }{{12}} + k2\pi }\\{x = \dfrac{{5\pi }}{{12}} + k2\pi }\end{array}} \right.\left( {k \in \mathbb{Z}} \right)$

$\Rightarrow \left\{ {\begin{array}{*{20}{l}}{\alpha {\rm{\;}} = {\rm{\;}} - \dfrac{\pi }{{12}}}\\{\beta {\rm{\;}} = \dfrac{{5\pi }}{{12}}}\end{array}} \right.$

(Vì $- \dfrac{\pi }{{12}}$ và $\dfrac{{5\pi }}{{12}}$ đều thỏa mãn điều kiện đề bài)

$\Rightarrow \alpha .\beta {\rm{\;}} = \dfrac{{ - 5{\pi ^2}}}{{144}}$

Bước 1:

Với $a = 1;b = \sqrt 3  - 2;c = 1$ ta có:

$\begin{array}{l}\sin x + \left( {\sqrt 3  - 2} \right)\cos x = 1\\ \Leftrightarrow \dfrac{1}{{\sqrt {8 - 4\sqrt 3 } }}\sin x + \dfrac{{\sqrt 3  - 2}}{{\sqrt {8 - 4\sqrt 3 } }}\cos x \\= \dfrac{1}{{\sqrt {8 - 4\sqrt 3 } }}\end{array}$

Đặt $\dfrac{1}{{\sqrt {8 - 4\sqrt 3 } }} = \cos \alpha  \Rightarrow \dfrac{{\sqrt 3  - 2}}{{\sqrt {8 - 4\sqrt 3 } }} = \sin \alpha$. Khi đó phương trình tương đương:

$\sin x\cos \alpha  + \cos x\sin \alpha  = \cos \alpha$

Bước 2:

$\begin{array}{l} \Leftrightarrow \sin \left( {x + \alpha } \right) = \sin \left( {\dfrac{\pi }{2} - \alpha } \right)\\ \Leftrightarrow \left[ \begin{array}{l}x + \alpha  = \dfrac{\pi }{2} - \alpha  + k2\pi \\x + \alpha  = \dfrac{\pi }{2} + \alpha  + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} - 2\alpha  + k2\pi \\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.\end{array}$

Vì $\alpha  \ne 0 \Rightarrow$ có 2 vị trí biểu diễn nghiệm của phương trình.

$\begin{array}{l}2\sqrt 3 {\cos ^2}\dfrac{{5x}}{2} + \sin 5x = 1 + \sqrt 3  \Leftrightarrow \sqrt 3 \left( {1 + \cos 5x} \right) + \sin 5x = 1 + \sqrt 3 \\ \Leftrightarrow \sin 5x + \sqrt 3 \cos 5x = 1 \Leftrightarrow \dfrac{1}{2}\sin 5x + \dfrac{{\sqrt 3 }}{2}\cos 5x = \dfrac{1}{2}\\ \Leftrightarrow \sin 5x\cos \dfrac{\pi }{3} + \cos 5x\sin \dfrac{\pi }{3} = \dfrac{1}{2} \Leftrightarrow \sin \left( {5x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{6}\\ \Leftrightarrow \left[ \begin{array}{l}5x + \dfrac{\pi }{3} = \dfrac{\pi }{6} + k2\pi \\5x + \dfrac{\pi }{3} = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{{30}} + \dfrac{{k2\pi }}{5}\\x = \dfrac{\pi }{{10}} + \dfrac{{k2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Với họ nghiệm $x =  - \dfrac{\pi }{{30}} + \dfrac{{k2\pi }}{5}\,\,\left( {k \in \mathbb{Z}} \right)$, ta được

$\begin{array}{l}0 \le  - \dfrac{\pi }{{30}} + \dfrac{{k2\pi }}{5}\,\, \le \dfrac{\pi }{2} \Leftrightarrow 0 \le  - \dfrac{1}{{30}} + \dfrac{{2k}}{5}\,\, \le \dfrac{1}{2} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{{12}} \le k \le \dfrac{4}{3}\\k \in \mathbb{Z}\end{array} \right. \Rightarrow k = 1\\ \Rightarrow x =  - \dfrac{\pi }{{30}} + \dfrac{{2\pi }}{5} = \dfrac{{11\pi }}{{30}}\end{array}$

Với họ nghiệm $x = \dfrac{\pi }{{10}} + \dfrac{{k2\pi }}{5}\,\,\left( {k \in \mathbb{Z}} \right)$, ta được:

$\begin{array}{l}0 \le \dfrac{\pi }{{10}} + \dfrac{{k2\pi }}{5}\,\,\, \le \dfrac{\pi }{2} \Leftrightarrow 0 \le \dfrac{1}{{10}} + \dfrac{{2k}}{5}\,\, \le \dfrac{1}{2} \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{1}{4} \le k \le 1\\k \in \mathbb{Z}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}k = 0\\k = 1\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}x = \dfrac{\pi }{{10}}\\x = \dfrac{\pi }{{10}} + \dfrac{{2\pi }}{5} = \dfrac{\pi }{2}\end{array} \right.\end{array}$

Vậy tổng các nghiệm thuộc đoạn $\left[ {0;\dfrac{\pi }{2}} \right]$ là: $\dfrac{{11\pi }}{{30}} + \dfrac{\pi }{{10}} + \dfrac{\pi }{2} = \dfrac{{29\pi }}{{30}}$

Bước 1:

$\begin{array}{l}{\sin ^3}x + {\cos ^3}x = \sin x - \cos x \\\Leftrightarrow  {\cos ^3}x + \cos x= \sin x -\sin ^3x  \\\Leftrightarrow \cos x\left( {{{\cos }^2}x + 1} \right) = \sin x\left( {1 - {{\sin }^2}x} \right)\\ \Leftrightarrow \cos x\left( {\dfrac{{1 + \cos 2x}}{2} + 1} \right) = \sin x.{\cos ^2}x\end{array}$

$\Leftrightarrow \cos x\left( {\dfrac{{1 + \cos 2x}}{2} + 1 - \sin x\cos x} \right) = 0$

$\begin{array}{l}\Leftrightarrow \cos x.\dfrac{{1 + \cos 2x +2- \sin 2x}}{2} = 0\end{array}$

$\Leftrightarrow \cos x\left( {1 + \cos 2x + 2 - \sin 2x} \right) = 0 \\\Leftrightarrow \cos x\left( { - \sin 2x + \cos 2x + 3} \right) = 0$

$\Leftrightarrow \left[ \begin{array}{l}\cos x = 0\left( 1 \right)\\ - \sin 2x + \cos 2x + 3 = 0\left( 2 \right)\end{array} \right.$

Bước 2:

$\left( 1 \right) \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$

Xét (2) ta có: $\left\{ \begin{array}{l}a =  - 1\\b = 1\\c =  - 3\end{array} \right. \Rightarrow {a^2} + {b^2} < {c^2}$

$\Rightarrow$ phương trình (2) vô nghiệm.

Vậy nghiệm của phương trình là:$x = \dfrac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)$