Có bao nhiêu giá trị nguyên dương của \(m\) để hàm số

\(y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\sin x + 2\sqrt 3 \cos x - m + 3} \) xác định với mọi\(x \in \mathbb{R}\)?

Bước 1:

\(\begin{array}{l}y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\sin x + 2\sqrt 3 \cos x - m + 3} \\y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\left( {\sin x - \sqrt 3 \cos x} \right) - m + 3} \end{array}\)

Bước 2:

 Đặt \(t = \sin x - \sqrt 3 \cos x = 2\left( {\dfrac{1}{2}\sin x - \dfrac{{\sqrt 3 }}{2}\cos x} \right)\)\( = 2\sin \left( {x - \dfrac{\pi }{3}} \right)\) \( \Rightarrow  - 2 \le t \le 2\).

Bước 3:

Khi đó hàm số trở thành \(y = \sqrt {{t^2} - 2t - m + 3} \,\,\forall t \in \left[ { - 2;2} \right]\,\,\left( * \right)\).

Để hàm số ban đầu xác định với mọi\(x \in \mathbb{R}\) thì hàm số xác định với mọi \(t \in \left[ { - 2;2} \right]\).

Tức là \({t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right]\).

Bước 4:

Xét hàm số \(f\left( t \right) = {t^2} - 2t - m + 3\) trên \(\left[ { - 2;2} \right]\) ta có BBT:

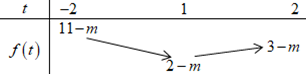
Để \({t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right]\) thì \(2 - m \ge 0 \Leftrightarrow m \le 2\).

Mà \(m\) nguyên dương \( \Rightarrow m \in \left\{ {1;2} \right\}\).