Tổng các nghiệm của phương trình \(2\cos 3x\left( {2\cos 2x + 1} \right) = 1\) trên đoạn \(\left[ { - 4\pi ;6\pi } \right]\) là:

Xét \(\sin x = 0 \Leftrightarrow x = m\pi \): Thay vào phương trình thấy không thỏa mãn

Xét \(\sin x \ne 0 \Leftrightarrow x \ne m\pi \)

\(2\cos 3x\left( {2\cos 2x + 1} \right) = 1\)

\( \Leftrightarrow 2\left[ {\cos 5x + \cos x} \right] + 2\cos 3x = 1\)

\( \Leftrightarrow 2\sin x\cos 5x + 2\sin x\cos 3x + 2\sin x\cos x = \sin x\)

\( \Leftrightarrow \left( {\sin 6x - \sin 4x} \right) + \left( {\sin 4x - \sin 2x} \right) + \sin 2x = \sin x\)

\( \Leftrightarrow \sin 6x = \sin x\)

\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = \dfrac{{k2\pi }}{5}\\x = \dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}\end{array} \right.\\x \ne m\pi \end{array} \right.{\rm{  }}\left( {k,l \in \mathbb{Z}} \right)\).

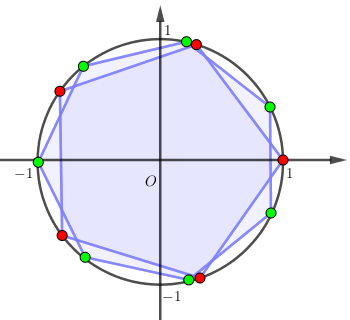
Biểu diễn các điểm của hai họ nghiệm \(x = \dfrac{{k2\pi }}{5}\) và \(x = \dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}\) trên đường tròn đơn vị ta thấy các điểm đều không trùng nhau. Do đó:

+) Với \(\left\{ \begin{array}{l}x = \dfrac{{k2\pi }}{5}\\x \ne m\pi \\x \in \left[ { - 4\pi ;6\pi } \right]\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}k \in \left\{ { - 10; - 9; - 8;...14;15} \right\}\\k \notin \left\{ { - 10; - 5;0;5,10,15} \right\}\end{array} \right.\)

\( \Rightarrow \)các giá trị \(x\) cần loại bỏ là \( - 4\pi ,\)\( - 2\pi ,\)\(0,\)\(2\pi ,\)\(4\pi ,\)\(6\pi \). Tổng các giá trị này là $6\pi $

Với \(\left\{ \begin{array}{l}x = \dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}\\x \ne m\pi \\x \in \left[ { - 4\pi ;6\pi } \right]\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}l \in \left\{ { - 14; - 13; - 12;...19;20} \right\}\\l \notin \left\{ { - 4; - 11;3;10;17} \right\}\end{array} \right.\)

\( \Rightarrow \)các giá trị \(x\) cần loại bỏ là \( - \pi ,\)\( - 3\pi ,\)\(\pi ,\)\(3\pi ,\)\(5\pi \). Tổng các giá trị này là $5\pi $

Vậy tổng nghiệm $S = \left[ {\sum\limits_{k =  - 10}^{15} {\left( {\dfrac{{k2\pi }}{5}} \right)}  - \left( {6\pi } \right)} \right] + \left[ {\sum\limits_{l =  - 14}^{20} {\left( {\dfrac{\pi }{7} + \dfrac{{l2\pi }}{7}} \right)}  - 5\pi } \right] = 50\pi $.