Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.MNPQ\) cạnh bằng \(a.\) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \((CNQ).\)
Trả lời bởi giáo viên
Đáp án đúng: a
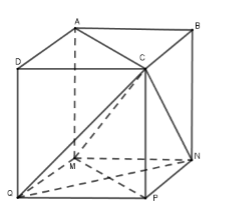
Gắn hệ trục tọa độ với \(M \equiv O;\,MN \equiv Ox;\,MA \equiv Oy;\,MQ \equiv Oz\)
Coi hình lập phương cạnh bằng \(1.\) Khi đó ta có \(M\left( {0;0;0} \right);\,N\left( {1;0;0} \right);A\left( {0;1;0} \right);Q\left( {0;0;1} \right);C\left( {1;1;1} \right)\)
Ta có \(\overrightarrow {NC} = \left( {0;1;1} \right);\,\overrightarrow {NQ} = \left( { - 1;0;1} \right) \Rightarrow \left[ {\overrightarrow {NC} ;\overrightarrow {NQ} } \right] = \left( {1; - 1;1} \right)\)
Mặt phẳng \(\left( {CNQ} \right)\) đi qua \(C;N;Q\) nên nhận \(\overrightarrow n = \left[ {\overrightarrow {NC} ;\overrightarrow {NQ} } \right] = \left( {1; - 1;1} \right)\) làm 1 VTPT.
Phương trình \(\left( {CNQ} \right):1\left( {x - 1} \right) - y + z = 0 \Leftrightarrow x - y + z - 1 = 0\)
Khoảng cách cần tìm là \(d\left( {A;\left( {CNQ} \right)} \right) = \dfrac{{\left| {0 - 1 + 0 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \dfrac{{2\sqrt 3 }}{3}\)
Hướng dẫn giải:
Gắn hệ trục tọa độ \(Oxyz\). Viết phương trình mặt phẳng \(\left( {CNQ} \right)\)
Đưa về tính khoảng cách từ điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) đến mặt phẳng \(\left( P \right):ax + by + cz + d = 0\)
\(d\left( {A;\left( P \right)} \right) = \dfrac{{\left| {a{x_A} + b{y_A} + c{z_A}} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
