Đề thi THPT QG 2019 – mã đề 104
Cho hình chóp \(Oxy\) có đáy là hình vuông cạnh \(a\), mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên).
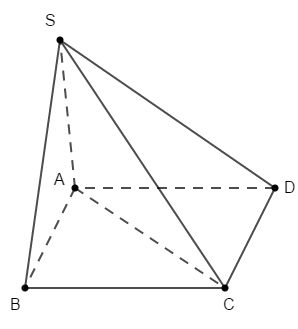
Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\) bằng
Trả lời bởi giáo viên
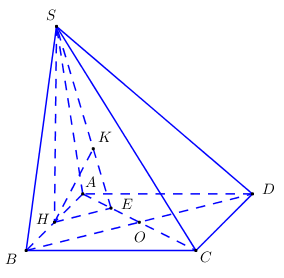
Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot AB\) (do tam giác \(SAB\) đều).
Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SH \bot AB\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\).
Ta có \(BH \cap \left( {SAC} \right) = A \Rightarrow \dfrac{{d\left( {B;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{BA}}{{HA}} = 2\) \( \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)\).
Gọi \(O = AC \cap BD\), gọi \(E\) là trung điểm của \(OA\).
Vì \(ABCD\) là hình vuông nên \(AC \bot BD\). Mà \(HE//OB \Rightarrow HE//BD\) (\(HE\) là đường trung bình của tam giác \(OAB\)) \( \Rightarrow HE \bot AC\).
Ta có \(\left\{ \begin{array}{l}AC \bot SH\,\,\left( {SH \bot \left( {ABCD} \right)} \right)\\AC \bot HE\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow AC \bot \left( {SHE} \right)\).
Trong \(\left( {SHE} \right)\) kẻ \(HK \bot SE\,\,\left( {K \in SE} \right)\) ta có \(\left\{ \begin{array}{l}HK \bot SE\\HK \bot AC\,\,\left( {AC \bot \left( {SHK} \right)} \right)\end{array} \right. \Rightarrow HK \bot \left( {SAC} \right)\).
Ta có \(HE = \dfrac{1}{2}OB = \dfrac{1}{4}BD = \dfrac{{a\sqrt 2 }}{4}\); \(SH = \dfrac{{a\sqrt 3 }}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SHE\) có: \(HK = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{4}.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {\dfrac{{2{a^2}}}{{16}} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{a\sqrt {21} }}{{14}}\).
Vậy \(d\left( {B;\left( {SAC} \right)} \right) = 2HK = \dfrac{{a\sqrt {21} }}{7}\).
Hướng dẫn giải:
- Gọi \(H\) là trung điểm của AB
- Sử dụng phương pháp đổi khoảng cách.
- Gọi \(O = AC \cap BD\), gọi \(E\) là trung điểm của \(OA\).
- Trong \(\left( {SHE} \right)\) kẻ \(HK \bot SE\,\,\left( {K \in SE} \right)\)

