Câu hỏi:
2 năm trước
Gọi \({\rm{E}}\) là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng DE và SC.
Trả lời bởi giáo viên
Đáp án đúng: b
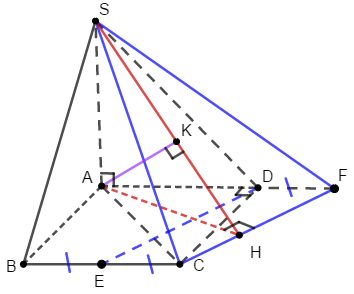
Bước 1:
Kẻ CF||DE ( F thuộc AD).
=> DE||(SCF)
Bước 2:
=>d(DE,SC)=d(DE,(SCF))=d(D,(SCF)).
ECFD là hình bình hành nên
\(\begin{array}{l}DF = EC = \dfrac{{AD}}{2} \Rightarrow \dfrac{{AF}}{{DF}} = 3\\ \Rightarrow d\left( {D,\left( {SCF} \right)} \right) = \dfrac{1}{3}d\left( {A,\left( {SCF} \right)} \right)\end{array}\).
Bước 3:
Kẻ \(AH \bot CF;AK \bot SH\)
\(\begin{array}{l}\left. \begin{array}{l} \Rightarrow CF \bot AH\\CF \bot SA\end{array} \right\} \Rightarrow CF \bot \left( {SAH} \right)\\ \Rightarrow CF \bot AK \Rightarrow AK \bot \left( {SCF} \right)\\ \Rightarrow d\left( {A,\left( {SCF} \right)} \right) = AK\end{array}\)
Bước 4:
\(\begin{array}{l}\tan \widehat {HFA} = \tan \widehat {CFD} = \dfrac{{DC}}{{DF}} = 2\\ \Rightarrow AH = 2HF\\ \Rightarrow A{H^2} + \dfrac{{A{H^2}}}{4} = A{F^2} = {\left( {\dfrac{3}{2}.a\sqrt 2 } \right)^2}\\ \Rightarrow \dfrac{5}{4}A{H^2} = \dfrac{{9{a^2}}}{2} \Rightarrow A{H^2} = \dfrac{{18{a^2}}}{5}\\\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{S{A^2}}}\\ = \dfrac{5}{{18{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{19}}{{36{a^2}}}\\ \Rightarrow AK = \dfrac{{6a}}{{\sqrt {19} }}\\ \Rightarrow d\left( {SC,DE} \right) = \dfrac{{2a}}{{\sqrt {19} }}\end{array}\)
Hướng dẫn giải:
Bước 1: Xác định mặt phẳng (P) qua SC và song song với DE.
\(d\left( {SC,DE} \right) = d\left( {D,\left( P \right)} \right)\)
Bước 2: Tìm mối quan hệ \(d\left( {A,\left( P \right)} \right)\) và \(d\left( {D,\left( P \right)} \right)\).
Bước 3: Tìm hình chiếu của A lên (P).
Bước 4: Tính \(d\left( {A,\left( P \right)} \right)\) từ đó tính \(d\left( {D,\left( P \right)} \right)\).
