Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a,BC = a\sqrt 3 \). Hình chiếu vuông góc của \(S\) trên mặt đáy là trung điểm \(H\) của cạnh \(AC\). Biết \(SB = a\sqrt 2 \). Tính theo \(a\) khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAB} \right)\)?
Trả lời bởi giáo viên
Đáp án đúng: b
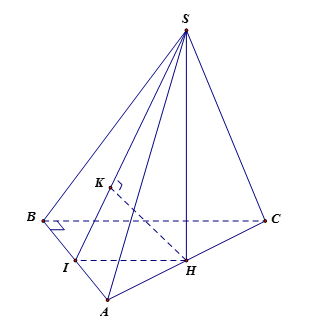
Để tính khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAB} \right)\), ta xác định hình chiếu vuông góc của \(H\) trên mặt phẳng \(\left( {SAB} \right)\) qua các bước sau:
- Dựng \(HI \bot AB\) với \(I \in AB\), chứng minh được \(AB \bot \left( {SIH} \right)\) và \(\left( {SIH} \right) \bot \left( {SAB} \right) = SI\).
- Dựng \(K\) là hình chiếu vuông góc của \(H\) trên \(SI\), ta chứng minh được \(SK \bot \left( {SAB} \right)\).
Vậy \(d\left( {H,\left( {SAB} \right)} \right) = HK\).
Do \(HI/{\kern 1pt} /BC\) nên dễ dàng chỉ ra được \(I\) là trung điểm của \(AB\) và \(IH = \dfrac{{BC}}{2} = \dfrac{{a\sqrt 3 }}{2}\), \(IA = IB = \dfrac{{AB}}{2} = \dfrac{a}{2}\).
Ta có \(AB \bot SI\) nên \(SI = \sqrt {S{B^2} - I{B^2}} = \sqrt {2{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 7 }}{2}\).
Do \(SH \bot IH\) nên xét tam giác vuông \(SIH\) có:
\(SH = \sqrt {S{I^2} - I{H^2}} = \sqrt {\dfrac{{7{a^2}}}{4} - \dfrac{{3{a^2}}}{4}} = a\) ; \(HK = \dfrac{{SH.HI}}{{SI}} = \dfrac{{a.\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{{a\sqrt 7 }}{2}}} = \dfrac{{a\sqrt {21} }}{7}\).
Do vậy, ta có \(d\left( {H,\left( {SAB} \right)} \right) = \dfrac{{a\sqrt {21} }}{7}\).
Hướng dẫn giải:
- Dựng đoạn vuông góc kẻ từ \(H\) đến mặt phẳng \(\left( {SAB} \right)\).
- Tính toán dựa vào kiến thức hình học đã biết
