Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và $\widehat {BAD} = 60^\circ $. Hình chiếu vuông góc của \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) trùng với trọng tâm của tam giác \(ABC\). Góc giữa mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng \(60^\circ \). Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
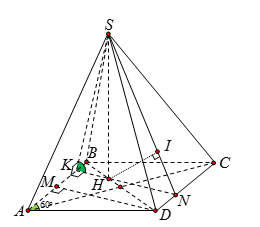
Gọi \(H\) là trọng tâm tam giác \(ABC\), \(M\) là trung điểm \(AB\)
Ta có tam giác \(ABD\) là tam giác đều\( \Rightarrow DM = \dfrac{{a\sqrt 3 }}{2}\) và \(BD = a\)
Kẻ \(HK \bot AB\) \( \Rightarrow HK\,{\rm{//}}\,DM\) \( \Rightarrow \dfrac{{HK}}{{DM}} = \dfrac{{BH}}{{BD}}\) \( \Rightarrow HK = DM.\dfrac{{BH}}{{BD}} = \dfrac{1}{3}DM = \dfrac{{a\sqrt 3 }}{6}\)
\(\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\), \(AB \bot HK\), \(AB \bot SK\) (định lí ba đường vuông góc)
\( \Rightarrow \left( {\widehat {\left( {SAB} \right),\,\left( {ABCD} \right)}} \right) = \widehat {SKH}\)
Tam giác \(SHK\) vuông tại \(H\) có \(SH = HK.\tan 60^\circ = \dfrac{a}{2}\).
Gọi \(N\) là giao điểm của \(HK\) và \(CD\)
Ta có \(\left\{ \begin{array}{l}HN \bot CD\\SH \bot CD\end{array} \right. \Rightarrow CD \bot \left( {SHN} \right)\); \(CD \subset \left( {SCD} \right)\) \( \Rightarrow \left( {SCD} \right) \bot \left( {SHN} \right)\) và \(\left( {SHN} \right) \cap \left( {SCD} \right) = SN\)
Trong mặt phẳng \(\left( {SHN} \right)\) kẻ \(HI \bot SN\) thì \(HI \bot \left( {SCD} \right)\) \( \Rightarrow HI = d\left( {H,\,\left( {SCD} \right)} \right)\)
Tam giác \(SHN\) vuông tại \(H\) có \(\dfrac{1}{{H{I^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{N^2}}}\), với \(HN = \dfrac{2}{3}DM = \dfrac{a}{{\sqrt 3 }}\)
\( \Rightarrow HI = \dfrac{{a\sqrt 7 }}{7}\)
Lại có \(\dfrac{{BD}}{{HD}} = \dfrac{3}{2}\) $ \Rightarrow d\left( {B,\,\left( {SCD} \right)} \right) = \dfrac{3}{2}d\left( {H,\,\left( {SCD} \right)} \right)$
Vậy \(d\left( {B,\,\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 7 }}{{14}}\).
Hướng dẫn giải:
Sử dụng mối quan hệ khoảng cách từ các điểm đến cùng một mặt phẳng để tính khoảng cách.
