Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = 3a\), \(BC = 4a\), mặt phẳng \(\left( {SBC} \right)\) vuông góc với mặt phẳng \(\left( {ABC} \right)\). Biết \(SB = 2\sqrt 3 a\), \(\widehat {SBC} = 30^\circ \). Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: b
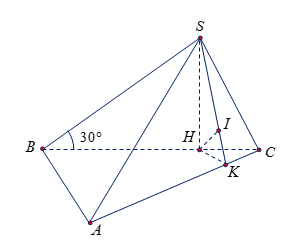
Trong \(\left( {SBC} \right)\), kẻ \(SH \bot BC\) tại $H$. Ta có nên \(SH \bot \left( {ABC} \right)\).
Ta có \(\Delta SBH\) vuông tại \(H\) có \(SH = SB.\sin 30^\circ = a\sqrt 3 \); \(BH = SB.\cos 30^\circ = 3a\);
\(HC = BC - BH = a\).
Khi đó \(BH = 4HC\) nên \(d\left( {B,\,\left( {SAC} \right)} \right) = 4d\left( {H,\,\left( {SAC} \right)} \right)\)
Trong \(\left( {ABC} \right)\), kẻ \(HK \bot AC\); trong \(\left( {SHK} \right)\), kẻ \(HI \bot SK\).
Ta có \(SH \bot AC\) nên \(AC \bot \left( {SHK} \right)\) suy ra \(AC \bot HI\) hay \(HI = d\left( {H,\,\left( {SAC} \right)} \right)\).
nên \(\dfrac{{HK}}{{AB}} = \dfrac{{CH}}{{CA}}\)\( \Rightarrow HK = \dfrac{{CH.AB}}{{\sqrt {A{B^2} + B{C^2}} }} = \dfrac{{3a}}{5}\).
Tam giác \(SHK\) vuông tại \(H\) có \(\dfrac{1}{{H{I^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{K^2}}}\)\( \Rightarrow HI = \dfrac{{SH.HK}}{{\sqrt {S{H^2} + H{K^2}} }} = \dfrac{{3\sqrt 7 a}}{{14}}\).
Vậy \(d\left( {B,\,\left( {SAC} \right)} \right) = \dfrac{{6\sqrt 7 a}}{7}\).
Hướng dẫn giải:
Sử dụng mối quan hệ tỉ lệ giữa các khoảng cách từ các điểm đến cùng một mặt phẳng tính khoảng cách.
