Câu hỏi:
2 năm trước
Cho hình lăng trụ $ABC.A'B'C'$ có mặt đáy $ABC$ là tam giác đều cạnh $AB = 2a$. Hình chiếu vuông góc của $A'$ lên mặt phẳng $\left( {ABC} \right)$ trùng với trung điểm $H$ của $AB$. Biết góc giữa cạnh bên và mặt đáy bằng $60^\circ $. Tính theo $a$ khoảng cách $h$ từ điểm $B$ đến mặt phẳng $\left( {ACC'A'} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: b
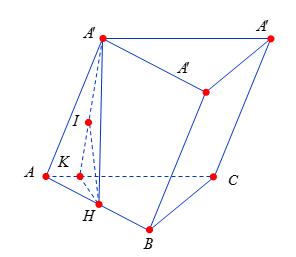
Ta có: $\widehat {A'AH} = 60^\circ \Rightarrow A'H = AH.\tan 60^\circ = a\sqrt 3 $.
Kẻ$HK \bot AC,HI \bot A'K \Rightarrow HK = AH.\sin 60^\circ = \dfrac{{a\sqrt 3 }}{2}$ (hình vẽ).
Ta có $\dfrac{1}{{I{H^2}}} = \dfrac{1}{{H{{A'}^2}}} + \dfrac{1}{{H{K^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{4}{{3{a^2}}} \Rightarrow IH = \dfrac{{\sqrt {15} a}}{5}$.
$d\left( {B,\left( {ACC'A'} \right)} \right) = 2d\left( {H,ACC'A'} \right) = 2HI = \dfrac{{2\sqrt {15} a}}{5}$.
Hướng dẫn giải:
- Xác định góc \({60^0}\).
- Sử dụng mối quan hệ khoảng cách từ các điểm đến mặt phẳng và tính toán dựa vào các kiến thức hình học đã biết.
