Trong mặt phẳng tọa độ $Oxy$, cho hình chữ nhật \(OMNP\) với \(M\left( {0;10} \right)\), \(N\left( {100;10} \right)\), \(P\left( {100;0} \right)\) Gọi S là tập hợp tất cả các điểm \(A\left( {x;y} \right)\) với \(x\), \(y \in \mathbb{Z}\) nằm bên trong kể cả trên cạnh của hình chữ nhật \(OMNP\). Lấy ngẫu nhiên 1 điểm \(A\left( {x;y} \right) \in S\). Tính xác suất để \(x + y \le 90\).

Cách 1: Tập hợp \(S\) gồm có \(11.101 = 1111\) điểm.

Ta xét \(S' = \left\{ {\left( {x;y} \right):x + y > 90} \right\}\)với \(0 \le x \le 100\) và \(0 \le y \le 10\)

• Khi \(y = 0\) \( \Rightarrow \)\(x > 90\) \( \Rightarrow \)\(x = \overline {91;100} \) \( \Rightarrow \) có \(10\) giá trị của \(x\)
• Khi \(y = 1\) \( \Rightarrow \)\(x > 89\) \( \Rightarrow \)\(x = \overline {90;100} \) \( \Rightarrow \) có \(11\) giá trị của \(x\)
• Khi \(y = 10\) \( \Rightarrow \)\(x > 90\) \( \Rightarrow \)\(x = \overline {91;100} \) \( \Rightarrow \) có \(20\) giá trị của \(x\)

Như vậy \(S'\) có 165 phần tử. Vậy xác suất cần tìm là \(\dfrac{{1111 - 165}}{{1111}} = \dfrac{{86}}{{101}}\).

Cách 2:

Nhận thấy các điểm cần tìm nằm trên các đường thẳng \(y = m\), \(m = \overline {0;10} \).

Dễ thấy trên các đường thẳng \(y = 0\), \(y = 1\), \(y = 2...\), \(y = 10\) có lần lượt \(91\), \(90\), \(89...\),\(81\) điểm.

Vậy xác suất cần tìm là \(p\left( A \right) = \dfrac{{91 + 90 + ... + 81}}{{11.101}} = \dfrac{{86}}{{101}}\).

Cách 3:

\(n\left( \Omega  \right) = 11.101 = 1111\).

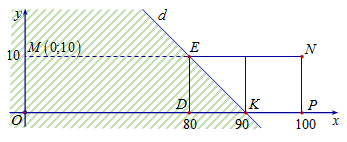
Ta thấy $x + y \le 90$ có miền nghiệm là nửa mặt phẳng có bờ là đường thẳng $d$ chứa điểm $O$.

Số điểm thuôc hcn $ENPD$ là $21.11 = 231$

Số điểm thuộc $\Delta EDK$ tính cả cạnh $EK$ là $55 + 11 = 66$

Suy ra $x + y > 90$ có $231 - 66 = 165$ điểm và $x + y \le 90$ có \(1111 - 165 = 946\)

\(P\left( A \right) = \dfrac{{946}}{{1111}} = \dfrac{{86}}{{101}}\)