Bài toán thiết diện của hình chóp

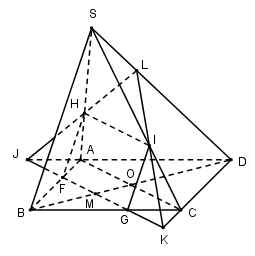
Gọi $O = AC \cap BD$

Trường hợp 1: $M$  nằm giữa $O$  và $B$ .

Trong $\left( {ABCD} \right)$  qua $M$  kẻ $FG//AC\left( {F \in AB,G \in BC} \right)$

Trong $\left( {SAB} \right)$  qua $F$  kẻ  $FH//SB\left( {H \in SA} \right)$. 

$\Rightarrow mp\left( \alpha  \right)$ là $\left( {FHG} \right)$ .

Ta có: $\left( \alpha  \right) \cap \left( {ABCD} \right) = FG,\left( \alpha  \right) \cap \left( {SAB} \right) = FH.$

Ta có: $mp\left( \alpha  \right)$ và $\left( {SAC} \right)$  có $H$  chung.

$\begin{array}{l}\left( \alpha  \right) \supset FG\\\left( {SAC} \right) \supset AC\\FG//AC\end{array}$

$\Rightarrow$ Qua $H$  kẻ $HI//AC\left( {I \in SC} \right),mp\left( \alpha  \right) \cap \left( {SAC} \right) = HI,mp\left( \alpha  \right) \cap \left( {SBC} \right) = GI$

Trong $\left( {ABCD} \right)$  kéo dài $FG$  cắt $CD$  và $AD$  lần lượt tại $K$  và $J\left( {K \in CD,J \in AD} \right)$.

Trong $\left( {SCD} \right)$  gọi $L = KI \cap SD \Rightarrow \left( \alpha  \right) \cap \left( {SCD} \right) = IL,\left( \alpha  \right) \cap \left( {SAD} \right) = HL.$

Vậy thiết diện của hình chóp cắt bởi $mp\left( \alpha  \right)$ là ngũ giác $HFGIL$ .

Trường hợp 2: $M$  nằm giữa $O$  và $D$ .

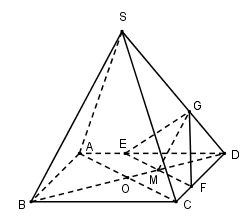
Trong $\left( {ABCD} \right)$  qua $M$  kẻ $EF//AC\left( {E \in AD,F \in CD} \right)$.

Trong $\left( {SBD} \right)$  qua $M$  kẻ $MG//SB\left( {G \in SD} \right).$

$\Rightarrow mp\left( \alpha  \right)$ là $\left( {EFG} \right)$  và $EFG$  cũng chính là thiết diện của hình chóp khi cắt bởi $mp\left( \alpha  \right)$.

Vậy thiết diện là tam giác.

Tóm lại, tùy vào vị trí của điểm $M$ trên đoạn $BD$ , thiết diện của hình chóp cắt bởi $mp\left( \alpha  \right)$ có thể là tam giác hoặc ngũ giác.

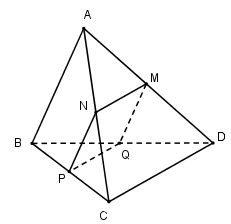
Giả sử $\left( \alpha  \right)$ cắt các cạnh $AD,AC,CB,BD$  theo thứ tự tại $M,N,P,Q$.

$\left\{ \begin{array}{l}CD//\left( \alpha  \right),CD \subset \left( {ACD} \right)\\M \in \left( \alpha  \right) \cap \left( {ACD} \right)\end{array} \right. \Rightarrow \left( \alpha  \right) \cap \left( {ACD} \right) = MN//CD\,\,\left( {N \in AC} \right)$

Tương tự $\left( \alpha  \right) \cap \left( {BCD} \right) = PQ//CD\,\,\left( {Q \in BD} \right).$

Khi đó: $\left( \alpha  \right) \cap \left( {ABD} \right) = MQ//AB,\left( \alpha  \right) \cap \left( {ABC} \right) = NP//AB.$

Hình bình hành $MNPQ$  là thiết diện của hình chóp cắt bởi $mp\left( \alpha  \right)$.

Theo định lí Ta-let ta có:

$\dfrac{{NP}}{{AB}} = \dfrac{{CN}}{{CA}} \Rightarrow NP = \dfrac{a}{c}CN,\,\,\dfrac{{MN}}{{CD}} = \dfrac{{AN}}{{AC}} \Rightarrow MN = \dfrac{a}{b}AN.$

Để MNPQ là hình thoi thì $MN = NP \Rightarrow CN = AN$ hay $N$  là trung điểm của $AC$ . Từ đó suy ra $M,P,Q$ lần lượt là trung điểm của $AD,BC,BD$ .

Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}D{N^2} = \dfrac{{A{D^2} + D{C^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4}\\B{N^2} = \dfrac{{A{B^2} + B{C^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4}\end{array} \right.\\ \Rightarrow DN = BN\end{array}$

$\Rightarrow \Delta NBD$ cân tại $N$ . Lại có $Q$ là trung điểm của $BD$ nên $NQ \bot BD.$

Do đó ta có: $N{Q^2} = N{B^2} - B{Q^2} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4} - \dfrac{{{c^2}}}{4} = \dfrac{{{b^2} + {a^2} - {c^2}}}{2}$

Tương tự ta tính được $M{P^2} = \dfrac{{{c^2} + {a^2} - {b^2}}}{2}.$

Vậy ${S_{MNPQ}} = \dfrac{1}{2}MP.NQ = \dfrac{1}{2}\sqrt {\dfrac{{{b^2} + {a^2} - {c^2}}}{2}.\dfrac{{{c^2} + {a^2} - {b^2}}}{2}}  = \dfrac{1}{4}\sqrt {\left( {{b^2} + {a^2} - {c^2}} \right)\left( {{c^2} + {a^2} - {b^2}} \right)}$ .

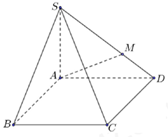
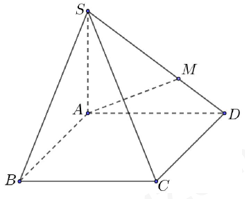
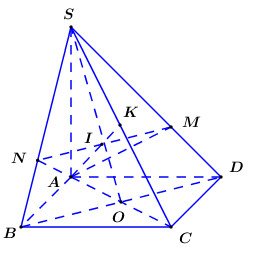
Gọi mặt phẳng chứa $AM$ và song song với $BD$ là $\left( \alpha  \right)$.

Trong $\left( {SBD} \right)$ kẻ $MN//BD\,\,\left( {N \in SB} \right)$, khi đó ta có $\left( \alpha  \right) \equiv \left( {AMN} \right)$.

Gọi $O = AC \cap BD$, trong $\left( {SBD} \right)$ gọi $\left\{ I \right\} = MN \cap SO$, trong $\left( {SAC} \right)$ gọi $K = AI \cap SC$ ta có:

$\left\{ \begin{array}{l}K \in AI \subset \left( {AMN} \right)\\K \in SC\end{array} \right.$$\Rightarrow K = \left( {AMN} \right) \cap SC$ hay $K = \left( \alpha  \right) \cap SC$.

Áp dụng định lí Talets ta có $\dfrac{{SI}}{{SO}} = \dfrac{{SM}}{{SD}} = \dfrac{2}{3}$.

$\Rightarrow \dfrac{{IS}}{{IO}}=2$

Ta có: O là trung điểm của AC nên $\dfrac{{AO}}{{AC}}=\dfrac{1}{2}$

Áp dụng định lí Menelaus trong tam giác $SOC$, cát tuyến $AIK$ ta có:

$\dfrac{{IS}}{{IO}}.\dfrac{{AO}}{{AC}}.\dfrac{{KC}}{{KS}} = 1 \Leftrightarrow 2.\dfrac{1}{2}.\dfrac{{KC}}{{KS}} = 1 \Leftrightarrow \dfrac{{KC}}{{KS}} = 1$ $\Rightarrow \dfrac{{SK}}{{SC}} = \dfrac{1}{2}$.