Cho tứ diện $ABCD$ có $AB = CD = a,BC = AD = b,AC = BD = c$. Mặt phẳng \(\left( \alpha  \right)\) song song với $AB$  và $CD$ cắt các cạnh của tứ diện theo một thiết diện là hình thoi. Diện tích thiết diện là:

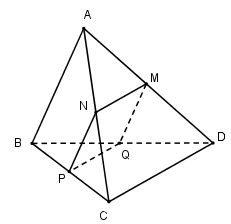
Giả sử \(\left( \alpha  \right)\) cắt các cạnh $AD,AC,CB,BD$  theo thứ tự tại $M,N,P,Q$.

\(\left\{ \begin{array}{l}CD//\left( \alpha  \right),CD \subset \left( {ACD} \right)\\M \in \left( \alpha  \right) \cap \left( {ACD} \right)\end{array} \right. \Rightarrow \left( \alpha  \right) \cap \left( {ACD} \right) = MN//CD\,\,\left( {N \in AC} \right)\)

Tương tự \(\left( \alpha  \right) \cap \left( {BCD} \right) = PQ//CD\,\,\left( {Q \in BD} \right).\)

Khi đó: \(\left( \alpha  \right) \cap \left( {ABD} \right) = MQ//AB,\left( \alpha  \right) \cap \left( {ABC} \right) = NP//AB.\)

Hình bình hành $MNPQ$  là thiết diện của hình chóp cắt bởi \(mp\left( \alpha  \right)\).

Theo định lí Ta-let ta có:

\(\dfrac{{NP}}{{AB}} = \dfrac{{CN}}{{CA}} \Rightarrow NP = \dfrac{a}{c}CN,\,\,\dfrac{{MN}}{{CD}} = \dfrac{{AN}}{{AC}} \Rightarrow MN = \dfrac{a}{b}AN.\)

Để MNPQ là hình thoi thì \(MN = NP \Rightarrow CN = AN\) hay $N$  là trung điểm của $AC$ . Từ đó suy ra $M,P,Q$ lần lượt là trung điểm của $AD,BC,BD$ .

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}D{N^2} = \dfrac{{A{D^2} + D{C^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4}\\B{N^2} = \dfrac{{A{B^2} + B{C^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4}\end{array} \right.\\ \Rightarrow DN = BN\end{array}\)

\( \Rightarrow \Delta NBD\) cân tại $N$ . Lại có $Q$ là trung điểm của $BD$ nên \(NQ \bot BD.\)

Do đó ta có: \(N{Q^2} = N{B^2} - B{Q^2} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4} - \dfrac{{{c^2}}}{4} = \dfrac{{{b^2} + {a^2} - {c^2}}}{2}\)

Tương tự ta tính được \(M{P^2} = \dfrac{{{c^2} + {a^2} - {b^2}}}{2}.\)

Vậy \({S_{MNPQ}} = \dfrac{1}{2}MP.NQ = \dfrac{1}{2}\sqrt {\dfrac{{{b^2} + {a^2} - {c^2}}}{2}.\dfrac{{{c^2} + {a^2} - {b^2}}}{2}}  = \dfrac{1}{4}\sqrt {\left( {{b^2} + {a^2} - {c^2}} \right)\left( {{c^2} + {a^2} - {b^2}} \right)} \) .