Cho hình chóp $S.ABCD$ có đáy $ABCD$  là hình bình hành, $M$  là một điểm nằm trên đoạn đường chéo $BD$ . Thiết diện của hình chóp cắt bởi \(mp\left( \alpha  \right)\) đi qua $M$  và song song với $AC$  và $SB$  có thể là những hình gì?

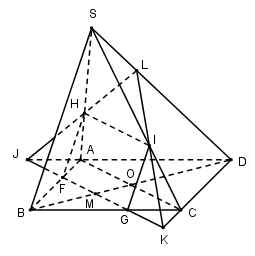
Gọi \(O = AC \cap BD\)

Trường hợp 1: $M$  nằm giữa $O$  và $B$ .

Trong $\left( {ABCD} \right)$  qua $M$  kẻ \(FG//AC\left( {F \in AB,G \in BC} \right)\)

Trong $\left( {SAB} \right)$  qua $F$  kẻ  \(FH//SB\left( {H \in SA} \right)\). 

\( \Rightarrow mp\left( \alpha  \right)\) là $\left( {FHG} \right)$ .

Ta có: \(\left( \alpha  \right) \cap \left( {ABCD} \right) = FG,\left( \alpha  \right) \cap \left( {SAB} \right) = FH.\)

Ta có: \(mp\left( \alpha  \right)\) và $\left( {SAC} \right)$  có $H$  chung.

\(\begin{array}{l}\left( \alpha  \right) \supset FG\\\left( {SAC} \right) \supset AC\\FG//AC\end{array}\)

\( \Rightarrow \) Qua $H$  kẻ \(HI//AC\left( {I \in SC} \right),mp\left( \alpha  \right) \cap \left( {SAC} \right) = HI,mp\left( \alpha  \right) \cap \left( {SBC} \right) = GI\)

Trong $\left( {ABCD} \right)$  kéo dài $FG$  cắt $CD$  và $AD$  lần lượt tại $K$  và \(J\left( {K \in CD,J \in AD} \right)\).

Trong $\left( {SCD} \right)$  gọi \(L = KI \cap SD \Rightarrow \left( \alpha  \right) \cap \left( {SCD} \right) = IL,\left( \alpha  \right) \cap \left( {SAD} \right) = HL.\)

Vậy thiết diện của hình chóp cắt bởi \(mp\left( \alpha  \right)\) là ngũ giác $HFGIL$ .

Trường hợp 2: $M$  nằm giữa $O$  và $D$ .

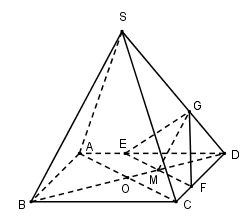
Trong $\left( {ABCD} \right)$  qua $M$  kẻ \(EF//AC\left( {E \in AD,F \in CD} \right)\).

Trong $\left( {SBD} \right)$  qua $M$  kẻ \(MG//SB\left( {G \in SD} \right).\)

\( \Rightarrow mp\left( \alpha  \right)\) là $\left( {EFG} \right)$  và $EFG$  cũng chính là thiết diện của hình chóp khi cắt bởi \(mp\left( \alpha  \right)\).

Vậy thiết diện là tam giác.

Tóm lại, tùy vào vị trí của điểm $M$ trên đoạn $BD$ , thiết diện của hình chóp cắt bởi \(mp\left( \alpha  \right)\) có thể là tam giác hoặc ngũ giác.