Cho tứ diện $ABCD$  có \(AB = a,CD = b,AB \bot CD\). Gọi $I$  và $J$  lần lượt là trung điểm của $AB$  và $CD$ . Mặt phẳng \(\left( \alpha  \right)\) qua $M$  nằm trên đoạn $IJ$  và song song với $AB$ và $CD$. Giao tuyến của mặt phẳng \(\left( \alpha  \right)\) và hình chóp có diện tích bằng bao nhiêu, biết $IJ = 3IM$

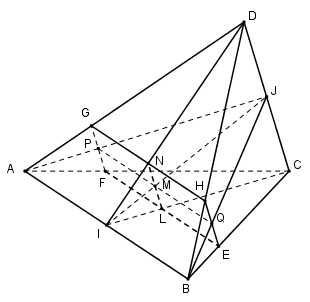
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha  \right) \cap \left( {ICD} \right)\\CD\parallel \left( \alpha  \right)\\CD \subset \left( {ICD} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha  \right)\) và $\left( {ICD} \right)$ là đường thẳng qua $M$  và song song với $CD$  cắt $IC$  tại $L$  và cắt $ID$  tại $N$.

Tương tự \(\left\{ \begin{array}{l}M \in \left( \alpha  \right) \cap \left( {JAB} \right)\\AB\parallel \left( \alpha  \right)\\AB \subset \left( {JAB} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha  \right)\) và $\left( {JAB} \right)$ là đường thẳng qua $M$ và song song $AB$  cắt $JA$  tại $P$  và cắt $JB$  tại $Q$.

Ta có: \(\left\{ \begin{array}{l}L \in \left( \alpha  \right) \cap \left( {ABC} \right)\\AB\parallel \left( \alpha  \right)\\AB \subset \left( {ABC} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha  \right)\) với $\left( {ABC} \right)$ là đường thẳng qua $L$ song song với $AB$ cắt $BC$ tại $E$ và cắt $AC$  tại $F$ . Do đó $EF//AB{\rm{ }}\left( 1 \right)$

Tương tự \(\left\{ \begin{array}{l}N \in \left( \alpha  \right) \cap \left( {ABD} \right)\\AB\parallel \left( \alpha  \right)\\AB \subset \left( {ABD} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha  \right)\)và $\left( {ABD} \right)$  là đường thẳng qua $N$  song song với $AB$  cắt $BD$  tại $H$  và cắt $AD$  tại $G$ .

Do đó $HG//AB\left( 2 \right)$ .

Từ (1) và (2) suy ra EF // HG // AB (*)

Ta có: $\left\{ \begin{array}{l}FG = \left( \alpha  \right) \cap \left( {ACD} \right)\\CD\parallel \left( \alpha  \right)\\CD \subset \left( {ACD} \right)\end{array} \right. \Rightarrow FG\parallel CD\,\,\,\left( 3 \right)$.

Tương tự \(\left\{ \begin{array}{l}EH = \left( \alpha  \right) \cap \left( {BCD} \right)\\CD\parallel \left( \alpha  \right)\\CD \subset \left( {BCD} \right)\end{array} \right. \Rightarrow EH\parallel CD\,\,\left( 4 \right).\)

Từ (*) và (**) suy ra $EFGH$  là hình bình hành.

Mà \(AB \bot CD \Rightarrow EF \bot FG.\) Vậy thiết diện $EFGH$ là hình chữ nhật

\( \Rightarrow {S_{EFGH}} = EF.FG = PQ.LN.\)

Trong tam giác $JAB$, ta có \(\dfrac{{PQ}}{{AB}} = \dfrac{{JM}}{{JI}} = \dfrac{2}{3} \Rightarrow PQ = \dfrac{{2AB}}{3} = \dfrac{{2a}}{3}.\)

Trong tam giác $ICD$  ta có \(\dfrac{{LN}}{{CD}} = \dfrac{{IM}}{{IJ}} = \dfrac{1}{3} \Rightarrow LN = \dfrac{{CD}}{3} = \dfrac{b}{3}.\)

Vậy diện tích thiết diện là: \({S_{EFGH}} = \dfrac{{2a}}{3}.\dfrac{b}{3} = \dfrac{{2ab}}{9}.\)