Câu hỏi:
2 năm trước
Cho tứ diện đều $ABCD$ cạnh $a$ . Gọi $M$ và $P$ lần lượt là hai điểm di động trên các cạnh $AD$ và $BC$ sao cho $MA = PC = x\left( {0 < x < \dfrac{a}{2}} \right)$ . Mặt phẳng \(\left( \alpha \right)\) đi qua $MP$ song song với $CD$ cắt tứ diện theo một thiết diện là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: d
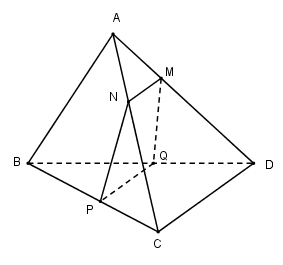
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ACD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {ACD} \right)\end{array} \right.\)
Suy ra \(\left( \alpha \right) \cap \left( {ACD} \right) = MN\parallel CD\) với \(N \in AC\).
Tương tự \(\left( \alpha \right) \cap \left( {BCD} \right) = PQ\parallel CD\) với \(Q \in BD.\)
Vì $MN//CD//PQ$ nên thiết diện $MNPQ$ là hình thang.
Ta có $DQ = CP = x,DM = a-x$.
Áp dụng định lí Cosin trong tam giác $DMQ$ ta có:
\(MQ = \sqrt {D{M^2} + D{Q^2} - 2DM.DQ.cos60} = \sqrt {3{x^2} - 3ax + {a^2}} .\)
Tương tự ta cũng tính được \(NP = \sqrt {3{x^2} - 3ax + {a^2}} .\)
Suy ra $MQ = NP$ .
Mặt khác ta có
\(\begin{array}{l}MN = x < \dfrac{a}{2};PQ = a - x > \dfrac{a}{2}\\ \Rightarrow MN \ne PQ\end{array}\)
\( \Rightarrow MNPQ\) không là hình bình hành
Vậy thiết diện $MNPQ$ là hình thang cân.
Hướng dẫn giải:
- Đưa về cùng mặt phẳng.
- Sử dụng các tính chất về đường cao, đường trung tuyến trong tam giác cân.
- Vận dụng các dấu hiệu nhận biết một số tứ giác đặc biệt.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
